Araştırma çalışması "İkinci dereceden denklemleri çözmenin 10 yolu". İkinci dereceden denklemleri çözmenin yolları Kareyi çözmenin 10 yolu

Eğitim ve Bilim Bölümü

Kemerovo bölgesi

GOU DPT "Mariinsky Tarım Koleji"

ÇÖZÜMÜN 10 YOLU

KARE DENKLEMLER

eksen ²+in+c=0

İş tamamlandı:

kral inancı,

grup öğrencisi 161

uzmanlık 260807 "Yemekhane ürünleri teknolojisi"

Süpervizör:

Matveeva Olga Vasilyevna,

Matematik öğretmeni

Mariinsk, 2013

I.Giriş

II. Olay tarihi ikinci dereceden denklemler

2. Eski Babil'de ikinci dereceden denklemler.

3. Avrupa'da ikinci dereceden denklemlerXIII – XVII yüzyıllar

III. İkinci dereceden denklemleri çözmenin yolları

3. İkinci dereceden denklemleri çözmenin özel durumları:

a) katsayı a - çok küçük,

b) katsayı İle birlikte - çok küçük.

4. Vieta teoremini kullanarak denklemlerin çözümü.

6. Denklemlerin "aktarım" yöntemiyle çözümü.

9. Bir nomogram kullanarak ikinci dereceden denklemleri çözme.

IV. Çözüm

V. Edebiyat

I.GİRİŞ

« Bir cebir öğrencisi için aynı problemi üç ya da dört farklı problemi çözmektense üç farklı şekilde çözmek genellikle daha faydalıdır. Bir problemi farklı yöntemlerle çözerek hangisinin daha kısa ve verimli olduğunu karşılaştırma yaparak bulmak mümkündür. Tecrübe böyle yapılır."

W. Sawyer

İkinci dereceden denklemler, cebirin görkemli yapısının dayandığı temeldir. İkinci dereceden denklemler, çeşitli çözümlerin çözümünde yaygın olarak kullanılmaktadır.trigonometrik, üstel, logaritmik, irrasyonel, aşkın denklemler ve eşitsizlikler, Büyük bir sayı farklı şekiller görevler.

Denklemler teorisi, genel olarak cebir ve matematikte önde gelen bir yer tutar. Denklemler teorisinin gücü, sadece doğa yasalarının bilgisi için teorik öneme sahip olması değil, aynı zamanda pratik amaçlara hizmet etmesidir. Hayattaki problemlerin çoğu çözmek için gelir Çeşitli türler denklemler ve daha sıklıkla bunlar ikinci dereceden bir formun denklemleridir.

İkinci dereceden denklem, hem formüller hem de temel işlevler kullanılarak çözülebilen büyük ve önemli bir denklem sınıfıdır.

AT okul kursu matematik, birkaç tür ikinci dereceden denklemle tanışırız ve standart formülleri kullanarak çözümü yaparız. Aynı zamanda, modern bilimsel ve metodolojik araştırmalar, çeşitli yöntem ve tekniklerin kullanılmasının, ikinci dereceden denklemlere yönelik çözümlerin incelenmesinin verimliliğini ve kalitesini önemli ölçüde artırabileceğini göstermektedir.

Bu nedenle, ikinci dereceden denklemleri çözmenin çeşitli yollarını incelemeye ihtiyaç vardır.

Yukarıdakilerin tümü tanımlaralaka Araştırma konuları.

Sorun araştırma, ikinci dereceden denklemleri çözmenin standart olmayan yolları da dahil olmak üzere çeşitli konuları ele almaktır.

Hedef iş okumaktır teorik temeller ve ikinci dereceden denklemlerin çözümündeki uygulamaları.

Ders araştırma: ikinci dereceden denklemler ve çözümleri.

Görevler:

Bu konuyla ilgili literatürün bir analizini yapın.

İkinci dereceden denklemlerin gelişim tarihini incelemek.

Standart olmayanlar da dahil olmak üzere ikinci dereceden denklemleri çözmenin çeşitli yollarını incelemek ve materyali pratikte test etmek.

II. İKİNCİ DENKLEMLERİN KÖKENİNİN TARİHÇESİ

1. Hindistan'da ikinci dereceden denklemler.

İkinci dereceden denklemler için problemler, 499 yılında Hintli matematikçi ve astronom Aryabhata tarafından derlenen astronomik traktör "Aryabhattiam" da bulunur. Başka bir Hintli bilgin - Brahmagupta (VIIc.) özetlenen Genel kural ikinci dereceden denklemlerin çözümleri. Brahmagupta'nın kuralı esasen modern olanla örtüşür.

Eski Hindistan'da, zor sorunları çözmede halka açık yarışmalar yaygındı. Eski Hint kitaplarından birinde, bu tür yarışmalar hakkında şöyle söylenir: “Güneş, parlaklığıyla yıldızları gölgede bırakırken, bilim adamı Cebirsel problemleri önererek ve çözerek, halka açık toplantılarda bir başkasının ihtişamını gölgede bırakın. Görevler genellikle şiirsel bir biçimde giyinirdi.

İşte ünlü Hintli matematikçinin problemlerinden biriXII Bhaskara'da.

Maymun sürüsü

Güç yemiş, eğlenmiş.

Sekizinci bölümün karesi

Çayırda eğlenmek

Ve on iki asma tarafından

Atlamaya başladılar, asılı kaldılar ..

kaç maymun vardı

Bana bu sürüde mi söylüyorsun?

Bhaskara'nın çözümü, ikinci dereceden denklemlerin köklerinin iki değerliliğini bildiğini gösterir.

x 2 - 64 = - 768,

x 2 - 64x +32 2 \u003d - 768 + 1024,

(x - 32) 2 \u003d 256,

x 1 = 16, x 2 = 48

2. Eski Babil'de İkinci Dereceden Denklemler.

Babilliler, MÖ 2000 civarında ikinci dereceden denklemleri nasıl çözeceklerini biliyorlardı. modern uygulama cebirsel gösterim, çivi yazısı metinlerinde eksik olanlara ek olarak, örneğin tam denklemler olduğunu söyleyebiliriz.

Babil metinlerinde belirtilen bu denklemleri çözme kuralı esasen modern olanla örtüşmektedir, ancak Babillilerin bu kurala nasıl geldiği bilinmemektedir. Şimdiye kadar bulunan hemen hemen tüm çivi yazılı metinler, nasıl yapılacağına dair talimatlar olmaksızın, yalnızca tarifler şeklinde belirtilen çözümlerle ilgili problemler verir.

bulundular. Karşın yüksek seviye Babil'de cebirin gelişimi, çivi yazılı metinlerde negatif sayı kavramı ve ikinci dereceden denklemleri çözmek için genel yöntemler yoktur.

3. Avrupa'da ikinci dereceden denklemler XII – XVII yüzyıllar

Avrupa'daki el-Harezmi modeli üzerinde ikinci dereceden denklemleri çözme biçimleri ilk olarak 1202'de İtalyan matematikçi Leonardo Fibonacci tarafından yazılan "Abah Kitabı"nda tanımlanmıştır. Yazar bağımsız olarak bazı yeni cebirsel örnekler problem çözme ve Avrupa'da negatif sayıların tanıtımına yaklaşan ilk kişi oldu. Kitabı cebirsel bilginin sadece İtalya'da değil, Almanya, Fransa ve diğer Avrupa ülkelerinde de yayılmasına katkıda bulundu. "Abah Kitabı"ndaki birçok görev, neredeyse tüm Avrupa ders kitaplarına aktarıldı.XVI – XVII yüzyıllar ve kısmen XVIII içinde.

Tek bir kanonik forma indirgenmiş ikinci dereceden denklemleri çözmek için genel kuralX 2 + sevgili = ile tüm olası işaret ve katsayı kombinasyonlarıylab , c , Avrupa'da 1544 yılında M. Stiefel tarafından formüle edilmiştir. İkinci dereceden bir denklemi çözmek için formülün türetilmesi Genel görünüm Viet vardır, ancak Viet, aynı zamanda meslek olarak bir avukat olan ünlü Fransız bilim adamı Viet'in yalnızca olumlu köklerini tanıdı. İtalyan bilim adamları Tartaglia, Cardano, Bombelli ilkler arasındaXVIiçinde. Olumlu ve olumsuz köklere ek olarak dikkate alın. SadeceXVIIiçinde. Girrard, Descartes, Newton ve diğer bilim adamlarının çalışmaları sayesinde ikinci dereceden denklemleri çözme yöntemi modern bir görünüm kazanıyor.

III. İKİNCİ DENKLEMLERİ ÇÖZMENİN FARKLI YOLLARI

1. İkinci dereceden denklemin genel görünümü ve çözümü için standart formüller.

balta formunun denklemi 2 + in + c = 0 (1) , burada a, b, c - bazı sayılar vebir ≠ 0, kare denir.

İkinci dereceden bir denklem, ikinci dereceden bir denklem olarak da adlandırılır.

denklemde (1) a önce aradı katsayı, içinde- ikinci katsayı, İle birlikte - üçüncü katsayı veya ücretsiz üye.

Formun ifadesi D = içinde 2 – 4ac ikinci dereceden denklemin diskriminantı (ayırıcı) olarak adlandırılır.

Bilinmeyen bir denklemin kökünün (veya çözümünün)X yerine denklemde yerine koyarken sayı çağrılır.X doğru bir sayısal denklem elde edilir.

Bir denklemi çözmek, tüm köklerini bulmak veya hiç olmadığını göstermek anlamına gelir.

İkinci dereceden denklemin (1) köklerinin varlığı, diskriminantın işaretine bağlıdır.D, bu yüzden denklemin çözümü hesaplama ile başlamalıdır.Dikinci dereceden denklemin (1) kökleri olup olmadığını ve varsa kaç tane olduğunu bulmak için.

Üç durum mümkündür:

Eğer bir D>0, o zaman ikinci dereceden denklem (1) iki farklı gerçek köke sahiptir:

içinde 2 - 4ac.

Eğer bir D<0, то квадратное уравнение не имеет действительных корней.

Diyelim ki bir denklemde aşağıdaki dönüşümü yaptık: varsa parantezleri açtık, denklemin kesirli terimleri varsa paydaları yok ettik, tüm terimleri denklemin sol tarafına taşıdık ve benzer terimlerin indirgenmesini yaptık. Bundan sonra denklemin sol tarafında bilinmeyenin karesini içeren bir terim varsa ve bilinmeyeni daha yüksek derecede içeren bir terim yoksa, ikinci dereceden bir denklem elde edilir. Böyle bir denklemin genel biçimi, 2 + sevgili + c = 0.

katsayısına dikkat edina her zaman pozitif yapabiliriz, gerekirse, denklemin tüm terimlerinden önce işaretleri tersine çevirmek.

örnek 1

Oranları bulbir, içinde ve İle birlikte denklem için:
.

Çözüm:

Parantezleri genişletmek:
,

Paydayı yok etmek: 72 + 2x 2 = 15x 2 + 15x,

Tüm üyeleri sol tarafa aktarıyoruz ve alçıyı yapıyoruz: - 13x 2 - 15x + 72 = 0,

İşaretleri değiştir: 13x 2 + 15x - 72 = 0,

oranlar a, b , ve İle birlikte ikinci dereceden denklemin genel biçimi bu örnekte aşağıdaki özel değerleri almıştır:bir = 13, b = 15 ve c = - 72 .

Örnek 2

Denklemi çözün:

Çözüm: >0, iki kök;

Cevap: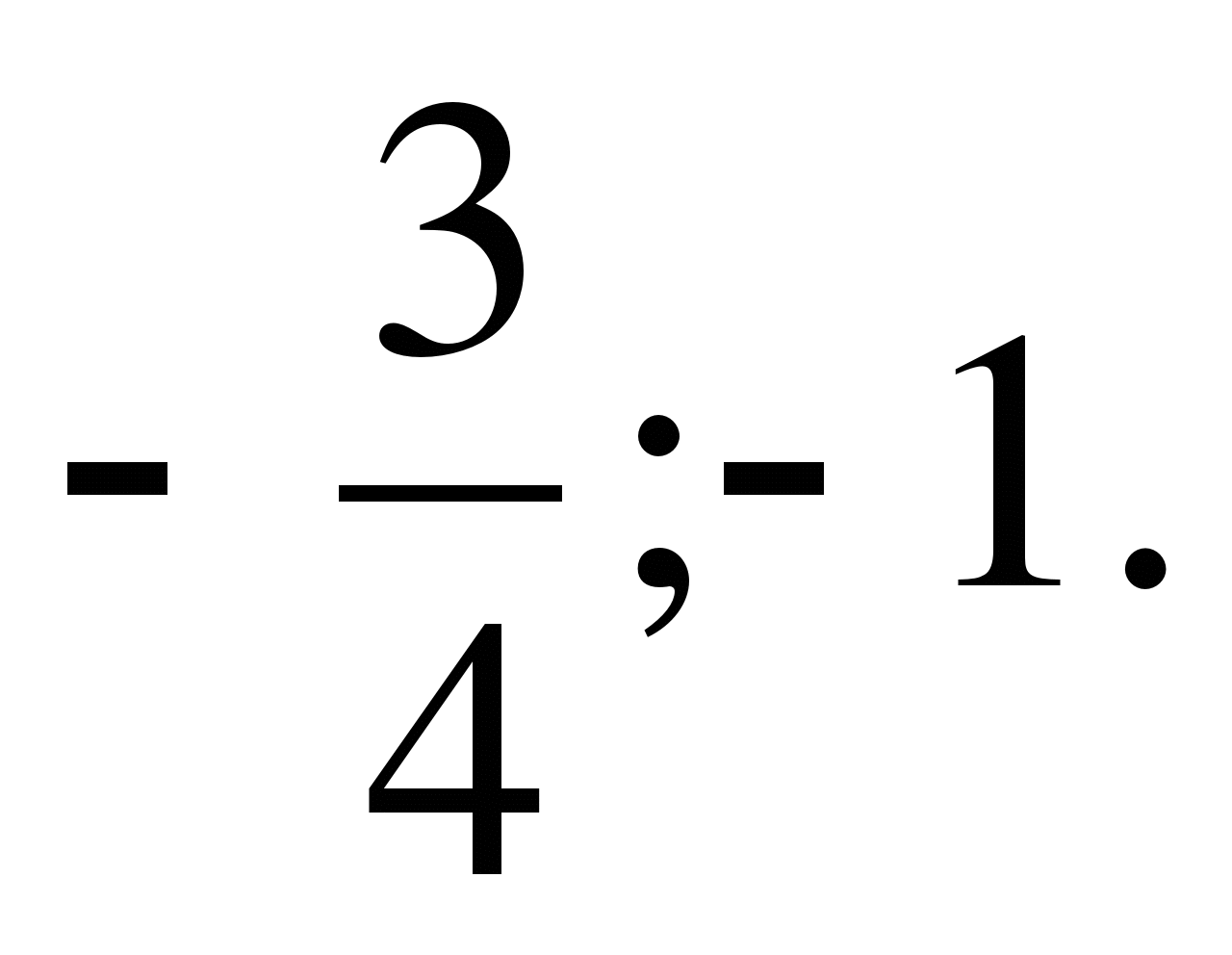

Örnek 3

Denklemi çözün:

Çözüm: D =0, bir kök;

Cevap:

Örnek 4

Denklemi çözün:

Çözüm:<0.

Denklemin reel kökü yoktur.

Cevap: Gerçek kökler yoktur.

İkinci dereceden denklemlerin çözümüne baktığımızda, bu denklemlerin bazen iki, bazen bir, bazen de kök olmadığını görüyoruz. Ancak, her durumda ikinci dereceden denklemlere atfetmeyi kabul ettiler.iki kök , köklerin bazen eşit, bazen de hayali olabileceğini söylemeye gerek yok. Böyle bir anlaşmanın nedeni, bir denklemin hayali köklerini ifade eden formüllerin gerçek köklere ait özelliklerin aynısına sahip olması, sadece hayali nicelikler üzerinde işlem yapmaktan ibaret olması, gerçek nicelikler için türetilen kuralların rehberliğinde olması ve bunun kabul edilmesidir. (
) 2 = - bir. Benzer şekilde, bir denklemin bir kökü olduğunda, bu kökü şu şekilde ele alabiliriz:iki özdeş, onlara denklemin farklı köklerine ait aynı özellikleri atfeder. Bu özelliklerin en basiti aşağıdaki teoremde ifade edilmektedir.

teorem: 2. derecede bilinmeyenin katsayısının 1 olduğu ikinci dereceden bir denklemin köklerinin toplamı, ters işaretle alınan birinci derecede bilinmeyenin katsayısına eşittir; bu denklemin köklerinin ürünü serbest terime eşittir.

Kanıt: Denklemin köklerinin α ve β ile gösterilmesiX 2 +px+ q = 0 , sahip olacağız (bu kökler ne ise)

Bu ürün, eşitlik temelinde kısaltılmış bir şekilde bulunabilir (a + b)(a – b) = a 2 – b 2 :

α ve β denklemin kökleri iseey 2 + sevgili + c = 0 veya aynı denklem nedir

, o zaman sahip olacak

.

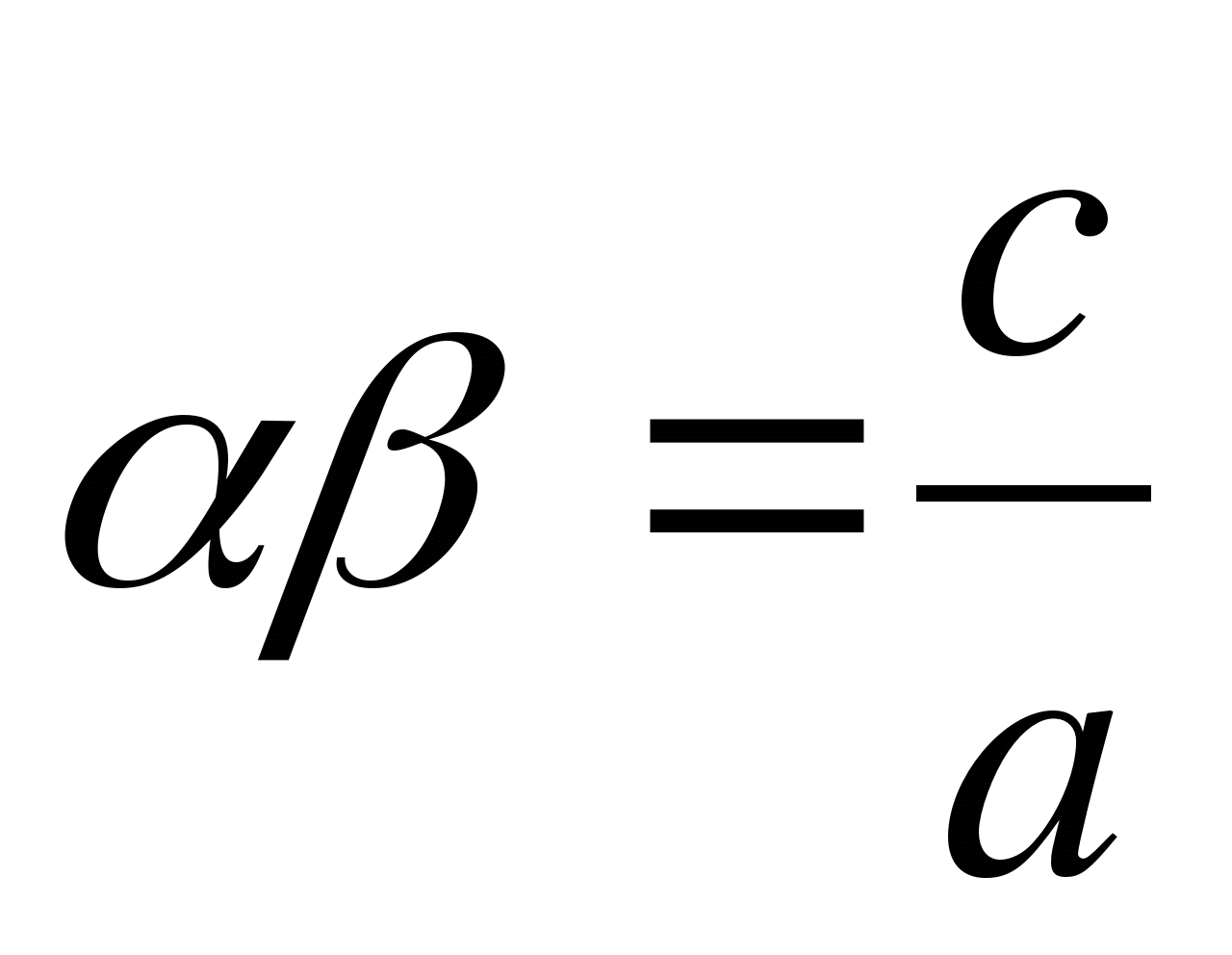Ters teoremi: miktarlar ise α, β, p ve q öyle mi α + β = - R ve αβ = q , sonra β ve α denklemin kökleriX 2 +px+ q = 0 .

Kanıt: miktarlarının her birinin kanıtlanması gerekmektedir.β ve α denklemi sağlarX 2 +px+ q = 0 . eşitlikten α + β = - p ve α \u003d -p - β , bundan sonra eşitlikαβ = q verir

veya
.

Anlamına geliyor, β denklemin köküey 2 + sevgili + c = 0 ; aynı şekilde, bunu doğrulayabilirizα aynı denklemin köküdür.

1. sonuç. Bu kökler ikinci dereceden bir denklem oluşturmak için kullanılabilir. Kökleri 2 ve - 3 olacak bir denklem oluşturmasına izin verin. 2 + (- 3) \u003d - p ve 2 (- 3) \u003d olduğunu varsayarsakq, buluyoruz - p \u003d 1, q= - 6. Dolayısıyla, istenen denklem şu şekilde olacaktır:

X 2 + x - 6 = 0

Benzer şekilde, - 2 ve - 2'nin x denkleminin kökleri olduğunu buluruz. 2 + 4x + 4 = 0, 3 ve 0, x denkleminin kökleridir 2 - 3x = 0, vb.

2. sonuç. İkinci dereceden bir denklemi çözmeden, eğer bu kökler gerçekse köklerinin işaretleri belirlenebilir. Örneğin, denklemimiz x olsun 2 + 8x +10 = 0. Bu örnekte sayı
- qpozitif bir sayı ise her iki kök de gerçek olmalıdır. Bu köklerin işaretlerini denklemleri çözmeden belirleyelim. Bunu yapmak için şu şekilde tartışıyoruz: İlk olarak serbest terime (+ 10) dikkat ederek + işareti olduğunu görüyoruz; yani köklerin ürünü olmalıpozitif , yani her iki kök deaynısı işaretler. Hangilerini belirlemek için, şu katsayıya dikkat edelim.X (yani +8'de) + işaretine sahiptir; bu nedenle, katsayıların toplamıolumsuz ; çünkü köklerde aynı işaretler olmalıeksi .

Benzer bir akıl yürütme, başka herhangi bir durumda köklerdeki işaretleri belirleyebilir. yani denklem x 2 + 8x - 10 = 0 farklı işaretli köklere sahiptir

(çünkü çarpımı negatiftir) ve negatif kök büyük bir mutlak değere sahiptir (çünkü toplamları negatiftir); denklem x 2 - 8 - 10 \u003d 0 ayrıca farklı işaretlere sahip köklere sahiptir, ancak büyük bir mutlak değer pozitif bir köke aittir.

2. Eksik ikinci dereceden denklemlerin çözümü.

İkinci dereceden bir denklem, içeren bir terim içermediğinde eksik olarak adlandırılır.X , veya serbest dönem yoktur. Eksik ikinci dereceden denklemler yalnızca aşağıdaki üç türden olabilir:

a) eksen 2 + c = 0; b) balta 2 + sevgili= 0; İle birlikte) balta 2 = 0.

Her bir çözüme bir göz atalım.

a) Denklemden X 2 + c = 0 bulur

ey 2 = - c ve x 2 = .

Bu eşitlik, bilinmeyenin karesinin sayıya eşit olmasını gerektirir. ; yani bilinmeyen, o miktarın kareköküne eşit olmalıdır. Bu ancak miktar pozitif bir sayıdır, ne zaman olurİle birlikte ve a zıt işaretlere sahip (örneğin,İle birlikte = - 8, a = + 2, öyleyse

işaretiyle gösterelim sadece karekökün aritmetik değerini ve pozitif bir sayının karekökünün iki değeri olduğunu dikkate alın; daha sonra, bir değeri ifade ederekX 1 , ve diğeri aracılığıyla X 2, yazabiliriz

eğer sayılar İle birlikte ve a aynı işarete sahip, o zaman negatif bir sayıdır; o zaman denklem ah 2 + c = 0 herhangi bir gerçek sayı ile sağlanamaz; bu durumda denklemin iki tane olduğu söylenir.hayali kök.

Örnek 5

Denklemi çözün:3x 2 – 27 = 0.

Çözüm: 3x 2 = 27; x 2 = 9; x =

Cevap: x =

Örnek 6

Denklemi çözün:X 2 +25 = 0.

Çözüm: x 2 = - 25; x =
; hayali kökler.

Cevap: x = + - 5 i.

b) denklemi çözmek içiney 2 + sevgili = 0 , şöyle hayal edelimX( balta + b ) = 0 . Çarpım, yalnızca faktörlerden herhangi biri olduğunda sıfıra eşit olabilir. sıfır; bu nedenle, eğer varsayarsak, söz konusu denklem tatmin edilir.x = 0 veya ah + b = 0 /

İkinci eşitlik verir
yani denklemey 2 + sevgili = 0 iki kökü vardır

x 1 = 0 ve

Örnek 7

Denklemi çözün: 2x 2 - 7x = 0.

Çözüm: 2x 2 – 7x = 0, x(2x – 7) = 0; X 1=0; x2 = .

Cevap: x 1 \u003d 0; x2 = .

içinde) Son olarak, ikinci dereceden denklembalta 2 = 0'ın açıkça tek bir çözümü vardır x = 0.

3. İkinci dereceden denklemlerin özel durumları.

a) Katsayının olduğu durumaçok küçük.

Denklem ekseninin köklerinin hesaplanması 2 + sevgili + c= 0 yukarıda türetilen genel formüle göre, bu durumda katsayı zor olduğundaa kıyasla çok küçük bir sayıb ve İle birlikte . Gerçekten de, kökleri formüle göre hesaplayarak

Çoğu durumda yaklaşık değerle yetinmeliyiz.
, ve dolayısıyla tüm pay. Bu yaklaşık değeri 2a'ya bölerek, böylece 2a'ya ve formülün payının hesaplandığı hatayı böleriz. Ancak, teklife göre, 2a çok küçük bir kesir olduğundan, küçük bir kesre bölmek, daha büyük bir sayı ile çarpmakla eşdeğer olduğundan, hata önemli ölçüde artar, bunun sonucunda nihai sonuç gerçek olandan uzak olacaktır. Örneğin, 2a = 0.0001 ise ve hesapladığımızda
dördüncü ondalık basamağa kadar, nihai sonuçtaki hata payı 0,0001: 0,00001 = 10 olacaktır.

Bu durumda denklemin köklerini hesaplamak için, sözde daha uygun bir yöntemardışık yaklaşım.

Çok küçük bir değer için unutmayına denklemin köklerinden biri biraz farklıdır , ve diğeri çok büyük bir sayıdır (mutlak değerde). Gerçekten de, denklem 2 + sevgili + c= 0 denkleme eşdeğerdir

hangi görünüm verilebilir

Çünkü - a sıfıra yakınsa, son denklem bu tür değerlerle karşılanabilirX , denklemin sol tarafındaki faktörlerden birinin çok küçük bir sayı olduğu ve diğerinin çok büyük olmadığı; bu gerçekleşecek ya da biz verdiğimizdeX çok büyük bir mutlak değer veyaX yakın olacak .

Köklerden biraz farklı olan köklerden birinin nasıl hesaplanacağını gösterelim.

(birincisini çıkararak başka bir kök buluruz ).

Çıkardığımız denklemden
.

Çünkü a çok az sayıda veX ve b çok büyük ve çok küçük değil, o zaman kesrin mutlak değeri
çok küçük. Bu terimi ihmal edersek,x ilk yaklaşım

Bu değeri denklem (1)'in sağ tarafına ekleyerek,ikinci yaklaşım, ilkinden daha doğru:

Bu miktarı denklem (1)'in ilk kısmına ekleyerek, elde ederiz.üçüncü yaklaşım , daha da doğru. Benzer şekilde, gerekirse dördüncü ve sonraki yaklaşımı elde edebiliriz.

Örnek 8

Denklemi çözün: 0.003x 2 + 5x - 2 = 0

Çözüm:
.

İlk yaklaşım = 0.4. Bu sayı x'in daha gerçek değeridir 2 çünkü atmak zorunda kaldıkolumsuz üye - 0.0006x 2.

İkinci yaklaşım = 0,4 - 0,0006 (0,4) 2 = 0.399904. Bu sayı gerçek değerden küçükX 2 x'ten büyük sayı 2 , bu da çıkanın artmasına ve farkın azalmasına neden olur.

Üçüncü yaklaşım gerçek değerden daha büyük olacaktır.X , dördüncü daha az, vb.

0.4 > x > 0.399904 olduğundan, almak yerineX bu yaklaşımlardan biri için 0,4 - 0,399904'ten küçük, yani 0,0001'den küçük bir hata yapacağız. Bulunan kökten çıkarılarak başka bir kök elde edilir.
İlk kök için 0,4 sayısını alırsak diğeri 1667, (6) olur.

b) Durum ne zaman İle birlikte çok küçük bir sayı.

Ardışık yaklaşım yöntemi, denklemin serbest terimi, denkleme kıyasla çok küçük bir sayı olduğunda da uygulanabilir.a ve b . Bu durumda, köklerden biri yakın
diğeri ise çok küçük bir miktar. Denklemin form verilip verilmediğini doğrulamak kolaydır.

Teklife göre mutlak değer,İle birlikte çok küçükse, o zaman denklem açıkça tatmin edilecektir.X veya 0'a çok yakın veya çok az farklı

Çok küçük bir değere sahip bir kök bulmak için denklemi tekrar formda temsil ediyoruz.

Çünkü a ve b sayıların özü çok büyük ve çok küçük değil mutlak değerdirX 2 çok küçüktür, o zaman ilk tahmin için terimi ihmal edebiliriz.
; o zaman alırız
.

Bu değeri yerine yerleştirmeX (1) denkleminin sağ tarafında, ikinci yaklaşımı elde ederiz; benzer şekilde, gerekirse aşağıdaki yaklaşımları buluruz.

4. Vieta teoremini kullanarak denklemleri çözme

(doğrudan ve ters).

Verilen ikinci dereceden denklem forma sahiptir

Kökleri Vieta teoremini tatmin eder;a =1 formu var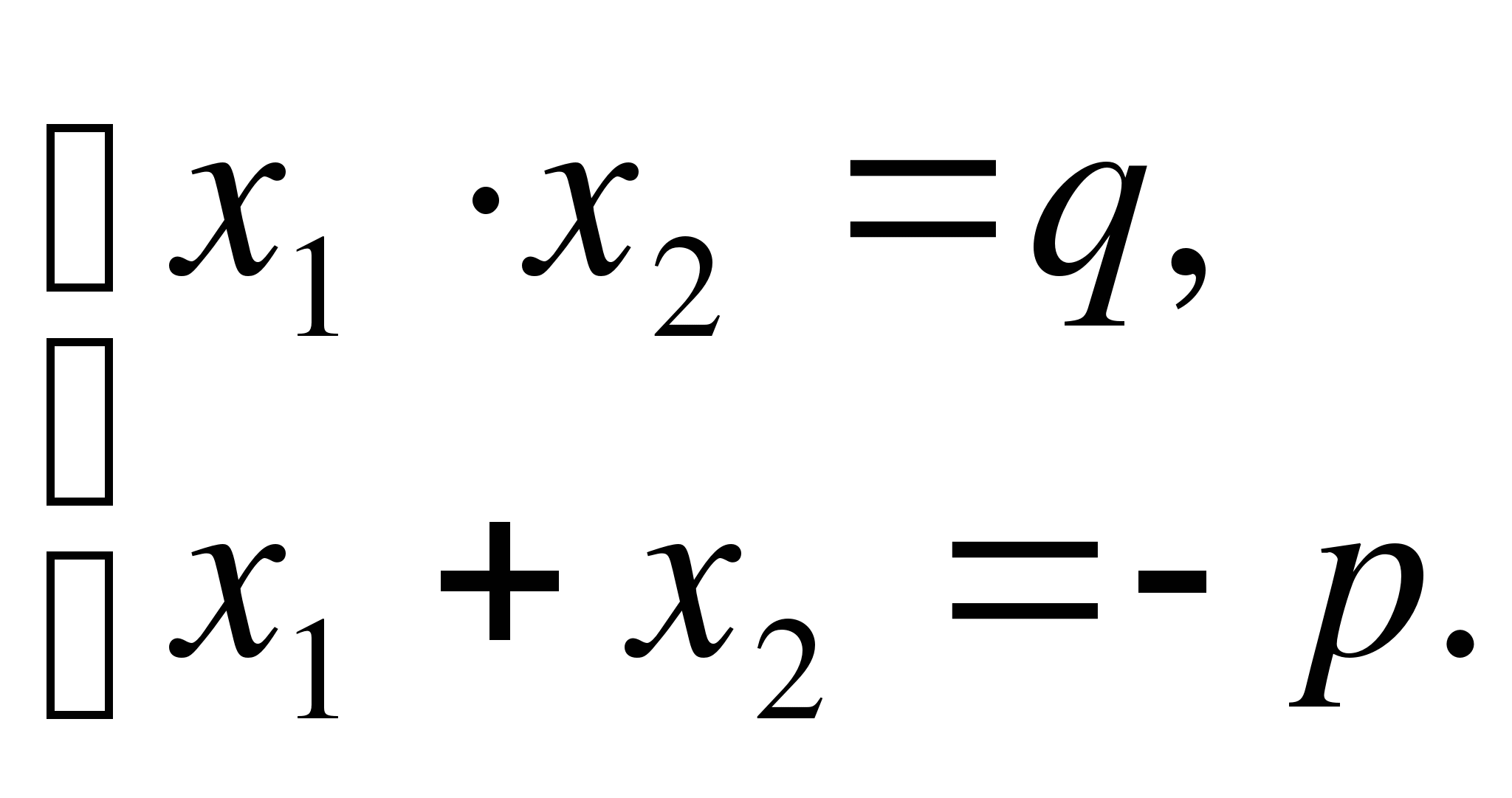

a) Ücretsiz üye iseq verilen ikinci dereceden denklemin pozitif olması durumunda denklemin iki kökü vardır ve bu ikinci katsayıya bağlıdırp . Eğer bir p >0 , o zaman her iki kök de negatifsep <0 , o zaman her iki kök de pozitiftir.

Örnek 9

Örnek 10

b) Ücretsiz üye iseq Yukarıdaki denklemin negatif olması durumunda denklemin farklı işaretli iki kökü vardır ve eğer mutlak değerdeki daha büyük kök pozitif olurp <0, veya olumsuz isep >0 .

Örnek 11.

Örnek 12.

Örnek 13

Denklemin köklerini bulun: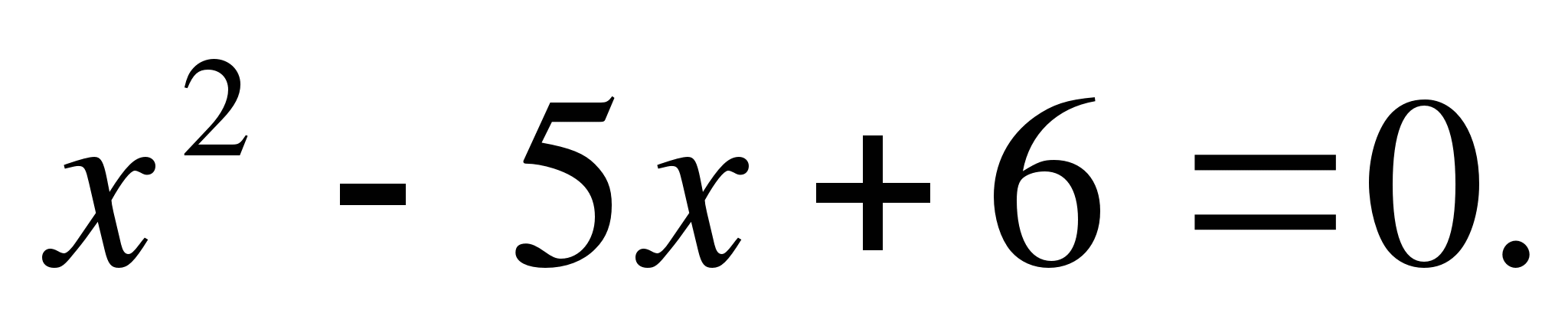

Çözüm: burada p=-5, q=6. iki sayı seç x 1 ve x 2 yani

Vieta teoremine göre

Cevap:

5. İkinci dereceden bir denklemin katsayılarının özellikleri.

a) İkinci dereceden denklem verilsin

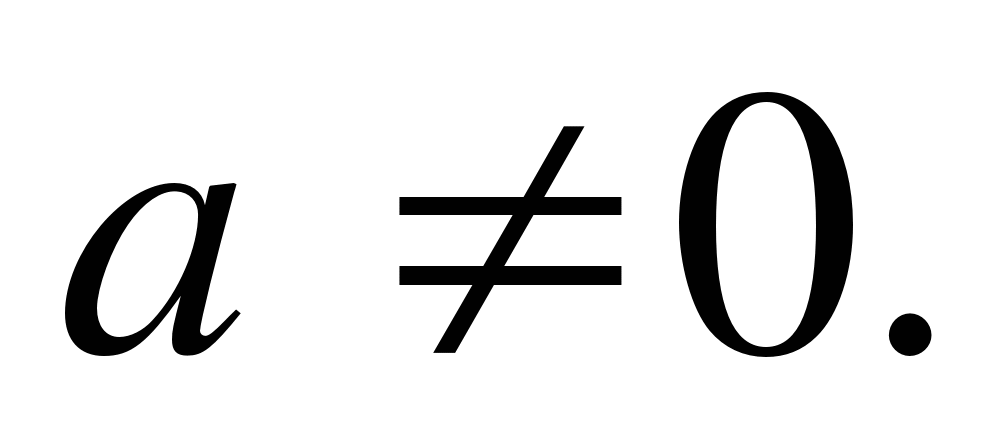
1. Eğer bir a + b + c \u003d 0 (yani, denklemin katsayılarının toplamı sıfırdır), sonra

Kanıt: Denklemin her iki tarafını dabir ≠ 0 , indirgenmiş ikinci dereceden denklemi elde ederiz

Vieta teoremine göre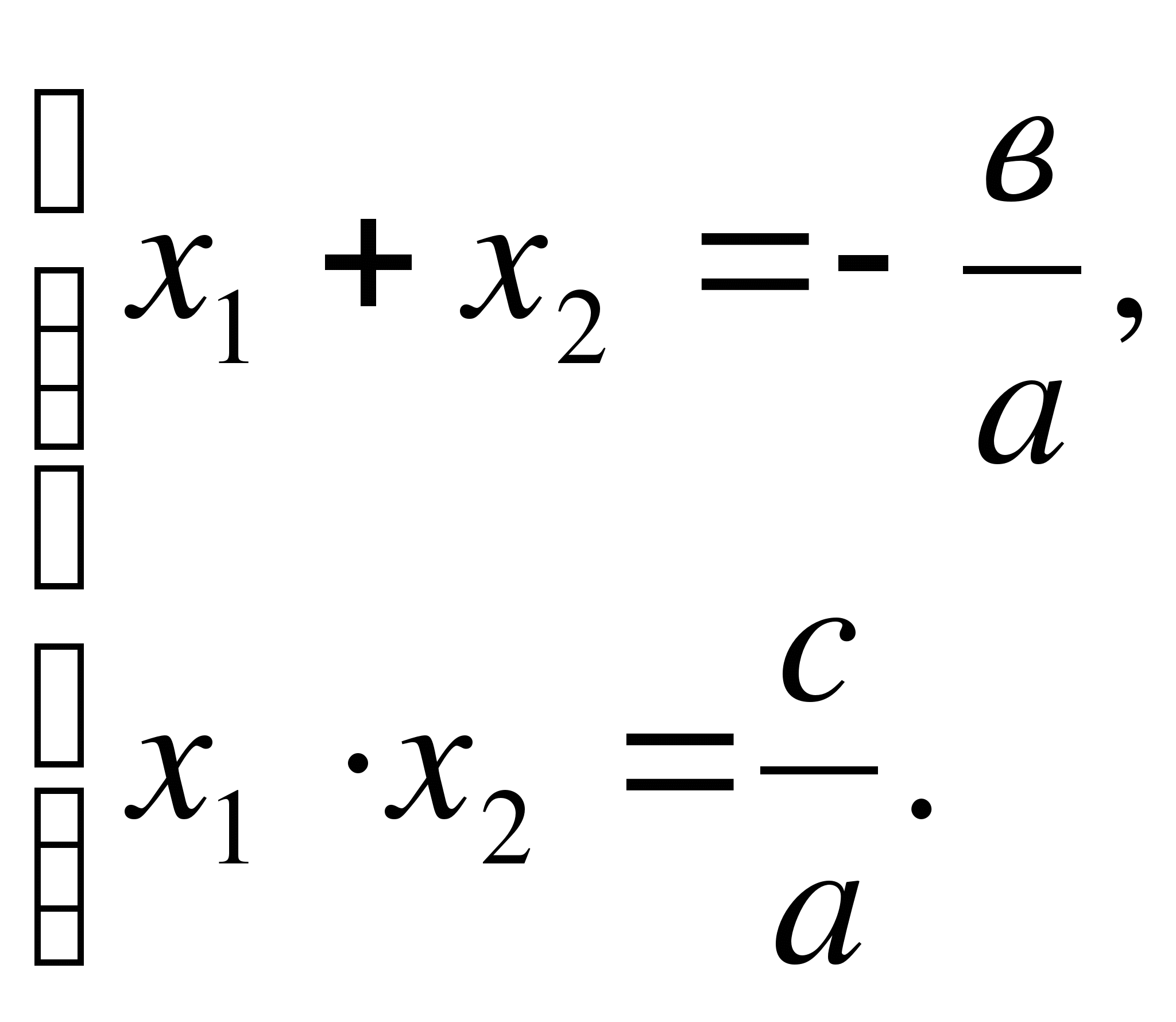

koşula göre a + b + c = 0, nerede c = - a - s. Anlamına geliyor,

alırız
Q.E.D.

2. Eğer bir a - b + c \u003d 0 veya b \u003d a + c, sonra

Kanıt: Vieta teoremine göre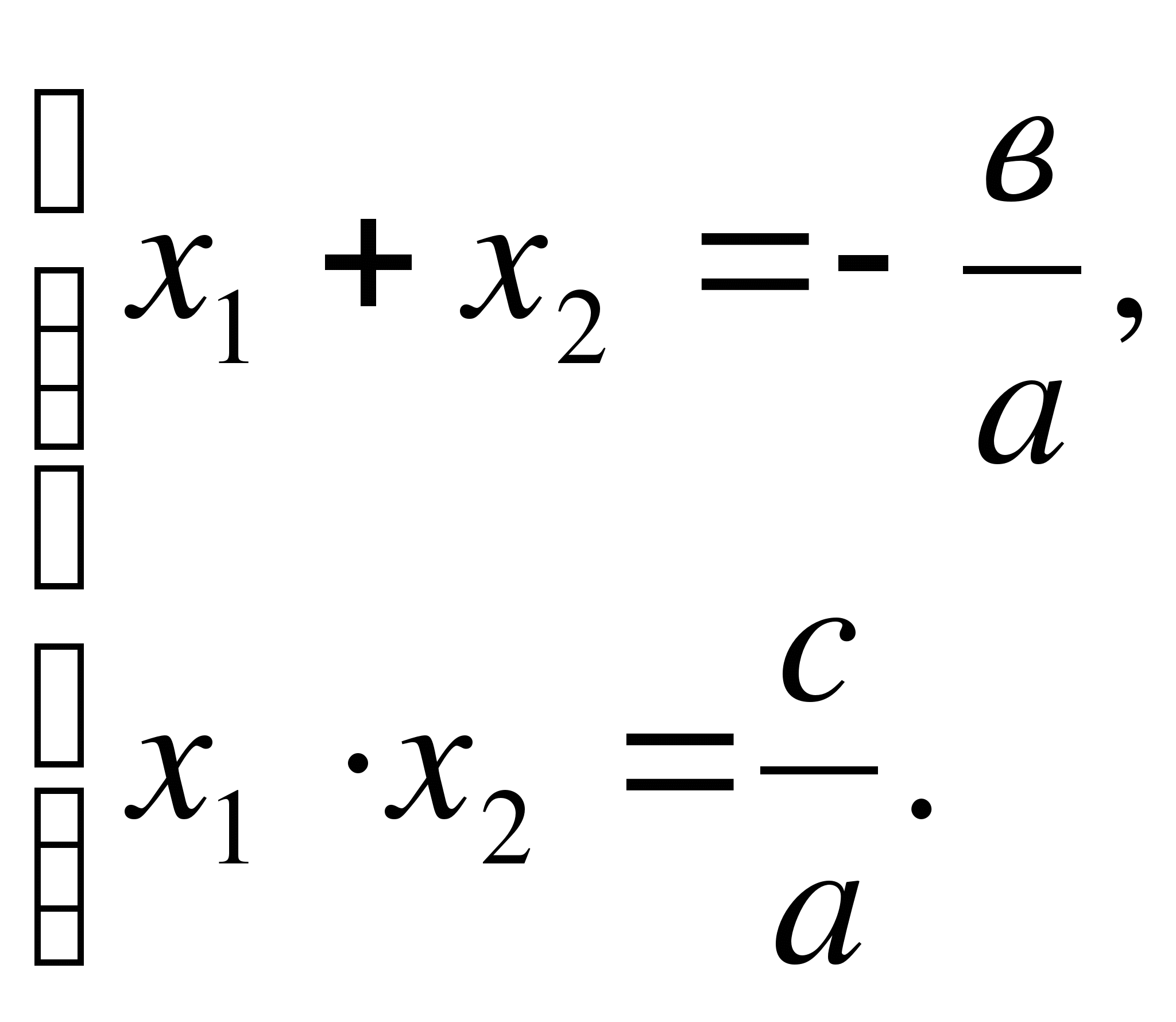

koşula göre a - c + c = 0, nerede c = bir + c. Böylece,

şunlar.
Q.E.D.

3. denklemde ise

Kanıt: Gerçekten de, bu denklemi indirgenmiş formda sunuyoruz.

Denklemi formda yazıyoruz

Bu formda yazılan denklem, kökleri hemen almanızı sağlar.

4. Eğer bir a = - c = m · n , = m 2 – n 2 , o zaman köklerin farklı işaretleri vardır, yani:

Kesirlerin önündeki işaretler ikinci katsayının işareti ile belirlenir.

6. "Transfer" yöntemini kullanarak denklemleri çözme.

İkinci dereceden denklemi düşünün

ey 2 + b x + c= 0 ve ≠ 0.

Her iki tarafı da çarparaka, denklemi elde ederiz

a 2 X 2 + bir b x + ac = 0.

İzin vermek ey= y, nereden X = ; sonra denkleme geliyoruz

de 2 + ile + ac = 0,

buna eşdeğer.

kökleri de 1 ve de 2 Vieta teoremi yardımıyla bulun. Sonunda x'i elde ederiz 1 = onlara 1 = . Bu yöntemle katsayıa serbest terimle çarpılır, sanki ona "atılmış" gibi, bu yüzden deniraktarım yöntemi. Bu yöntem, Vieta teoremini kullanarak bir denklemin köklerini bulmak kolay olduğunda ve en önemlisi, diskriminant tam bir kare olduğunda kullanılır.

Örnek 14

Denklemi çözün: 2x 2 - 11x + 15 = 0.

Çözüm: 2 katsayısını serbest terime "aktaralım", sonuç olarak denklemi elde ederiz:

de 2 – 11 y + 30 = 0.

Vieta teoremine göre

Cevap: 2,5; 3.

7. Grafik çözüm ikinci dereceden denklem.

denklemde ise
ikinci ve üçüncü terimleri sağa kaydırırsak

Bağımlılık grafikleri oluşturalım
ve

İlk bağımlılığın grafiği, orijinden geçen bir paraboldür. İkinci bağımlılığın grafiği düz bir çizgidir (Şekil 1).

Aşağıdaki durumlar mümkündür:

Düz bir çizgi ve bir parabol iki noktada kesişebilir, kesişme noktalarının apsisleri ikinci dereceden bir denklemin kökleridir;

Doğru ve parabol birbirine değebilir (sadece bir ortak nokta), yani. denklemin bir çözümü vardır;

Düz çizgi ve parabolün ortak noktaları yoktur, yani. ikinci dereceden denklemin gerçek kökü yoktur. Örnek 15

Denklemi çözün:2 x 2 + 6 x – 5 = 0.

Çözüm: Denklemi ikiye bölün:y = 2 x 2 ve y = 6 x – 5.

Yardımcı bir tablo oluşturalım:

y = 2 x 2 -5

y = 6 x – 5

Fonksiyonların grafiklerini oluşturalımy = 2 x 2 ve y = 6 x – 5.

İki denklemin iki noktada kesiştiği grafikten görülebilir.X 1 onlara 2 yani denklemin iki kökü olacakX 1 ≈ - 1.1 ve x 2 ≈ 2,7.

Cevap: x 1 ≈ - 1.1 ve x 2 ≈ 2.7.

8. İkinci dereceden denklemleri pergel ve cetvelle çözme.

Bir parabol kullanarak ikinci dereceden denklemleri çözmenin grafik yolu elverişsizdir.

Nokta nokta bir parabol oluşturursanız, çok zaman alır ve elde edilen sonuçların doğruluk derecesi düşüktür.

İkinci dereceden bir denklemin köklerini bulmak için aşağıdaki yöntemi öneriyoruz.

pusula ve cetvel kullanarak (Şek. 5).

İstenen dairenin ekseni kestiğini varsayalım.

B noktalarındaki apsis(X 1 ;0) ve D(X 2 ;0), nerede X 1 ve X 2 denklemin kökleri
ve A(0;1) ve C noktalarından geçer
y ekseninde. Daha sonra teoreme göreÖOB O sahip olduğumuz sekanslarD= ОА OS, nereden OS =

Dairenin merkezi, diklerin kesişme noktasındadır.bilimkurgu ve SK, AC ve B akorlarının orta noktalarında restore edildiD,bu yüzden

Yani:

1) puan oluşturmakS
(daire merkezi) ve A(0;1);

2) yarıçaplı bir daire çizinSA;

3) bu dairenin O ekseni ile kesişme noktalarının apsisiX orijinal ikinci dereceden denklemin kökleridir.

Bu durumda, üç durum mümkündür.

1. Dairenin yarıçapı, merkezin ordinatından büyük
daire O eksenini kesiyorX iki noktada (Şekil 6a) B(X 1 ;0) ve D(X 2 ;0), nerede X 1 ve X 2
1) Çemberin yarıçapı, merkezin koordinatından büyük
daire O eksenini kesiyorX iki noktada (Şekil 6a) B(X 1 ;0) ve D(X 2 ;0), nerede X 1 ve X 2 ikinci dereceden denklemin kökleridir

2. Dairenin yarıçapı, merkezin koordinatına eşittir
daire O eksenine dokunuyorX (Şek. 6,b) B noktasında(X 1 ;0), nerede X 1 ikinci dereceden denklemin köküdür.

3. Dairenin yarıçapı, merkezin ordinatından küçük
dairenin apsis ekseni ile ortak noktası yoktur (Şek. 6,içinde ), bu durumda denklemin çözümü yoktur.

a)
iki kökX 1 ve X 2 .

b)
bir kökX 1 .

içinde)
Gerçek kökler yoktur.

Örnek 16

Denklemi çözün:

Çözüm: bkz. şek.7.

Dairenin merkezinin koordinatlarını formüllerle belirleyin:

Bir yarıçap çemberi çizelimSA, burada A (0; 1), S(1; -1).

Cevap 1; 3.

Örnek 17.

Denklemi çözün:
S bkz. Bradis V.M (tümü cm cinsinden), üçgenlerin benzerliğinden

Örnek 20.

denklem için

z 2 – 9 z + 8 = 0.

Nomogram kök verir

z 1 = 8, 0 ve z 2 = 1, 0 (Şek. 12).

Bir nomogram ile çözün

nomogram denklemi

2 z 2 – 9 z + 2 = 0.

Bunun katsayılarını böl

2 ile denklemler, denklemi elde ederiz

z 2 – 4, 5 + 1 = 0.

Nomogram kök verirz 1 = 4 vez 2 = 0,5.

Örnek 21.

denklem için

z 2 + 5 z – 6 = 0

nomogram verir pozitif

kökz 1 = 1.0 ve negatif

çıkararak kökü bul

pozitif kök

itibaren– R, şunlar. z 2 = – R - 1 =

= – 5 – 1 = – 6.0 (Şekil 13.)

10. İkinci dereceden denklemleri çözmek için geometrik yöntem.

Geometrinin cebirden daha gelişmiş olduğu eski zamanlarda, ikinci dereceden denklemler cebirsel olarak değil geometrik olarak çözülürdü. Harezmi'nin cebirden meşhur olmuş bir örneği verelim.

Örnek 22.

x denklemini çöz 2 + 10x = 39.

Orijinalde bu problem şu şekilde formüle edilmiştir: "Kare ve on kök 39'a eşittir."

Çözüm: Kenarı x olan bir kare düşünün, kenarlarına her birinin diğer kenarı 2, 2 olacak şekilde dikdörtgenler inşa edilmiştir. = – 8.

de 2

3 yıl

Örnek 24.

Denklemleri geometrik olarak çözün 2 – 6y – 16 = 0.

Denklemi dönüştürürsek,

de 2 - 6y \u003d 16.

Şek. y ifadesinin "görüntülerini" bulun 2 - 6y, yani bir kenarı olan bir karenin alanındande Kenarı 3'e eşit olan karenin alanını iki kez çıkarın.

Öyleyse, eğer y ifadesi 2 - 6y 9 ekleyin, sonra y - 3 kenarı olan bir karenin alanını elde ederiz. y ifadesinin yerine 2 - 6y eşittir, şunu elde ederiz: (y - 3) 2 = 16 +9, yani y – 3 = ±
veya y - 3 = ± 5, burada y 1 = 8 ve y 2 = – 2.

y - 3

IV. ÇÖZÜM

Bu çalışmanın sonucunda aşağıdaki sonuçlar çıkarılabilir:

Yapılan çalışmanın konusuyla ilgili bilimsel ve metodolojik literatürün incelenmesi, ikinci dereceden denklemleri çözmek için çeşitli yöntemlerin kullanılmasının matematik çalışmasında önemli bir bağlantı olduğunu, ilgiyi artırdığını, dikkat ve yaratıcılığı geliştirdiğini göstermiştir.

Dersin farklı aşamalarında çeşitli denklem çözme yöntemlerini kullanma sistemi, öğrencileri harekete geçirmenin etkili bir yoludur, bilgi, beceri kalitesini arttırmada olumlu bir etkiye sahiptir ve zihinsel aktiviteyi geliştirir.

İkinci dereceden denklemleri çözmedeki ana şey, doğru rasyonel çözme yolunu seçmek ve çözüm algoritmasını uygulamaktır.

Bu konu üzerinde çalışmak, farklı denklemleri çözmenin çeşitli yollarının daha fazla araştırılmasına katkıda bulunur.

v.EDEBİYAT

Büyük Sovyet Ansiklopedisi.– M., Sovyet Ansiklopedisi, 1974.

Gazete "Matematik".– "Bir Eylül" yayınevi.

Glazer G.I. Okulda matematik tarihi. 7-8 sınıf.– M., Eğitim, 1982.

Çocuk ansiklopedisi. 2.– M., Pedagoji,1972.

Dorofeeva VA. Matematik derslerinde tarih sayfaları.– Lvov, Quantor,1991.

Liman M.M. Okul çocukları matematik ve matematikçiler hakkında.– M., Aydınlanma,1981.

Çocuklar için ansiklopedi.– M., Avanta+, 1997.

Alimov Ş.A., İlyin V.A. ve diğerleri Cebir, 6-8. 6-8. sınıflar için deneme kitabı lise. – M., Aydınlanma,1981. ;

bradis VM dört haneli matematik tabloları lise için. Ed. 57.– M., Aydınlanma,1990. 83.

Zlotsky G.V. Matematik öğretiminde görev kartları. Öğretmen için kitap.– M., Eğitim, 1992.

Klyukvin M.F. Cebir, 6-8. öğrenci yardımı6-8 sınıflar.– M., Eğitim, 1963.

Kuzhepov A.K., Rubanov A.T. cebir ve temel fonksiyonlar. öğretici ikincil özel için Eğitim Kurumları. – M., lise1969.

Matematik ("Pervoe Eylül" gazetesinin eki), No. 21/96, 10/97, 24/97, 18/98, 21/98.

Okunev A.K.. ikinci dereceden fonksiyonlar, denklemler ve eşitsizlikler. Öğretmen için bir rehber.– M., Eğitim, 1972.

Presman AA.Pusula ve cetvelle ikinci dereceden bir denklemi çözme.– M., Kvant, No. 4/72. 34.

solomnikB. C., Miloye P.I. Matematikte soru ve görevlerin toplanması. Ed. 4, ekleyin.– M., Yüksek Lisans, 1973.

Khudobin A.I.. Cebir ve temel fonksiyonlarda problemlerin toplanması. Öğretmen için bir rehber. Ed. 2.– M., Eğitim, 1970.

Aydınlatılmış.Pentkovsky M.V., Çizimleri sayma. (Nomogramlar), 2. baskı, M., 1959;

proje
yaratıcı proje adı
Slogan: Matematikte küçük numaralar büyük rol oynar.
Proje yazarı: Rylova Victoria
1 numaralı 8G sınıfı MOU ortaokulu öğrencisi
derinlemesine çalışma ile
bireysel öğeler "Poliforum"

Projenin ana sorusu:
Çözümler ne kadar çeşitli
ikinci dereceden denklemler?
Hipotez:
Sanırım ikinci dereceden denklemler çözülebilir
birkaç farklı şekilde
Hedef:
Teorik temellerin incelenmesi ve uygulanması
kare çözmenin farklı yollarını uygulayın
denklemler

Görevler:
1. Konuyla ilgili bilgileri yazılı olarak alın
kaynaklar ve internet
2. Plana göre bilgileri sentezleyin
3. Kareyi çözmenin farklı yollarını keşfedin
denklemler ve materyali pratikte test edin
Çalışma planı:
Projenin konusunun ve amacının tanımı,
araştırma konusunun formülasyonu
Bilgi kaynağının belirlenmesi
Nasıl toplanacağını ve analiz edileceğini belirleme
bilgi
Sunum Yönteminin Belirlenmesi
Sonuçlar

dipnot

Proje "Kare çözme yöntemleri
denklemler" çalışmanın sonuçlarını yansıtır,
ne var hakkında benim tarafımdan yürütülen
ikinci dereceden denklemleri çözmenin yolları ve ne
bu kendin ve benim için faydalı olabilir
Arkadaş.
Projenin teması, kullanımla ilgilidir.
ikinci dereceden denklemleri çözmenin yolları
bilinen hakkında bilinmeyeni bulmak.
Matematik okulda öğretilir
ile ikinci dereceden denklemlerin kökleri için formüller
herhangi birini çözmek için kullanılabilir
ikinci dereceden denklemler.
Ancak başka çözümler de var
çok hızlı bir şekilde yapmanızı sağlayan denklemler ve
ikinci dereceden denklemleri rasyonel olarak çözer.

Meydanın tarihinden
denklemler
İkinci dereceden denklemler yaklaşık 2000 yıldır çözülmüştür
M.Ö e. Babilliler. modern uygulama
cebirsel gösterim, onların içinde söyleyebiliriz
eksik olanlar hariç çivi yazılı metinler bulunur ve
tam ikinci dereceden denklemler gibi:
Şimdiye kadar bulunan neredeyse tüm çivi yazısı yazıları
metinler sadece çözümleri olan problemler verir,
talimat olmadan reçete şeklinde belirtilen
nasıl oldukları hakkında
bulundu.

Hintli bilgin Brahmagupta (7. yüzyıl),
genel kuralı özetledi
ikinci dereceden denklemler
tek kanonik form:
ax2 + bx = c, a > 0
Denklemde, a hariç katsayılar,
olumsuz olabilir. kural
Brahmagupta temelde aynıdır
bizim.
Brahmagupta
İkinci dereceden denklemleri çözmek için formüller
İlk olarak bir kitapta yayınlandı
İtalyan bir matematikçi tarafından yazılmış
Leonardo Fibonacci (XIII yüzyıl). x2 + bx = c,
tüm olası işaret kombinasyonları ile
katsayılar b, c idi
Avrupa'da sadece 1544'te formüle edilmiştir.
Leonardo Fibonacci

Sadece XVII yüzyılda. Girard, Descartes, Newton ve
diğer bilim adamlarının ikinci dereceden denklemleri çözme yolu
modern bir görünüm kazanıyor.
Bence
Sonuç olarak,
mevcut.
Descartes
bir dahi var
düşünce sabır,
odaklanmış
ünlü
yön.
Newton
Tüm Denklemler
cebir var
çok fazla karar
kaç
gösteriler
İsim
en yüksek
miktarları.
girard
tüm matematikçiler
altında olduğunu biliyordu
cebir gizlendi
eşsiz
hazine, ama
onları bulabildiler
viet

Geometrik
çözüm yolu
Meydan
denklemler
Çözüm
Meydan
denklemler
kullanarak
nomogramlar
Çözüm
Meydan
denklemler
bir daire kullanmak
ve hükümdarlar
Çözümler
Meydan
denklemler
yol
"transferler"
Ayrışma
ayrıldı
denklemin parçaları
çarpanlar
Çeşitli
yollar
çözümler
Meydan
denklemler
grafik
çözüm
Meydan
denklemler
Yöntem
tahsis
tam kare
Yöntem
katsayılar
Çözüm
Meydan
denklemler
formüle göre
Çözüm
denklemler
kullanarak
Vieta'nın teoremleri

1. YÖNTEM: Denklemin sol tarafını çarpanlara ayırma

Hedef:
ikinci dereceden bir denklem ver
genel görünüm
A(x) B(x)=0,
burada A(x) ve B(x) -
x'e göre polinomlar.
yollar:
için ortak faktörü çıkarmak
parantez;
formülleri kullanma
kısaltılmış çarpma;
gruplandırma yöntemi.
denklemi çözelim
x2 + 10x - 24 = 0.
Sol tarafı çarpanlarına ayıralım:
x2 + 10x - 24 =
\u003d (x + 12) (x - 2).
Sonuç olarak,
(x + 12)(x - 2) = 0
Ürün sıfır olduğu için
faktörlerinden biri sıfıra eşittir. Bu nedenle sol taraf
Denklem x = 2'de ve ayrıca x = - 12'de kaybolur.
Bu, 2 ve - 12 sayısının kök olduğu anlamına gelir.
denklemler x2 + 10x - 24 = 0.

2. YÖNTEM: Tam kare seçim yöntemi.

Yöntemin özü: genel bir ikinci dereceden denklem getirmek
tamamlanmamış ikinci dereceden denklem.
x2 + 6x - 7 = 0 denklemini çözelim.
Sol tarafta tam bir kare seçelim.
Şimdi denklemin sol tarafını dönüştürüyoruz
x2 + 6x - 7 = 0, toplama ve 9 çıkarma.
Sahibiz:
x2 + 6x - 7 =
\u003d x2 + 2 x 3 + 9 - 9 - 7 \u003d
\u003d (x + 3) 2 - 9 - 7 \u003d (x + 3) 2 - 16.
Böylece, bu denklem yazılabilir
Yani:
(x + 3) 2 - 16 \u003d 0,
(x + 3)2 = 16.
Bu nedenle, x + 3 - 4 = 0 veya x + 3 = -4
x1 = 1,
x2 = -7.

3. YÖNTEM: Kareyi çözme
formüle göre denklemler
1
b 0, c 0
D>0
2 kök
D=0
1 kök
x piksel g 0
2
D<0 Нет корней
Kök formülleri:
2
1
x1.2
p
2
bb 2 4ac
x1, 2
;
2a
2
p
g;
4
3
x1, 2
k k 2 ac
a

4. YÖNTEM: Vieta teoremini kullanarak denklemleri çözme.

Bilindiği gibi, verilen ikinci dereceden denklem forma sahiptir
x2 + piksel + c = 0. (1)
Kökleri, a = 1 için forma sahip olan Vieta teoremini karşılar.
x1 x2 = q,
Bundan şu sonuçları çıkarabiliriz
x1 + x2 = -p
(p ve q katsayılarından işaretler tahmin edilebilir
kökler).
(q > 0 ise) denklemin iki özdeş
kökün işareti ve bu, ikinci katsayı p'nin kıskançlığıdır.
Mümkünse< 0, то оба корня отрицательны.
Mümkünse< 0, то оба корня положительны.

5. YÖNTEM: "Transfer" yöntemini kullanarak denklemleri çözme.

Bu yöntemle a katsayısı serbest terim ile çarpılır.
ona "atılır", bu yüzden buna "aktarma" yöntemi denir.
Bu yöntem, denklemin köklerini bulmanın kolay olduğu durumlarda kullanılır.
Vieta teoremini kullanarak ve en önemlisi, diskriminant olduğunda
mükemmel kare
2x2 - 11x + 15 = 0 denklemini çözelim.
2 katsayısını serbest terime "atalım",
sonuç olarak denklemi elde ederiz
y2 - 11y + 30 = 0.
Vieta teoremine göre y \u003d 5, y \u003d 6, sonra x1 \u003d 5/2, x \u003d 6/2
Cevap: 2.5; 3.

6. YÖNTEM: İkinci dereceden bir denklemin katsayılarının özellikleri

ikinci dereceden denklem olsun
ax2 + bx + c = 0, burada a ≠ 0.
a + b + c \u003d 0 ise, o zaman
x1 1, x2
c
a
b = a + c ise, o zaman
x1 1, x2
c
a
1978x1984x60
2
x1 1;
6
x2
1978
319 x 2 1988 x 1669 0
x1 1;
1669
x2
.
319

7. YÖNTEM: İkinci dereceden bir denklemin grafik çözümü

denklemi dönüştürmek
x2 + piksel + q = 0
x2 = - piksel - q.
y \u003d x2 ve y \u003d - px - q bağımlılık grafikleri oluşturalım.
İlk bağımlılığın grafiği geçen bir paraboldür.
kökeni aracılığıyla. Program iki
bağımlılıklar - düz çizgi (Şekil 1). Aşağıdakiler mümkündür
vakalar:
Doğrudan ve
parabol olabilir
dokunma (yalnızca
ortak bir
nokta), yani
denklem var
bir çözüm;
düz ve
parabol değil
ortak noktaları var
şunlar. Meydan
denklem değil
kökler.
düz çizgi ve parabol
kesişebilir
iki nokta, apsis
puan
kavşaklar
vardır
kökler
Meydan
denklemler;

8. YÖNTEM: İkinci dereceden denklemleri pusula ve cetvelle çözme.

ax2 + bx + c = 0
Yani:
1) inşa noktaları (daire merkezi)
ve A(0; 1);
2) yarıçaplı bir daire çizin
SA;
3) bunun kesişme noktalarının apsisleri
x ekseni olan daireler
orijinal karenin kökleri
denklemler.
2) daire x eksenine değiyor
Bu durumda, üç durum mümkündür.
1) daire ekseni kesiyor
İki noktada öküz
B(x1; 0) ve D(x2; 0), burada x1 ve x2
- Karekök
denklemler ax² + bx + c = 0.
B(x1; 0) noktası, burada x1 köktür
ikinci dereceden denklem.
3) çemberin ortak noktası yoktur
apsis eksenine sahip noktalar (Şekil 6, c), içinde
Bu durumda denklem olmaz
çözümler.

9. YÖNTEM: Bir nomogram kullanarak ikinci dereceden denklemleri çözme.

Tablo XXII. s.83 (bkz. Bradis V.M. Dört haneli
matematiksel tablolar. - M., Aydınlanma,
1990).
Denklem Çözümü için Nomogram
z2 + pz + q = 0. Bu nomogram,
ikinci dereceden bir denklemi çözmeden,
Katsayılarına göre denklemin köklerini belirleyin.
Nomogramın eğrisel ölçeği oluşturulur
formüllere göre (Şekil 11):
z2 + pz + q = 0,
z harfi herhangi bir etiket anlamına gelir
kavisli ölçek noktaları.

10. YÖNTEM: Geometrik yol
ikinci dereceden denklemlerin çözümleri.
Eski Yunanlılar nasıl çözdü
denklem y2 + 6y - 16 = 0.
Çözüm şurada sunulmaktadır:
şekil, burada y2 + 6y = 16,
veya y2 + 6 y + 9 = 16 + 9.
y2 + 6y + 9 ve 16 + 9 ifadeleri
geometrik olarak temsil etmek
aynı kare ve
orijinal denklem y2 + 6y - 16
+ 9 - 9 = 0 - aynı
denklem. nereden alıyoruz
y + 3 = + 5 ve y + 3 = -5, veya
y=2, y2= -8
de
3
de
y2
3
3 yıl
3 yıl
9

işim bunu mümkün kılıyor
zorluklara bak
matematiğimiz var.
bu çözümler hak ediyor
dikkat
yansımadıkları için
okul matematik ders kitapları;
bu tekniklerde uzmanlaşmak bana yardımcı oluyor
zamandan tasarruf edin ve verimli bir şekilde çözün
denklemler;
hızlı bir çözüm ihtiyacı
bir test sisteminin kullanılması nedeniyle
Final sınavları;

Çözüm

“Matematikte, kişi hatırlamamalı
formüller değil, düşünce süreçleri"
Başkan Yardımcısı Ermakov

Kopyevskaya kırsal orta öğretim okulu

İkinci Dereceden Denklemleri Çözmenin 10 Yolu

Başkan: Patrikeeva Galina Anatolyevna,

matematik öğretmeni

s.Kopyevo, 2007

1. İkinci dereceden denklemlerin gelişiminin tarihi

1.1 Eski Babil'de ikinci dereceden denklemler

1.2 Diophantus ikinci dereceden denklemleri nasıl derledi ve çözdü?

1.3 Hindistan'da ikinci dereceden denklemler

1.4 Harezmi'deki ikinci dereceden denklemler

1.5 Avrupa XIII - XVII yüzyıllarda ikinci dereceden denklemler

1.6 Vieta teoremi hakkında

2. İkinci dereceden denklemleri çözme yöntemleri

Çözüm

Edebiyat

1. İkinci dereceden denklemlerin gelişim tarihi

1.1 Eski Babil'de ikinci dereceden denklemler

Eski zamanlarda sadece birinci değil, aynı zamanda ikinci dereceden denklemleri çözme ihtiyacı, askeri nitelikteki arazi ve toprak işlerinin yanı sıra astronomi ve bilimin gelişmesiyle ilgili sorunları çözme ihtiyacından kaynaklandı. matematiğin kendisi. İkinci dereceden denklemler yaklaşık MÖ 2000'i çözebildi. e. Babilliler.

Modern cebirsel gösterimi kullanarak, çivi yazısı metinlerinde, eksik olanlara ek olarak, örneğin tam ikinci dereceden denklemler olduğunu söyleyebiliriz:

X2 + X= ¾; X2 - X= 14,5

Babil metinlerinde belirtilen bu denklemleri çözme kuralı esasen modern olanla örtüşmektedir, ancak Babillilerin bu kurala nasıl geldiği bilinmemektedir. Şimdiye kadar bulunan hemen hemen tüm çivi yazılı metinler, nasıl bulunduklarına dair hiçbir belirti olmaksızın, yalnızca tarifler şeklinde belirtilen çözümlerle ilgili sorunları verir.

Babil'de cebirin yüksek düzeyde gelişmesine rağmen, çivi yazılı metinler negatif sayı kavramından ve ikinci dereceden denklemleri çözmek için genel yöntemlerden yoksundur.

1.2 Diophantus ikinci dereceden denklemleri nasıl derler ve çözer.

Diophantus'un Aritmetiği, cebirin sistematik bir açıklamasını içermez, ancak açıklamaların eşlik ettiği ve çeşitli derecelerde denklemler formüle ederek çözülen sistematik bir dizi problem içerir.

Diophantus denklemleri derlerken çözümü basitleştirmek için bilinmeyenleri ustaca seçer.

Burada, örneğin, görevlerinden biri.

Görev 11."Toplamlarının 20 ve çarpımlarının 96 olduğunu bilerek iki sayı bulun"

Diophantus şöyle tartışır: Problemin koşulundan, istenen sayıların eşit olmadığı sonucu çıkar, çünkü eğer eşit olsaydı, çarpımları 96'ya değil, 100'e eşit olurdu. toplamlarının yarısı, yani. 10+x, diğeri daha küçüktür, yani. 10'lar. Aralarındaki fark 2 kere.

Dolayısıyla denklem:

(10 + x)(10 - x) = 96

100'ler 2 = 96

X 2 - 4 = 0 (1)

Buradan x = 2. İstenilen numaralardan biri 12 , başka 8 . Çözüm x = -2 Diophantus diye bir şey yoktur, çünkü Yunan matematiği yalnızca pozitif sayıları biliyordu.

Bu problemi istenilen sayılardan birini bilinmeyen olarak seçerek çözersek denklemin çözümüne ulaşmış oluruz.

y(20 - y) = 96,

de2 - 20y + 96 = 0. (2)

Diophantus'un bilinmeyen olarak istenen sayıların yarı farkını seçerek çözümü basitleştirdiği açıktır; sorunu, tamamlanmamış bir ikinci dereceden denklemi (1) çözmeye indirgemeyi başarır.

1.3 Hindistan'da ikinci dereceden denklemler

İkinci dereceden denklemler için problemler, 499'da Hintli matematikçi ve astronom Aryabhatta tarafından derlenen astronomik yol "Aryabhattam" da zaten bulundu. Başka bir Hintli bilim adamı, Brahmagupta (7. yüzyıl), tek bir kanonik forma indirgenmiş ikinci dereceden denklemleri çözmek için genel kuralı özetledi:

ey2 + bx = c, a > 0. (1)

(1) numaralı denklemde, katsayılar, a, olumsuz da olabilir. Brahmagupta'nın kuralı esasen bizimkiyle örtüşür.

Eski Hindistan'da, zor sorunları çözmede halka açık yarışmalar yaygındı. Eski Hint kitaplarından birinde, bu tür yarışmalar hakkında şöyle söylenir: "Güneş, parlaklığıyla yıldızları gölgede bırakıyorsa, bilgili bir kişi de halka açık toplantılarda, cebirsel problemleri önererek ve çözerek bir başkasının görkemini gölgede bırakacaktır." Görevler genellikle şiirsel bir biçimde giyinirdi.

İşte XII.Yüzyılın ünlü Hintli matematikçisinin sorunlarından biri. Bhaskara.

Görev 13.

"Ukala bir maymun sürüsü Ve asmalarda on iki...

Güç yemiş, eğlenmiş. Atlamaya başladılar, asılı kaldılar ...

Sekizinci bölüm bir meydanda Kaç maymun vardı,

Çayırda eğlenmek. Bana bu sürüde mi söylüyorsun?

Bhaskara'nın çözümü, ikinci dereceden denklemlerin köklerinin iki değerliliğini bildiğini gösterir (Şekil 3).

13. probleme karşılık gelen denklem:

(x/8) 2 + 12 = x

Bhaskara kisvesi altında yazıyor:

X2 - 64x = -768

ve bu denklemin sol tarafını bir kareye tamamlamak için her iki tarafa da ekler 32 2 , o zaman almak:

X2 - 64x + 322 = -768 + 1024,

(x - 32)2 = 256,

x - 32 = ± 16,

X1 = 16, x2 = 48.

1.4 El-Khorezmi'de ikinci dereceden denklemler

Al-Khorezmi'nin cebirsel incelemesi, doğrusal ve ikinci dereceden denklemlerin bir sınıflandırmasını verir. Yazar, bunları aşağıdaki gibi ifade eden 6 tür denklemi listeler:

1) "Kareler köklere eşittir", yani. ey2 + ile =bX.

2) "Kareler sayıya eşittir", yani. ey2 = s.

3) "Kökler sayıya eşittir", yani. ah = s.

4) "Kareler ve sayılar köklere eşittir", yani. ey2 + ile =bX.

5) "Kareler ve kökler sayıya eşittir", yani. ey2 + sevgili= s.

6) "Kökler ve sayılar karelere eşittir", yani.sevgili+ c = balta2 .

Negatif sayıları kullanmaktan kaçınan el-Harezmi için, bu denklemlerin her birinin terimleri çıkarma değil toplamadır. Bu durumda, pozitif çözümü olmayan denklemler açıkça dikkate alınmaz. Yazar, el-cebr ve el-mukabele yöntemlerini kullanarak bu denklemleri çözme yöntemlerini ortaya koymaktadır. Onun kararları elbette bizimkilerle tamamen örtüşmüyor. Tamamen retorik olduğu gerçeğinden bahsetmiyorum bile, örneğin, birinci tip eksik bir ikinci dereceden denklemi çözerken not edilmelidir.

El-Khorezmi, 17. yüzyıldan önceki tüm matematikçiler gibi, muhtemelen belirli pratik problemlerde önemli olmadığı için sıfır çözümü hesaba katmaz. Al - Khorezmi'nin tam ikinci dereceden denklemlerini kısmi olarak çözerken sayısal örnekler karar kurallarını ve ardından geometrik kanıtları belirler.

Görev 14.“Kare ve 21 sayısı 10 köke eşittir. Kökünü bulun" (x denkleminin kökünü varsayarsak2 + 21 = 10x).

Yazarın çözümü şuna benzer: kök sayısını ikiye bölün, 5 elde edin, 5'i kendisiyle çarpın, üründen 21 çıkarın, 4 kalır 4'ün kökünü alın, 2'yi 5'ten çıkarın, siz 3 olsun, bu istenen kök olacaktır. Veya 2'ye 5 ekleyin, bu da 7 verecek, bu da bir kök.

Risale-i Harezmi, ikinci dereceden denklemlerin sınıflandırılmasının sistematik olarak belirtildiği ve çözüm formüllerinin verildiği, bize ulaşan ilk kitaptır.

1.5 Avrupa'da ikinci dereceden denklemlerXIII- XVIIyüzyıllar

Avrupa'daki el-Khorezmi modeli üzerinde ikinci dereceden denklemleri çözmek için formüller ilk olarak 1202'de İtalyan matematikçi Leonardo Fibonacci tarafından yazılan "Abaküs Kitabı"nda ortaya kondu. Matematiğin etkisini yansıtan bu hacimli eser, gerek İslam ülkelerinde gerekse Antik Yunan, sunumun hem eksiksizliği hem de netliği bakımından farklılık gösterir. Yazar bağımsız olarak bazı yeni cebirsel problem çözme örnekleri geliştirdi ve Avrupa'da negatif sayıların kullanımına ilk yaklaşan kişi oldu. Kitabı cebirsel bilginin sadece İtalya'da değil, Almanya, Fransa ve diğer Avrupa ülkelerinde de yayılmasına katkıda bulundu. "Abaküs Kitabı" ndan birçok görev, 16. - 17. yüzyılların neredeyse tüm Avrupa ders kitaplarına geçti. ve kısmen XVIII.

SAYFA SONU--

Tek bir kanonik forma indirgenmiş ikinci dereceden denklemleri çözmek için genel kural:

X2 + sevgili= ile,

katsayıların tüm olası işaret kombinasyonları için b, İle birlikte Avrupa'da sadece 1544'te M. Stiefel tarafından formüle edilmiştir.

Vieta, ikinci dereceden bir denklemi çözmek için formülün genel bir türevine sahiptir, ancak Vieta yalnızca pozitif kökleri tanıdı. İtalyan matematikçiler Tartaglia, Cardano, Bombelli, 16. yüzyılda ilk olanlar arasındaydı. Olumlu ve olumsuz köklere ek olarak dikkate alın. Sadece XVII yüzyılda. Girard, Descartes, Newton ve diğer bilim adamlarının çalışmaları sayesinde ikinci dereceden denklemleri çözmenin yolu modern bir görünüm kazanıyor.

1.6 Vieta teoremi hakkında

İkinci dereceden bir denklemin katsayıları ile kökleri arasındaki ilişkiyi ifade eden Vieta adını taşıyan teorem, ilk kez 1591 yılında kendisi tarafından şu şekilde formüle edilmiştir: B+ Dçarpılır A- A2 , eşittir BD, sonra A eşittir AT ve eşit D».

Vieta'yı anlamak için şunu unutmamak gerekir. ANCAK, herhangi bir sesli harf gibi, onun için bilinmeyen anlamına geliyordu (bizim X), Sesli harfler AT,D- bilinmeyen için katsayılar. Modern cebir dilinde, Vieta'nın yukarıdaki formülasyonu şu anlama gelir: eğer

(bir +b)x - x2 = ab,

X2 - (bir +b)x + birb= 0,

X1 = bir, x2 = b.

Denklemlerin kökleri ve katsayıları arasındaki ilişkiyi ifade etme genel formüller, semboller kullanılarak yazılan Viet, denklemleri çözme yöntemlerinde tekdüzelik kurdu. Ancak, Vieta'nın sembolizmi hala modern görünüm. Negatif sayıları tanımıyordu ve bu nedenle denklemleri çözerken sadece tüm köklerin pozitif olduğu durumları düşündü.

2. İkinci dereceden denklemleri çözme yöntemleri

İkinci dereceden denklemler, cebirin görkemli yapısının dayandığı temeldir. İkinci dereceden denklemler, trigonometrik, üstel, logaritmik, irrasyonel ve aşkın denklemlerin ve eşitsizliklerin çözümünde yaygın olarak kullanılmaktadır. Hepimiz okuldan (8. sınıf) mezuniyete kadar ikinci dereceden denklemleri nasıl çözeceğimizi biliyoruz.

Okul matematik dersinde, herhangi bir ikinci dereceden denklemi çözebileceğiniz, ikinci dereceden denklemlerin köklerinin formülleri incelenir. Bununla birlikte, birçok denklemi çok hızlı ve rasyonel olarak çözmenize izin veren ikinci dereceden denklemleri çözmenin başka yolları da vardır. İkinci dereceden denklemleri çözmenin on yolu vardır. Çalışmamda her birini ayrıntılı olarak analiz ettim.

1. YÖNTEM : Denklemin sol tarafının çarpanlara ayrılması.

denklemi çözelim

X2 + 10x - 24 = 0.

Sol tarafı çarpanlarına ayıralım:

X2 + 10x - 24 = x2 + 12x - 2x - 24 \u003d x (x + 12) - 2 (x + 12) \u003d (x + 12) (x - 2).

Bu nedenle, denklem şu şekilde yeniden yazılabilir:

(x + 12)(x - 2) = 0

Çarpım sıfır olduğundan, faktörlerinden en az biri sıfırdır. Bu nedenle, denklemin sol tarafı kaybolur x = 2, aynı zamanda x = - 12. Bunun anlamı, sayı 2 ve - 12 denklemin kökleri X2 + 10x - 24 = 0.

2. YÖNTEM : Tam kare seçim yöntemi.

denklemi çözelim X2 + 6x - 7 = 0.

Sol tarafta tam bir kare seçelim.

Bunu yapmak için x2 + 6x ifadesini aşağıdaki biçimde yazıyoruz:

X2 + 6x = x2 + 2x3.

Ortaya çıkan ifadede, ilk terim x sayısının karesidir ve ikincisi x'in 3'ün çift çarpımıdır. Bu nedenle, tam kareyi elde etmek için 32 eklemeniz gerekir, çünkü

x2 + 2x3 + 32 = (x + 3)2 .

Şimdi denklemin sol tarafını dönüştürüyoruz

X2 + 6x - 7 = 0,

buna ekleme ve çıkarma 32. Bizde:

X2 + 6x - 7 = x2 + 2x3 + 32 - 3 2 - 7 = (x + 3)2 - 9 - 7 = (x + 3)2 - 16.

Böylece, bu denklem aşağıdaki gibi yazılabilir:

(x + 3)2 - 16 = 0, (x + 3)2 = 16.

Sonuç olarak, x + 3 - 4 = 0, x1 = 1 veya x + 3 = -4, x2 = -7.

3. YÖNTEM :İkinci dereceden denklemlerin formülle çözümü.

Denklemin her iki tarafını da çarpın

ey2 + bx + c = 0, a ≠ 0

4a'da ve art arda elimizde:

4a2 X2 + 4abx + 4ac = 0,

((2ah)2 + 2axb+ b2 ) - b2 + 4 AC= 0,

(2ax+b)2 = b2 - 4ac,

2ax + b = ± √ b2 - 4ac,

2ax = - b ± √ b2 - 4ac,

Örnekler.

a) Denklemi çözelim: 4x2 + 7x + 3 = 0.

bir = 4,b= 7, c = 3,D= b2 - 4 AC= 7 2 - 4 4 3 = 49 - 48 = 1,

D> 0, iki farklı kökler;

Böylece, pozitif bir ayrımcı durumunda, yani. de

b2 - 4 AC>0 , denklem ey2 + bx + c = 0 iki farklı kökü vardır.

b) Denklemi çözelim: 4x2 - 4x + 1 = 0,

bir = 4,b= - 4, c = 1,D= b2 - 4 AC= (-4) 2 - 4 4 1= 16 - 16 = 0,

D= 0, bir kök;

Yani, eğer diskriminant sıfır ise, yani. b2 - 4 AC= 0 , sonra denklem

ey2 + bx + c = 0 tek bir kökü var

içinde) Denklemi çözelim: 2 kere2 + 3x + 4 = 0,

bir = 2,b= 3, c = 4,D= b2 - 4 AC= 3 2 - 4 2 4 = 9 - 32 = - 13, D< 0.

devam
--SAYFA SONU--

Bu denklemin kökü yoktur.

Yani, eğer diskriminant negatif ise, yani. b2 - 4 AC< 0 ,

denklem ey2 + bx + c = 0 kökleri yoktur.

İkinci dereceden denklemin köklerinin formülü (1) ey2 + bx + c = 0 kökleri bulmanızı sağlar hiç ikinci dereceden denklem (varsa), indirgenmiş ve eksik dahil. Formül (1) sözlü olarak şu şekilde ifade edilir: ikinci dereceden bir denklemin kökleri, payı, zıt işaretle alınan ikinci katsayıya eşit olan bir kesre eşittir, artı eksi bu katsayının karesinin karekökü, serbest terimle ilk katsayının ürününü dört katına çıkarmadan, ve payda birinci katsayının iki katıdır.

4. YÖNTEM: Vieta teoremini kullanarak denklemlerin çözümü.

Bilindiği gibi, verilen ikinci dereceden denklem forma sahiptir

X2 + piksel+ c= 0. (1)

Kökleri Vieta teoremini tatmin eder; a=1 forma sahip

/>x1 x2 = q,

x1 + x2 = - p

Bundan aşağıdaki sonuçları çıkarabiliriz (köklerin işaretleri p ve q katsayılarından tahmin edilebilir).

a) Özet terim ise q indirgenmiş denklem (1) pozitiftir ( q> 0 ), o zaman denklemin aynı işaretin iki kökü vardır ve bu ikinci katsayının kıskançlığıdır. p. Eğer bir R< 0 , o zaman her iki kök de negatifse R< 0 , o zaman her iki kök de pozitiftir.

Örneğin,

x2 – 3 x+ 2 = 0; x1 = 2 ve x2 = 1, çünkü q= 2 > 0 ve p= - 3 < 0;

x2 + 8 x+ 7 = 0; x1 = - 7 ve x2 = - 1, çünkü q= 7 > 0 ve p= 8 > 0.

b) Ücretsiz üye ise q indirgenmiş denklem (1) negatiftir ( q< 0 ), o zaman denklemin farklı işaretli iki kökü vardır ve eğer mutlak değerdeki daha büyük kök pozitif olacaktır: p< 0 veya olumsuz ise p> 0 .

Örneğin,

x2 + 4 x– 5 = 0; x1 = - 5 ve x2 = 1, çünkü q= - 5 < 0 ve p= 4 > 0;

x2 – 8 x– 9 = 0; x1 = 9 ve x2 = - 1, çünkü q= - 9 < 0 ve p= - 8 < 0.

5. YÖNTEM: "Transfer" yöntemini kullanarak denklemleri çözme.

İkinci dereceden denklemi düşünün

ey2 + bx + c = 0, nerede bir ≠ 0.

Her iki parçasını da a ile çarparak denklemi elde ederiz.

a2 X2 + birbx + ac = 0.

İzin vermek ah = y, nerede x = y/a; sonra denkleme geliyoruz

de2 + ile+ ac = 0,

buna eşdeğer. kökleri de1 ve de 2, Vieta teoremi kullanılarak bulunabilir.

sonunda anladık

X1 = y1 /a ve X1 = y2 /a.

Bu yöntemle katsayı a serbest terimle çarpılır, sanki ona "atılmış" gibi, buna denir transfer yöntemi. Bu yöntem, Vieta teoremini kullanarak bir denklemin köklerini bulmak kolay olduğunda ve en önemlisi, diskriminant tam bir kare olduğunda kullanılır.

Örnek.

denklemi çözelim 2 kere2 – 11x + 15 = 0.

Çözüm. 2 katsayısını serbest terime "aktaralım", sonuç olarak denklemi elde ederiz.

de2 – 11y + 30 = 0.

Vieta teoremine göre

/>/>/>/>/>de1 = 5x1 = 5/2 x1 = 2,5

de2 = 6 x2 = 6/2 x2 = 3.

Cevap: 2.5; 3.

6. YÖNTEM: İkinci dereceden bir denklemin katsayılarının özellikleri.

ANCAK. ikinci dereceden denklem olsun

ey2 + bx + c = 0, nerede bir ≠ 0.

1) Eğer, bir+b+ c = 0 (yani katsayıların toplamı sıfırdır), sonra x1 = 1,

X2 = s/a.

Kanıt. Denklemin her iki tarafını da ≠ 0'a bölersek, indirgenmiş ikinci dereceden denklemi elde ederiz.

x2 + b/ a x+ c/ a= 0.

/>Vieta teoremine göre

x1 + x2 = - b/ a,

x1 x2 = 1 c/ a.

koşula göre a -b+ c = 0, nerede b= a + c. Böylece,

/>x1 + x2 = - a+ b / a \u003d -1 - c / a,

x1 x2 = - 1 (-c/a),

şunlar. X1 = -1 ve X2 = c/ a, ki kanıtlamamız gerekiyordu.

Örnekler

denklemi çözelim 345x2 - 137x - 208 = 0.

Çözüm.Çünkü bir +b+ c \u003d 0 (345 - 137 - 208 \u003d 0), sonra

X1 = 1, x2 = c/ a= -208/345.

Cevap 1; -208/345.

2) Denklemi çözün 132x2 – 247x + 115 = 0.

Çözüm.Çünkü bir +b+ c \u003d 0 (132 - 247 + 115 \u003d 0), sonra

X1 = 1, x2 = c/ a= 115/132.

Cevap 1; 115/132.

B. ikinci katsayı ise b= 2 k– çift sayı, sonra köklerin formülü

devam
--SAYFA SONU--

Örnek.

denklemi çözelim 3x2 - 14x + 16 = 0.

Çözüm. Sahibiz: bir = 3,b= - 14, c = 16,k= - 7 ;

D= k2 – AC= (- 7) 2 – 3 16 = 49 – 48 = 1, D> 0, iki farklı kök;

Cevap: 2; 8/3

AT. İndirgenmiş Denklem

X2 +px+q= 0

genel denklemle örtüşür, ki burada bir = 1, b= p ve c =q. Bu nedenle, indirgenmiş ikinci dereceden denklem için, köklerin formülü

formu alır:

Formül (3) özellikle aşağıdaki durumlarda kullanımı uygundur: R- çift sayı.

Örnek. denklemi çözelim X2 – 14x – 15 = 0.

Çözüm. Sahibiz: X1,2 =7±

Cevap: x1 = 15; X2 = -1.

7. YÖNTEM: İkinci dereceden bir denklemin grafik çözümü.

denklemde ise

X2 + piksel+ q= 0

ikinci ve üçüncü terimleri sağa kaydırırsak

X2 = - piksel- q.

y \u003d x2 ve y \u003d - px - q bağımlılık grafikleri oluşturalım.

İlk bağımlılığın grafiği, orijinden geçen bir paraboldür. İkinci bağımlılığın grafiği -

düz çizgi (Şekil 1). Aşağıdaki durumlar mümkündür:

Düz bir çizgi ve bir parabol iki noktada kesişebilir, kesişme noktalarının apsisleri ikinci dereceden bir denklemin kökleridir;

Doğru ve parabol birbirine değebilir (sadece bir ortak nokta), yani. denklemin bir çözümü vardır;

Düz çizgi ve parabolün ortak noktaları yoktur, yani. ikinci dereceden bir denklemin kökü yoktur.

Örnekler

1) Denklemi grafiksel olarak çözelim X2 - 3x - 4 = 0(İncir. 2).

Çözüm. Denklemi formda yazıyoruz X2 = 3x + 4.

Bir parabol oluşturalım y = x2 ve doğrudan y = 3x + 4. doğrudan

y = 3x + 4 iki noktadan inşa edilebilir M (0; 4) ve

N(3; 13) . Bir doğru ve bir parabol iki noktada kesişir

ANCAK ve AT apsisli X1 = - 1 ve X2 = 4 . Cevap : X1 = - 1;

X2 = 4.

2) Denklemi grafiksel olarak çözelim (Şekil 3) X2 - 2x + 1 = 0.

Çözüm. Denklemi formda yazıyoruz X2 = 2x - 1.

Bir parabol oluşturalım y = x2 ve doğrudan y = 2x - 1.

doğrudan y = 2x - 1 iki nokta üzerine inşa M (0; - 1)

ve N(1/2; 0) . Doğru ve parabol bir noktada kesişir ANCAKİle birlikte

apsis x = 1. Cevap: x = 1.

3) Denklemi grafiksel olarak çözelim X2 - 2x + 5 = 0(Şek. 4).

Çözüm. Denklemi formda yazıyoruz X2 = 5x - 5. Bir parabol oluşturalım y = x2 ve doğrudan y = 2x - 5. doğrudan y = 2x - 5 iki nokta M(0; - 5) ve N(2.5; 0) ile oluşturun. Düz çizgi ve parabolün kesişme noktaları yoktur, yani. Bu denklemin kökü yoktur.

Cevap. denklem X2 - 2x + 5 = 0 kökleri yoktur.

8. YÖNTEM: İkinci dereceden denklemleri pusula ve cetvelle çözme.

Bir parabol kullanarak ikinci dereceden denklemleri çözmenin grafik yolu elverişsizdir. Nokta nokta bir parabol oluşturursanız, çok zaman alır ve elde edilen sonuçların doğruluk derecesi düşüktür.

İkinci dereceden bir denklemin köklerini bulmak için aşağıdaki yöntemi öneriyorum ey2 + bx + c = 0 pusula ve cetvel kullanarak (Şek. 5).

İstenen dairenin ekseni kestiğini varsayalım.

noktalarda apsis B(x1 ; 0) ve D(X2 ; 0), nerede X1 ve X2 - denklemin kökleri ey2 + bx + c = 0, ve noktalardan geçer

bir(0; 1) ve C(0;c/ a) y ekseninde. O halde, sekant teoremine göre, OB OD= AE OK, nerede OK= OB OD/ AE= x1 X2 / 1 = c/ a.

Dairenin merkezi, diklerin kesişme noktasındadır. bilimkurgu ve SK, akorların orta noktalarında restore AC ve BD, bu yüzden

1) noktalar oluşturun (dairenin merkezi) ve A(0; 1) ;

2) yarıçaplı bir daire çizin SA;

3) bu dairenin eksen ile kesişme noktalarının apsisi ey orijinal ikinci dereceden denklemin kökleridir.

Bu durumda, üç durum mümkündür.

1) Çemberin yarıçapı, merkezin koordinatından büyük (OLARAK> SK, veyaR> a+ c/2 a) , daire x eksenini iki noktada kesiyor (Şekil 6, a) B(x1 ; 0) ve D(X2 ; 0) , nerede X1 ve X2 - ikinci dereceden denklemin kökleri ey2 + bx + c = 0.

2) Dairenin yarıçapı, merkezin ordinatına eşittir (OLARAK= SB, veyaR= a+ c/2 a) , daire Ox eksenine (Şekil 6, b) noktasında temas eder. B(x1 ; 0) , burada x1 ikinci dereceden denklemin köküdür.

devam
--SAYFA SONU--

3) Dairenin yarıçapı, merkezin ordinatından daha küçüktür, dairenin apsis ekseni ile ortak noktası yoktur (Şekil 6, c), bu durumda denklemin bir çözümü yoktur.

Örnek.

denklemi çözelim X2 - 2x - 3 = 0(Şek. 7).

Çözüm. Dairenin merkezinin noktasının koordinatlarını formüllerle belirleyin:

A (0; 1) olmak üzere SA yarıçaplı bir daire çizelim.

Cevap:X1 = - 1; X2 = 3.

9. YÖNTEM: Bir nomogram kullanarak ikinci dereceden denklemleri çözme.

Bu, ikinci dereceden denklemleri çözmek için 83. sayfada yer alan eski ve haksız yere unutulmuş bir yöntemdir (bkz. Bradis V.M. Dört basamaklı matematiksel tablolar. - M., Enlightenment, 1990).

Tablo XXII. Denklem Çözümü için Nomogram z2 + pz+ q= 0 . Bu nomogram, ikinci dereceden denklemi çözmeden denklemin köklerini katsayılarıyla belirlemeye izin verir.

Nomogramın eğrisel ölçeği, formüllere göre oluşturulmuştur (Şekil 11):

varsayarsak işletim sistemi = p,ED= q, OE = bir(hepsi cm cinsinden), üçgenlerin benzerliğinden SAN ve CDF oranı elde ederiz

ikameler ve sadeleştirmelerden sonra denklem aşağıdaki gibidir:

z2 + pz+ q= 0,

ve mektup z eğri ölçekte herhangi bir noktanın etiketi anlamına gelir.

Örnekler

1) denklem için z2 - 9 z+ 8 = 0 nomogram kök verir

z1 = 8,0 ve z2 = 1,0 (Şek. 12).

2) Denklemi nomogramı kullanarak çözüyoruz

2 z2 - 9 z+ 2 = 0.

Bu denklemin katsayılarını 2'ye bölersek denklemi elde ederiz.

z2 - 4,5 z+ 1 = 0.

Nomogram kök verir z1 = 4 ve z2 = 0,5.

3) denklem için

z2 - 25 z+ 66 = 0

p ve q katsayıları ölçek dışı, ikameyi yapacağız z= 5 t, denklemi elde ederiz

t2 - 5 t+ 2,64 = 0,

bir nomogram aracılığıyla çözdüğümüz ve elde ettiğimiz t1 = 0,6 ve t2 = 4,4, nerede z1 = 5 t1 = 3,0 ve z2 = 5 t2 = 22,0.

10. YÖNTEM: İkinci dereceden denklemleri çözmenin geometrik yolu.

Geometrinin cebirden daha gelişmiş olduğu eski zamanlarda, ikinci dereceden denklemler cebirsel olarak değil geometrik olarak çözülürdü. Harezmi'nin "Cebir"inden meşhur olmuş bir örnek vereceğim.

Örnekler

1) Denklemi çözün X2 + 10x = 39.

Orijinalde bu problem şu şekilde formüle edilmiştir: “Kare ve on kök 39'a eşittir” (Şek. 15).

Çözüm. Kenarı x olan bir kare düşünün, kenarlarına dikdörtgenler inşa edilir, böylece her birinin diğer tarafı 2,5 olur, bu nedenle her birinin alanı 2,5x'tir. Ortaya çıkan şekil daha sonra köşelerde dört eşit kareyi tamamlayan yeni bir ABCD karesine eklenir, her birinin kenarı 2.5 ve alanı 6.25'tir.

Meydan S Meydan ABCD alanların toplamı olarak temsil edilebilir: orijinal kare X2 , dört dikdörtgen (4 2.5x = 10x) ve dört ekli kare (6,25 4 = 25) , yani S= X2 + 10x + 25. değiştirme

X2 + 10x sayı 39 , anladık S= 39 + 25 = 64 , buradan karenin kenarının ABCD, yani çizgi segmenti AB = 8. İstenilen taraf için X elde ettiğimiz orijinal kare

2) Ama, örneğin, eski Yunanlılar denklemi nasıl çözdüler? de2 + 6y - 16 = 0.

ÇözümŞek. 16, nerede

de2 + 6y = 16 veya y2 + 6y + 9 = 16 + 9.

Çözüm.İfade de2 + 6y + 9 ve 16 + 9 geometrik olarak aynı kareyi temsil eder ve orijinal denklem de2 + 6y - 16 + 9 - 9 = 0 aynı denklemdir. bunu nerden anlıyoruz y + 3 = ± 5, veya de1 = 2, y2 = - 8 (Şek. 16).

3) Geometrik denklemi çözün de2 - 6y - 16 = 0.

Denklemi dönüştürürsek,

de2 - 6y = 16.

Şek. 17 ifadenin "görüntülerini" bulun de2 - 6u,şunlar. y kenarı olan bir karenin alanından, kenarı eşit olan bir karenin alanının iki katını çıkarın 3 . Yani, eğer ifade de2 - 6y Ekle 9 , sonra bir kenarı olan bir karenin alanını elde ederiz y - 3. ifadenin değiştirilmesi de2 - 6y eşit sayı 16,

elde ederiz: (y - 3)2 = 16 + 9, şunlar. y - 3 = ± √25, veya y - 3 = ± 5, burada de1 = 8 ve de2 = - 2.

Çözüm

İkinci dereceden denklemler, trigonometrik, üstel, logaritmik, irrasyonel ve aşkın denklemlerin ve eşitsizliklerin çözümünde yaygın olarak kullanılmaktadır.

Bununla birlikte, ikinci dereceden denklemlerin değeri, çok önemli olmasına rağmen, sadece problem çözmenin zarafetinde ve kısalığında yatmıyor. İkinci dereceden denklemlerin problem çözmede kullanılmasının bir sonucu olarak, genellikle yeni detayların keşfedilmesi, elde edilen formüllerin ve ilişkilerin bir analiziyle yönlendirilen ilginç genellemeler yapılabileceği ve iyileştirmeler yapılabileceği gerçeği daha az önemli değildir.

Ayrıca, bu çalışmada sunulan konunun hala çok az çalışıldığını, sadece onunla ilgilenmediklerini, bu nedenle birçok gizli ve bilinmeyenle dolu olduğunu, bu da için mükemmel bir fırsat sağladığını belirtmek isterim. daha fazla çalışma onun üstünde.

Burada ikinci dereceden denklemleri çözme sorusuna karar verdim ve ne,

bunları çözmenin başka yolları varsa?! Yine güzel kalıplar, bazı gerçekler, açıklamalar bulun, genellemeler yapın, yeni ve yeni olan her şeyi keşfedin. Ancak bunlar gelecekteki çalışmalar için sorular.

Özetle, şu sonuca varabiliriz: ikinci dereceden denklemler matematiğin gelişiminde büyük rol oynar. Hepimiz okuldan (8. sınıf) mezuniyete kadar ikinci dereceden denklemleri nasıl çözeceğimizi biliyoruz. Bu bilgi yaşam boyunca bizim için yararlı olabilir.

İkinci dereceden denklemleri çözmek için bu yöntemlerin kullanımı kolay olduğundan, matematiğe düşkün öğrencilerin kesinlikle ilgisini çekmelidir. Çalışmam, matematiğin önümüze koyduğu problemlere farklı bir açıdan bakmayı mümkün kılıyor.

Edebiyat:

1. Alimov Ş.A., İlyin V.A. ve diğerleri Cebir, 6-8. 6-8 sınıf lise için deneme ders kitabı. - M., Eğitim, 1981.

2. bradis VM Lise için dört basamaklı matematik tabloları Ed. 57. - M., Eğitim, 1990. S. 83.

3. Kruzhepov A.K., Rubanov A.T. Cebir ve temel fonksiyonlar üzerine problemli kitap. İkincil uzmanlaşmış eğitim kurumları için ders kitabı. - M., lise, 1969.

4. Okunev A.K. İkinci dereceden fonksiyonlar, denklemler ve eşitsizlikler. Öğretmen için bir rehber. - M., Eğitim, 1972.

5. Presman A.A. Pusula ve cetvelle ikinci dereceden bir denklemi çözme. - M., Kvant, No. 4/72. 34.

6. Solomnik V.S., Milov P.I. Matematikte soru ve görevlerin toplanması. Ed. - 4, ekle. - M., Yüksek Okul, 1973.

7. Khudobin A.I. Cebir ve temel fonksiyonlarda problemlerin toplanması. Öğretmen için bir rehber. Ed. 2. - M., Eğitim, 1970.

https://pandia.ru/text/78/082/images/image002_237.gif" height="952"> MOU "Sergievskaya Ortaokulu"

Hazırlayan: Sizikov Stanislav

Öğretmen:

İle birlikte. Sergievka, 2007

1. Giriş. Eski Babil'de İkinci Dereceden Denklemler……………….3

2. Diaphant'ta ikinci dereceden denklemler…………..………………………….4

3. Hindistan'da ikinci dereceden denklemler ……………………………………………………………………………………………………………… …………………………………………………………………

4. El-Harezmi'de ikinci dereceden denklemler ……………………………………..6

5. Avrupa'da İkinci Dereceden Denklemler XIII - XYII……………………………...7

6. Vieta teoremi hakkında …………………………………………………………..9

7. İkinci dereceden denklemleri çözmenin on yolu……………………..10

8. Sonuç ………………………………………………………………20

9. Kaynaklar …………………………………………………….21

giriiş

ikinci dereceden denklemler

İkinci dereceden denklemler, cebirin görkemli yapısının dayandığı temeldir. İkinci dereceden denklemler, trigonometrik, üstel, logaritmik, irrasyonel denklemler. Hepimiz 8. sınıftan başlayarak ikinci dereceden denklemlerin nasıl çözüleceğini biliyoruz. Fakat ikinci dereceden denklemleri çözme tarihi nasıl ortaya çıktı ve gelişti?

Eski Babil'de İkinci Dereceden Denklemler

Sadece birinci değil, aynı zamanda ikinci dereceden denklemleri antik çağda çözme ihtiyacı, arazi alanlarını bulma ile ilgili problemleri çözme ihtiyacından kaynaklandı; askeri nitelikteki toprak işleri ile astronomi ve matematiğin kendisinin gelişimi. İkinci dereceden denklemler yaklaşık MÖ 2000'i çözebildi. e. Babilliler. Modern cebirsel gösterimi kullanarak, çivi yazısı metinlerinde eksik olanlara ek olarak, örneğin tam ikinci dereceden denklemler olduğunu söyleyebiliriz: x2 + x = , : x2 - x = 14https://pandia.ru/text /78/082 /images/image005_150.gif" width="16" height="41 src=">)2 + 12 = x; Bhaskara kisvesi altında yazar

x2- 64X = - 768

ve bu denklemin sol tarafını kareye tamamlamak için her iki tarafa da 322 ekler ve şu sonucu alır: x2- 64x + 322 = - 768 + 1024;

(X- 32)2 = 256; X - 32 = ± 16, xt = 16, hg= 48.

Al - Khorezmi'de ikinci dereceden denklemler

El-Khwarizmi'nin cebirsel incelemesi, doğrusal ve ikinci dereceden denklemlerin bir sınıflandırmasını verir. Yazar, bunları aşağıdaki gibi ifade eden 6 tür denklemi listeler:

1) "Kareler köklere eşittir", yani. ax2 = içinde.

2) “Kareler sayıya eşittir”, yani. ah2= İle birlikte.

3) "Kökler sayıya eşittir", yani. ah = s.

4) “Kareler ve sayılar köklere eşittir”, yani. ah2+ c = içinde.

5) “Kareler ve kökler sayıya eşittir”, yani. ah2+ içinde = s.

6) "Kökler ve sayılar karelere eşittir", yani. içinde+ c \u003d ax2. Negatif sayıları kullanmaktan kaçınan el-Harezmi için, bu denklemlerin her birinin terimleri çıkarma değil toplamadır. Bu durumda, pozitif çözümü olmayan denklemler açıkça dikkate alınmaz. Yazar, bu denklemleri çözmek için yöntemler ortaya koymaktadır. Onun kararı elbette bizimkiyle tamamen örtüşmüyor. Bunun tamamen retorik olduğu gerçeğinden bahsetmiyorum bile, örneğin, birinci türden tamamlanmamış ikinci dereceden bir denklemi çözerken, 17. yüzyıldan önceki tüm matematikçiler gibi, el-Harezmi'nin sıfırı hesaba katmadığı belirtilmelidir. çözüm, muhtemelen belirli pratik görevlerde önemli olmadığı için. Tam ikinci dereceden denklemleri çözerken, el-Khorezmi belirli sayısal örnekler kullanarak bunları çözme kurallarını ve ardından geometrik kanıtlarını belirler.

Bir örnek alalım.

Problem 14. “Kare ve 21 sayısı 10 köke eşittir. Kökü bulun "(denklemin kökü anlamına gelir) x2+ 21 = 10X).

El-Harezmi'nin incelemesi, ikinci dereceden denklemlerin sınıflandırılmasının sistematik olarak sunulduğu ve çözüm formüllerinin verildiği bize ulaşan ilk kitaptır.

Avrupa'da ikinci dereceden denklemlerXIII- XVIIyüzyıllar

Avrupa'daki el-Harezmi modeli üzerinde ikinci dereceden denklemleri çözmek için formüller ilk olarak "Abaküs Kitabı"nda (geçen yüzyılın ortalarında Roma'da yayınlanan, Fibonacci tarafından "Abaküs Kitabı" 459 içerir) ortaya konmuştur. 1202 yılında İtalyan matematikçi Leonardo Fibonacci tarafından yazılmıştır. Hem İslam ülkelerinden hem de Antik Yunanistan'dan matematiğin etkisini yansıtan bu hacimli eser, hem eksiksizliği hem de sunumun netliği ile ayırt edilir. Yazar bağımsız olarak problem çözmenin bazı yeni cebirsel örneklerini geliştirdi ve ilk içinde Avrupa, negatif sayıların getirilmesine yaklaştı. Kitabı cebirsel bilginin sadece İtalya'da değil, Almanya, Fransa ve diğer Avrupa ülkelerinde de yayılmasına katkıda bulundu. Abaküs Kitabı'ndaki birçok görev, 16.-17. yüzyılların neredeyse tüm Avrupa ders kitaplarına geçti. ve kısmen XVIII.

Tek bir kanonik forma indirgenmiş ikinci dereceden denklemleri çözmek için genel kural x2+ içinde = s, katsayıların tüm olası işaret kombinasyonları için ile Avrupa'da sadece 1544'te formüle edildi. M. Stiefel.

Vieta, ikinci dereceden bir denklemi çözmek için formülün genel bir türevine sahiptir, ancak Vieta yalnızca pozitif kökleri tanıdı. İtalyan matematikçiler Tartaglia, Cardaco, Bombelli 16. yüzyılda ilk olanlar arasındaydı. pozitif ve negatif köklere ek olarak dikkate alın. Sadece XVII yüzyılda. Girard, Descartes, Newton ve diğer bilim adamlarının çalışmaları sayesinde, ikinci dereceden denklemleri çözme yöntemi modern bir biçim alır.

Vieta teoremi hakkında

İkinci dereceden bir denklemin katsayıları ile kökleri arasındaki ilişkiyi ifade eden Vieta adını taşıyan teorem, ilk kez 1591 yılında kendisi tarafından şu şekilde formüle edilmiştir: AT+ D, çarpılır ANCAK eksi A2, eşittir BD, sonra ANCAK eşittir AT ve eşit D».

Vieta'yı anlamak için şunu unutmamak gerekir. ANCAK, herhangi biri gibi
sesli harf, onun için bilinmeyen (bizim X), sesli harfler
AT,D- bilinmeyen için katsayılar. Modern cebir dilinde, Vieta'nın yukarıdaki formülasyonu şu anlama gelir: eğer

(a+ c) x - x 2 = ab, x2 - (bir+ b) x + ab = 0, x1 = a, x2 = b.

Semboller kullanılarak yazılan genel formüllerle denklemlerin kökleri ve katsayıları arasındaki ilişkiyi ifade eden Viet, denklem çözme yöntemlerinde tekdüzelik kurdu. Bununla birlikte, Vieta'nın sembolizmi hala modern biçiminden uzaktır. Negatif sayıları tanımıyordu ve bu nedenle denklemleri çözerken sadece tüm köklerin pozitif olduğu durumları dikkate aldı.

İkinci Dereceden Denklemleri Çözmenin On Yolu

1. Denklemin sol tarafının çarpanlara ayrılması

denklemi çözelim x2+ 10X- 24 = 0. Denklemin sol tarafını çarpanlarına ayıralım:

x2 + 10x - 24 = x2 + 12x - 2x - 24 =

X(x + x + 12) = (x + 12)(x - 2).

Bu nedenle, denklem şu şekilde yeniden yazılabilir:

( X + 12)(x - 2) = 0.

Çarpım sıfır olduğu için çarpanlarından en az biri sıfırdır. Bu nedenle, denklemin sol tarafı kaybolduğunda x = 2, ayrıca X= - 12. Bu, 2 ve - 12 sayılarının x2 + 10x - 24 = 0 denkleminin kökleri olduğu anlamına gelir.

2. Tam kare seçim yöntemi

Bu yöntemi bir örnekle açıklayalım.

x2 + 6x - 7 = 0 denklemini çözelim. Sol taraftan bir tam kare seçin. Bunu yapmak için x2 + 6x ifadesini aşağıdaki biçimde yazıyoruz:

x2 + 6x = x2 + 2*x*3.

Ortaya çıkan ifadede, ilk terim x sayısının karesidir ve ikincisi x'in 3'ün çift çarpımıdır. Bu nedenle, tam kareyi elde etmek için 32 eklemeniz gerekir, çünkü

x2 + 2 x 3 + 32 = (x + 3)2.

Şimdi denklemin sol tarafını dönüştürüyoruz

x2 + 6x - 7 = 0,

buna ekleme ve çıkarma 32. Bizde:

x2 + 6x - 7 = x2 + 2 X 3 +– 7 = (X- \u003d (x - Z) 2 - 16 .

Böylece, bu denklem aşağıdaki gibi yazılabilir:

(x + = 0, yani (x + 3)2 = 16.

Sonuç olarak, X+ 3 \u003d 4 x1 \u003d 1 veya x + 3 \u003d - 4, x2 \u003d - 7.

3. İkinci dereceden denklemlerin formülle çözümü

Denklemin her iki tarafını da çarpın

ah2+ içinde+ c = 0, bir ≠ 0, açık 4a ve art arda elimizde:

4a2 x2 + 4abx+ 4ac = 0,

((2ax)2 + 2 balta + b2 ) - b2 + 4ac= 0,

(2aks +b)2 = in2- 4ac,

2ax+ b= ± https://pandia.ru/text/78/082/images/image006_128.gif" width="71" height="27">, x1,2 =

Bir pozitif ayrımcı durumunda, yani v2 - 4ac > 0, denklem ah2+ + s içinde= 0'ın iki farklı kökü vardır.

Diskriminant sıfır ise, yani. v2 - 4ac = 0, sonra denklem ah2+ içinde+ İle birlikte= 0'ın tek bir kökü vardır, x = - https://pandia.ru/text/78/082/images/image009_95.gif" width="14" height="62"> Kökleri Vieta teoremini karşılar; ne zaman a= 1 formu var

x1 x2 = q,

x1 + x2 = - R.

Bundan aşağıdaki sonuçları çıkarabiliriz (katsayılarla R ve q kök işaretleri tahmin edilebilir).

a) Ücretsiz üye ise q indirgenmiş denklem (1)
pozitif (q> 0), o zaman denklemin iki özdeş
kökün işareti ile ve ikinci katsayıya bağlıdır R
Eğer bir R> 0, o zaman her iki kök de negatifse R< 0, o zaman ikisi de
kökler pozitiftir.

Örneğin,

x2- 3X + 2 = 0; x1= 2 ve x2 = 1, çünkü q = 2 > 0 sen p = - 3 < 0;

x2 + 8x + 7 = 0; x 1 \u003d - 7 ve x2 \u003d - 1, çünkü q= 7 > 0 ve R = 8 > 0.

b) Ücretsiz üye ise q indirgenmiş denklem (1)
olumsuz (q < 0)), o zaman denklemin farklı işaretli iki kökü vardır ve mutlak değerdeki daha büyük kök, eğer varsa pozitif olacaktır. R< 0 veya negatif ise p > 0.

Örneğin,

x2 + 4x - 5 = 0; x1 \u003d - 5 ve x2 \u003d 1, çünkü q = - 5 < 0 и R= 4 > 0;

x2 - 8x - 9 = 0; x1 = 9 ve x2= - 1 çünkü q = - 9 < и R= - 8 < 0.

5. Denklemlerin "transfer" yöntemiyle çözümü

İkinci dereceden denklemi düşünün eksen2 + içinde+ c = 0, nerede bir ≠ 0. Her iki parçasını da çarpmak a, denklemi elde ederiz a2x2 +abx+ ac= 0.

İzin vermek ah = y nerede X=; sonra denkleme geliyoruz

y2+ ile+ ac = 0,

buna eşdeğer. kökleri y1 ve y2 Vieta teoremi yardımıyla bulun. sonunda anladık x1= https://pandia.ru/text/78/082/images/image012_77.gif" width="24" height="43">.

Bu yöntemle katsayı a serbest terimle çarpılır, sanki ona "atılmış" gibi, bu yüzden denir aktarım yöntemi. Bu yöntem, Vieta teoremini kullanarak bir denklemin köklerini bulmak kolay olduğunda ve en önemlisi, diskriminant tam bir kare olduğunda kullanılır.

1. 2x2 - 11x + 15 = 0 denklemini çözün.

Çözüm. 2 katsayısını serbest terime "aktaralım", sonuç olarak denklemi elde ederiz.

y2 - 11 de+ 30 = 0.

Vieta teoremine göre, y1 = 5, y2 = 6, dolayısıyla x1 = https://pandia.ru/text/78/082/images/image014_69.gif" width="16 height=41" height="41" >, t e.

x1 = 2,5 x2 = 3.

Cevap: 2,5; 3.

6. Karenin katsayılarının özellikleridenklemler

A. İkinci dereceden bir denklem verilsin

ax2 + + c'de= 0, nerede a ≠ 0.

1. Eğer bir + + ile= 0 (yani, denklemin katsayılarının toplamı sıfıra eşittir), sonra x1 = 1, x2 = .

2. a - b + c ise= 0, veyab = a + c, sonra x1 = - 1, X 2 = - https://pandia.ru/text/78/082/images/image016_58.gif" width="44 height=41" height="41">.

Cevap: 1; 184">

Aşağıdaki durumlar mümkündür:

Düz bir çizgi ve bir parabol iki noktada kesişebilir, kesişme noktalarının apsisleri ikinci dereceden bir denklemin kökleridir;

Düz bir çizgi ve bir parabol birbirine değebilir (sadece bir ortak nokta), yani denklemin bir çözümü vardır;

Düz çizgi ve parabolün ortak noktaları yoktur, yani ikinci dereceden denklemin kökleri yoktur.

Örnekler

1. x2 - 3x - 4 = 0 denklemini grafiksel olarak çözelim (Şekil 2).

Çözüm. Denklemi formda yazıyoruz x2 = 3x + 4.

Bir parabol oluşturalım y = x2 ve doğrudan y= 3x + 4. Doğrudan de= 3x + 4, M(0; 4) ve N(3; 13) iki noktasından oluşturulabilir. Bir doğru ve bir parabol iki noktada kesişir A'dan B'ye apsisli x1= - 1 ve x2 = 4.

Cevap: x1= - 1, x, = 4.

8. İkinci dereceden denklemleri pusula ve cetvelle çözme

İkinci dereceden bir denklemin köklerini bulmak için aşağıdaki yöntemi öneriyoruz.

ah2+ içinde+ İle birlikte= 0

pusula ve cetvel kullanarak (Şek.).

Diyelim ki istenilen daire apsis eksenini noktalarda kesiyor. B(x1; 0) ve D(x2 ; 0) nerede x1 ve x2- denklemin kökleri eksen2 + içinde+İle birlikte=0,
ve y ekseni üzerindeki A(0; 1) ve C(0; ) noktalarından geçer..gif" width="197" height="123">

Yani: 1) noktalar oluşturun https://pandia.ru/text/78/082/images/image023_40.gif" width="171" height="45"> daire OX eksenini B(x1;0) noktasında kesiyor ) ve D(x1 ; 0) burada x1 ve x2 - ax2+bx+c ikinci dereceden denklemin kökleri = 0.

2) Dairenin yarıçapı, merkezin ordinatına eşittir , daire x eksenine B(x1; 0) noktasında dokunur, burada xx ikinci dereceden denklemin köküdür.

3) Dairenin yarıçapı, sol merkezin ordinatından küçük">

https://pandia.ru/text/78/082/images/image029_34.gif" width="612" height="372">40" height="14">

https://pandia.ru/text/78/082/images/image031_28.gif" width="612" height="432 src=">

Değiştirmelerden sonra nereden ve

basitleştirmeler, z2+pz+q=0 denklemi izler ve z harfi eğrisel ölçeğin herhangi bir noktasının etiketi anlamına gelir.

10. İkinci dereceden denklemleri çözmek için geometrik yöntem

Ve dört ekli kare, yani S=x2+10x+25. x2+10x'i 39 ile değiştirirsek, S = 39 + 25 = 64 elde ederiz, bu da karenin kenarının olduğu anlamına gelir. ABCD, yani segment AB= 8. Gerekli taraf için X elde ettiğimiz orijinal kare

Çözüm

Hepimiz okuldan mezuniyete kadar ikinci dereceden denklemlerin nasıl çözüleceğini biliyoruz. Ancak okul matematik dersinde, herhangi bir ikinci dereceden denklemin çözülebileceği, ikinci dereceden denklemlerin köklerinin formülleri incelenir. Ancak, bu konuyu daha derinlemesine inceledikten sonra, birçok denklemi çok hızlı ve rasyonel bir şekilde çözmenize izin veren ikinci dereceden denklemleri çözmenin başka yolları olduğuna ikna oldum.

Belki matematik orada başka boyutlarda bir yerdedir, gözle görülemez - her şey yazılıdır ve tüm yeni gerçekleri dünyalarla birlikte delikten alırız? ... Tanrı bilir; ancak fizikçiler, kimyagerler, ekonomistler veya arkeologlar dünyanın yapısının yeni bir modeline ihtiyaç duyarlarsa, bu model her zaman matematikçilerin üç yüz yıl önce koyduğu raftan alınabilir veya aynı yüzeyde yatan parçalardan birleştirilebilir. raf. Belki de bu parçaların bükülmesi, birbirine ayarlanması, parlatılması, hızlı bir şekilde birkaç yeni teorem burcunun işlenmesi gerekecek; ancak sonucun teorisi sadece ortaya çıkan fiili durumu açıklamakla kalmayacak, aynı zamanda sonuçları da tahmin edecektir! ...

Garip bir şey, her zaman haklı olan bu akıl oyunudur ...

Edebiyat

1. Alimov SHA., İlyin VA. ve diğerleri Cebir, 6-8. Lise 6-8 sınıfları için deneme kitabı. - M., Eğitim, 1981.

Lise için 2.Bradis matematik tabloları. Ed. 57. - M., Eğitim, 1990. S. 83.

3. Zlotsky - matematik öğretiminde görevler. Öğretmen için kitap. - M., Eğitim, 1992.

4.M., Matematik ("Birinci Eylül" gazetesinin eki), No. 21/96, 10/97, 24/97, 18/98, 21/98.

5. Okunev fonksiyonları, denklemler ve eşitsizlikler. Öğretmen için bir rehber. - M., Eğitim, 1972.

6. Solomnik B.C., Matematikte tatlı sorular ve problemler. Ed. 4, ekleyin. - M., Yüksek Okul, 1973.

7.M., Matematik ("Birinci Eylül" gazetesine ek), Sayı 40, 2000.

Gözden geçirmek

MOU "Sergievskaya ortaokulunun 11. sınıfındaki bir öğrencinin çalışması için

Kapsamlı okul"

1. YÖNTEM : Denklemin sol tarafının çarpanlara ayrılması.

denklemi çözelim

x 2 + 10x - 24 = 0.

Sol tarafı çarpanlarına ayıralım:

x 2 + 10x - 24 \u003d x 2 + 12x - 2x - 24 \u003d x (x + 12) - 2 (x + 12) \u003d (x + 12) (x - 2).

Bu nedenle, denklem şu şekilde yeniden yazılabilir:

(x + 12)(x - 2) = 0

2. YÖNTEM : Tam kare seçim yöntemi.

denklemi çözelim x 2 + 6x - 7 = 0.

Sol tarafta tam bir kare seçelim.

Bunu yapmak için x 2 + 6x ifadesini aşağıdaki biçimde yazıyoruz:

x 2 + 6x = x 2 + 2 x 3.

Ortaya çıkan ifadede, ilk terim x sayısının karesidir ve ikincisi x'in 3'ün çift çarpımıdır. Bu nedenle, tam kareyi elde etmek için 3 2 eklemeniz gerekir, çünkü

x 2+ 2 x 3 + 3 2 \u003d (x + 3) 2.

Şimdi denklemin sol tarafını dönüştürüyoruz

x 2 + 6x - 7 = 0,

ekleme ve çıkarma 3 2 . Sahibiz:

x 2 + 6x - 7 = x 2+ 2 x 3 + 3 2 - 3 2 - 7 = (x + 3) 2 - 9 - 7 = (x + 3) 2 - 16.

Böylece, bu denklem aşağıdaki gibi yazılabilir:

(x + 3) 2 - 16 = 0, (x + 3) 2 = 16.

Sonuç olarak, x + 3 - 4 = 0, x 1 = 1 veya x + 3 = -4, x 2 = -7.

3. YÖNTEM :İkinci dereceden denklemlerin formülle çözümü.

Denklemin her iki tarafını da çarpın

2+bx + c = 0, a ≠ 0

4a'da ve art arda elimizde:

4a 2x2 + 4abx + 4ac = 0,

((2ax) 2 + 2axb + b 2 ) - b 2 + 4 AC = 0,

(2ax + b) 2 = b 2 - 4ac,

2ax + b \u003d ± √ b 2 - 4ac,

2ax \u003d - b ± √ b 2 - 4ac,

Örnekler.

a) Denklemi çözelim: 4x2 + 7x + 3 = 0.

bir = 4,b= 7, c = 3,D = b 2 - 4 AC = 7 2 - 4 4 3 = 49 - 48 = 1,

D > 0, iki farklı kök;

Böylece, pozitif bir ayrımcı durumunda, yani. de

b 2 - 4 AC >0 , denklem 2+bx + c = 0 iki farklı kökü vardır.

b) Denklemi çözelim: 4x 2 - 4x + 1 = 0,

bir = 4,b= - 4, c = 1,D = b 2 - 4 AC = (-4) 2 - 4 4 1= 16 - 16 = 0,

D = 0, bir kök;

Yani, eğer diskriminant sıfır ise, yani. b 2 - 4 AC = 0 , sonra denklem

2+bx + c = 0 tek bir kökü var

içinde) Denklemi çözelim: 2x 2 + 3x + 4 = 0,

bir = 2,b= 3, c = 4,D = b 2 - 4 AC = 3 2 - 4 2 4 = 9 - 32 = - 13 , D < 0.

Bu denklemin kökü yoktur.

Yani, eğer diskriminant negatif ise, yani. b 2 - 4 AC < 0 ,

denklem 2+bx + c = 0 kökleri yoktur.

İkinci dereceden denklemin köklerinin formülü (1) 2+bx + c = 0 kökleri bulmanızı sağlar hiç ikinci dereceden denklem (varsa), indirgenmiş ve eksik dahil. Formül (1) sözlü olarak şu şekilde ifade edilir: ikinci dereceden bir denklemin kökleri, payı, zıt işaretle alınan ikinci katsayıya eşit olan bir kesre eşittir, artı eksi bu katsayının karesinin karekökü, serbest terimle ilk katsayının ürününü dört katına çıkarmadan, ve payda birinci katsayının iki katıdır.

4. YÖNTEM: Vieta teoremini kullanarak denklemlerin çözümü.

Bilindiği gibi, verilen ikinci dereceden denklem forma sahiptir

x 2+piksel + c = 0. (1)

Kökleri Vieta teoremini tatmin eder; a=1 forma sahip

x 1 x 2 = q,

x 1 + x 2 = - p

Bundan aşağıdaki sonuçları çıkarabiliriz (köklerin işaretleri p ve q katsayılarından tahmin edilebilir).

a) Özet terim ise q indirgenmiş denklem (1) pozitiftir ( q > 0 ), o zaman denklemin aynı işaretin iki kökü vardır ve bu ikinci katsayının kıskançlığıdır. p. Eğer bir R< 0 , o zaman her iki kök de negatifse R< 0 , o zaman her iki kök de pozitiftir.

Örneğin,

x 2 – 3 x + 2 = 0; x 1 = 2 ve x 2 = 1, çünkü q = 2 > 0 ve p = - 3 < 0;

x 2 + 8 x + 7 = 0; x 1 = - 7 ve x 2 = - 1, çünkü q = 7 > 0 ve p= 8 > 0.

b) Ücretsiz üye ise q indirgenmiş denklem (1) negatiftir ( q < 0 ), o zaman denklemin farklı işaretli iki kökü vardır ve eğer mutlak değerdeki daha büyük kök pozitif olacaktır: p < 0 veya olumsuz ise p > 0 .

Örneğin,

x 2 + 4 x – 5 = 0; x 1 = - 5 ve x 2 = 1, çünkü q= - 5 < 0 ve p = 4 > 0;

x 2 – 8 x – 9 = 0; x 1 = 9 ve x 2 = - 1, çünkü q = - 9 < 0 ve p = - 8 < 0.

5. YÖNTEM: "Transfer" yöntemini kullanarak denklemleri çözme.

İkinci dereceden denklemi düşünün

2+bx + c = 0, nerede bir ≠ 0.

Her iki parçasını da a ile çarparak denklemi elde ederiz.

2x2 + birbx + ac = 0.

İzin vermek ah = y, nerede x = y/a; sonra denkleme geliyoruz

2+ile+ ac = 0,

buna eşdeğer. kökleri 1 ve de 2, Vieta teoremi kullanılarak bulunabilir.

sonunda anladık

x 1 \u003d y 1 / bir ve x 1 \u003d y 2 / bir.

Örnek.

denklemi çözelim 2x 2 - 11x + 15 = 0.

Çözüm. 2 katsayısını serbest terime "aktaralım", sonuç olarak denklemi elde ederiz.

y 2 - 11y + 30 = 0.

Vieta teoremine göre

y 1 = 5 x 1 = 5/2x 1 = 2,5

y2 = 6x 2 = 6/2 x 2 = 3.

Cevap: 2.5; 3.

6. YÖNTEM: İkinci dereceden bir denklemin katsayılarının özellikleri.

ANCAK. ikinci dereceden denklem olsun

2+bx + c = 0, nerede bir ≠ 0.

1) Eğer, bir+b+ c \u003d 0 (yani katsayıların toplamı sıfırdır), sonra x 1 \u003d 1,

x 2 \u003d s / bir.

Kanıt. Denklemin her iki tarafını da ≠ 0'a bölersek, indirgenmiş ikinci dereceden denklemi elde ederiz.

x 2 + b/ a x + c/ a = 0.

Vieta teoremine göre

x 1 + x 2 = - b/ a,

x 1 x 2 = 1 c/ a.

koşula göre a -b+ c = 0, nerede b= a + c. Böylece,

x 1 + x 2 = -a+ b / a \u003d -1 - c / a,

x 1 x 2 \u003d - 1 (- c / a),

şunlar. x 1 = -1 ve x 2 =c/ a, ki kanıtlamamız gerekiyordu.

Örnekler

1) Denklemi çözün 345x 2 - 137x - 208 = 0.

Çözüm.Çünkü bir +b+ c \u003d 0 (345 - 137 - 208 \u003d 0), sonra

x 1 = 1, x 2 =c/ a = -208/345.

Cevap 1; -208/345.

2) Denklemi çözün 132x 2 - 247x + 115 = 0.

Çözüm.Çünkü bir +b+ c \u003d 0 (132 - 247 + 115 \u003d 0), sonra

x 1 = 1, x 2 =c/ a = 115/132.

Cevap 1; 115/132.

B. ikinci katsayı ise b = 2 k bir çift sayı, o zaman köklerin formülü

Örnek.

denklemi çözelim 3x2 - 14x + 16 = 0.

Çözüm. Sahibiz: bir = 3,b= - 14, c = 16,k = - 7 ;

D = k 2 – AC = (- 7) 2 – 3 16 = 49 – 48 = 1, D > 0, iki farklı kök;