Trabaho ng pananaliksik na "10 paraan upang malutas ang mga quadratic equation". Mga paraan upang malutas ang mga quadratic equation 10 paraan upang malutas ang square

Kagawaran ng Edukasyon at Agham

Rehiyon ng Kemerovo

GOU SPO "Mariinsky Agricultural College"

10 PARAAN SA SOLUSYON

MGA EQUATIONS NG PAPARTAS

ax ²+in+c=0

Nakumpleto ang gawain:

Haring Pananampalataya,

pangkat na mag-aaral 161

specialty 260807 "Teknolohiya ng mga produktong catering"

Superbisor:

Matveeva Olga Vasilievna,

guro sa matematika

Mariinsk, 2013

I. Panimula

II. Kasaysayan ng pangyayari quadratic equation

2. Quadratic equation sa sinaunang Babylon.

3. Quadratic equation sa EuropeXIII – XVII mga siglo

III. Mga paraan upang malutas ang mga quadratic equation

3. Mga partikular na kaso ng paglutas ng mga quadratic equation:

a) koepisyent a - napakaliit,

b) koepisyent kasama - napakaliit.

4. Solusyon ng mga equation gamit ang Vieta theorem.

6. Solusyon ng mga equation sa pamamagitan ng paraan ng "transfer".

9. Paglutas ng mga quadratic equation gamit ang isang nomogram.

IV. Konklusyon

V. Panitikan

I. PANIMULA

« Kadalasan ay mas kapaki-pakinabang para sa isang mag-aaral ng algebra na lutasin ang parehong problema sa tatlong magkakaibang paraan kaysa sa paglutas ng tatlo o apat na magkakaibang problema. Sa pamamagitan ng paglutas ng isang problema sa iba't ibang mga pamamaraan, posible na malaman sa pamamagitan ng paghahambing kung alin ang mas maikli at mas mahusay. Ganyan ginagawa ang karanasan."

W. Sawyer

Ang mga quadratic equation ay ang pundasyon kung saan nakasalalay ang maringal na edipisyo ng algebra. Ang mga quadratic equation ay malawakang ginagamit sa paglutas ng iba't-ibangtrigonometric, exponential, logarithmic, irrational, transendental equation at inequalities, isang malaking bilang iba't ibang uri mga gawain.

Ang teorya ng mga equation ay sumasakop sa isang nangungunang lugar sa algebra at matematika sa pangkalahatan. Ang lakas ng teorya ng mga equation ay hindi lamang ito ay may teoretikal na kahalagahan para sa kaalaman ng mga likas na batas, ngunit nagsisilbi rin sa mga praktikal na layunin. Karamihan sa mga problema sa buhay ay napupunta sa paglutas iba't ibang uri mga equation, at mas madalas ang mga ito ay mga equation ng isang quadratic form.

Ang quadratic equation ay isang malaki at mahalagang klase ng mga equation na maaaring lutasin gamit ang parehong mga formula at elementary functions.

AT kurso sa paaralan matematika, nakikilala natin ang ilang uri ng quadratic equation, at ginagawa ang solusyon gamit ang mga karaniwang formula. Kasabay nito, ang modernong siyentipiko at metodolohikal na pananaliksik ay nagpapakita na ang paggamit ng iba't ibang mga pamamaraan at pamamaraan ay maaaring makabuluhang mapabuti ang kahusayan at kalidad ng pag-aaral ng mga solusyon sa quadratic equation.

Kaya, may pangangailangang pag-aralan ang iba't ibang paraan ng paglutas ng mga quadratic equation.

Ang lahat ng nasa itaas ay tumutukoykaugnayan mga paksa ng pananaliksik.

Problema Ang pananaliksik ay upang isaalang-alang ang iba't ibang, kabilang ang mga hindi karaniwang paraan ng paglutas ng mga quadratic equation.

Target ang trabaho ay ang pag-aaral mga teoretikal na pundasyon at ang kanilang aplikasyon sa paglutas ng mga quadratic equation.

Bagay pananaliksik: quadratic equation at ang kanilang mga solusyon.

Mga gawain:

Magsagawa ng pagsusuri ng panitikan sa paksang ito.

Upang pag-aralan ang kasaysayan ng pagbuo ng mga quadratic equation.

Upang pag-aralan ang iba't ibang paraan ng paglutas ng mga quadratic equation, kabilang ang mga hindi pamantayan, at upang subukan ang materyal sa pagsasanay.

II. KASAYSAYAN NG PINAGMULAN NG QUADRATIC EQUATIONS

1. Quadratic equation sa India.

Ang mga problema para sa quadratic equation ay matatagpuan sa astronomical tractor na "Aryabhattiam", na pinagsama-sama noong 499 ng Indian mathematician at astronomer na si Aryabhata. Isa pang iskolar ng India - Brahmagupta (VIIc.) binalangkas pangkalahatang tuntunin mga solusyon ng quadratic equation. Ang panuntunan ng Brahmagupta ay mahalagang tumutugma sa modernong isa.

Sa sinaunang India, ang mga pampublikong kumpetisyon sa paglutas ng mahihirap na problema ay karaniwan. Sa isa sa mga lumang aklat ng India, ang mga sumusunod ay sinabi tungkol sa gayong mga kumpetisyon: “Kung paanong ang araw ay nanggagaling sa mga bituin sa kanyang ningning, gayon din taong siyentipiko lampasan ang kaluwalhatian ng iba sa mga pampublikong pagpupulong, pagmumungkahi at paglutas ng mga problema sa algebra. Ang mga gawain ay kadalasang binibihisan sa anyong patula.

Narito ang isa sa mga problema ng sikat na Indian mathematicianXII sa Bhaskara.

Makulit na kawan ng mga unggoy

Pagkakain ng kapangyarihan, nagsaya.

Pinagsama-sama nila ang walong bahagi

Nagsasaya sa parang

At labindalawa sa pamamagitan ng baging

Nagsimula silang tumalon, nakabitin..

Ang daming unggoy

Sabihin mo sa akin, sa kawan na ito?

Ang solusyon ni Bhaskara ay nagpapahiwatig na alam niya ang tungkol sa dalawang pagpapahalaga ng mga ugat ng quadratic equation.

x 2 - 64 = - 768,

x 2 - 64x +32 2 \u003d - 768 + 1024,

(x - 32) 2 \u003d 256,

x 1 = 16, x 2 = 48

2. Mga Quadratic Equation sa Sinaunang Babylon.

Alam ng mga Babylonians kung paano lutasin ang mga quadratic equation noong 2000 BC. Paglalapat ng moderno algebraic notation, maaari nating sabihin na sa kanilang mga tekstong cuneiform ay mayroong, bilang karagdagan sa mga hindi kumpleto, tulad, halimbawa, mga kumpletong equation.

Ang tuntunin para sa paglutas ng mga equation na ito, na nakasaad sa mga tekstong Babylonian, ay talagang kasabay ng modernong isa, ngunit hindi alam kung paano napunta ang mga Babylonians sa panuntunang ito. Halos lahat ng mga tekstong cuneiform na natagpuan sa ngayon ay nagbibigay lamang ng mga problema sa mga solusyon na nakasaad sa anyo ng mga recipe, nang walang mga tagubilin kung paano

sila ay natagpuan. Kahit na mataas na lebel pag-unlad ng algebra sa Babylon, sa mga tekstong cuneiform ay walang konsepto ng negatibong numero at pangkalahatang pamamaraan para sa paglutas ng mga quadratic equation.

3. Quadratic equation sa Europe noong XII – XVII mga siglo

Ang mga form para sa paglutas ng mga quadratic equation sa modelo ng al-Khwarizmi sa Europe ay unang inilarawan sa "Book of Abah", na isinulat noong 1202 ng Italian mathematician na si Leonardo Fibonacci. Ang may-akda ay nakapag-iisa na bumuo ng ilang bago mga halimbawa ng algebraic paglutas ng problema at siya ang una sa Europa na lumapit sa pagpapakilala ng mga negatibong numero. Ang kanyang libro ay nag-ambag sa paglaganap ng algebraic na kaalaman hindi lamang sa Italya, kundi pati na rin sa Alemanya, Pransya at iba pang mga bansa sa Europa. Maraming mga gawain mula sa "Aklat ni Abah" ang inilipat sa halos lahat ng mga aklat-aralin sa EuropaXVI – XVII mga siglo at bahagyang XVIII sa.

Pangkalahatang tuntunin para sa paglutas ng mga quadratic na equation ay binawasan sa isang solong canonical formX 2 + bx = kasama kasama ang lahat ng posibleng kumbinasyon ng mga palatandaan at koepisyentb , c , ay binuo sa Europa noong 1544 ni M. Stiefel. Derivation ng formula para sa paglutas ng isang quadratic equation sa pangkalahatang pananaw Ang Viet ay, ngunit ang Viet ay nakilala lamang ang mga positibong pinagmulan ng Viet, ang sikat na Pranses na siyentipiko, na isang abogado din sa pamamagitan ng propesyon. Ang mga siyentipikong Italyano na sina Tartaglia, Cardano, Bombelli ay kabilang sa mga unang inXVIsa. Isaalang-alang, bilang karagdagan sa positibo, at negatibong mga ugat. Lamang saXVIIsa. Salamat sa mga gawa ni Girrard, Descartes, Newton at iba pang mga siyentipiko, ang paraan ng paglutas ng mga quadratic equation ay tumatagal sa isang modernong hitsura.

III. IBA'T IBANG PARAAN NG PAGSOLBA NG QUADRATIC EQUATIONS

1. Pangkalahatang view ng quadratic equation at mga karaniwang formula para sa solusyon nito.

Equation ng form na palakol 2 + in + c = 0 (1) , kung saan ang a, b, c - ilang mga numero, ata ≠ 0, tinatawag na parisukat.

Ang isang quadratic equation ay tinatawag ding equation ng pangalawang degree.

Sa equation (1) a unang tinawag koepisyent, sa- pangalawa koepisyent, kasama - ang ikatlong koepisyent o libreng miyembro.

Pagpapahayag ng anyo D = sa 2 – 4ac ay tinatawag na discriminant (distinguisher) ng quadratic equation.

Alalahanin na ang ugat (o solusyon) ng isang equation na may hindi alamX ang numero ay tinatawag, kapag pinapalitan sa equation sa halip naX ang isang tamang numerical equation ay nakuha.

Upang malutas ang isang equation ay nangangahulugang hanapin ang lahat ng mga ugat nito o ipakita na wala.

Ang pagkakaroon ng mga ugat ng quadratic equation (1) ay depende sa tanda ng discriminantD, kaya ang solusyon ng equation ay dapat magsimula sa pagkalkulaDupang malaman kung ang quadratic equation (1) ay may mga ugat, at kung gayon, ilan.

Tatlong kaso ang posible:

Kung ang D>0, pagkatapos ang quadratic equation (1) ay may dalawang magkaibang tunay na ugat:

sa 2 - 4ac.

Kung ang D<0, то квадратное уравнение не имеет действительных корней.

Ipagpalagay na sa ilang equation ginawa namin ang sumusunod na pagbabagong-anyo: binuksan namin ang mga bracket, kung mayroon man, sinira ang mga denominator kung ang equation ay may mga fractional na termino, inilipat ang lahat ng mga termino sa kaliwang bahagi ng equation at gumawa ng pagbawas ng mga katulad na termino. Kung pagkatapos noon ay may terminong naglalaman ng hindi kilalang parisukat sa kaliwang bahagi ng equation, at walang mga terminong naglalaman ng hindi alam sa mas mataas na antas, kung gayon ang isang parisukat na equation ay nakuha. Ang pangkalahatang anyo ng naturang equation ay 2 + bx + c = 0.

Tandaan na ang coefficienta maaari tayong palaging maging positibo, pagbabago, kung kinakailangan, bago ang lahat ng mga tuntunin ng equation ang mga palatandaan sa kabaligtaran.

Halimbawa 1

Maghanap ng mga logroa, sa at kasama para sa equation:
.

Desisyon:

Pagpapalawak ng mga bracket:
,

Pagsira sa denominator: 72 + 2x 2 = 15x 2 + 15x,

Inilipat namin ang lahat ng miyembro sa kaliwang bahagi at ginagawa ang cast: - 13x 2 - 15x + 72 = 0,

Mga palatandaan ng pagbabago: 13x 2 + 15x - 72 = 0,

Odds a, b , at kasama kinuha ng pangkalahatang anyo ng quadratic equation sa halimbawang ito ang mga sumusunod na partikular na halaga:a = 13, b = 15 at c = - 72 .

Halimbawa 2

Lutasin ang equation:

Solusyon: >0, dalawang ugat;

Sagot: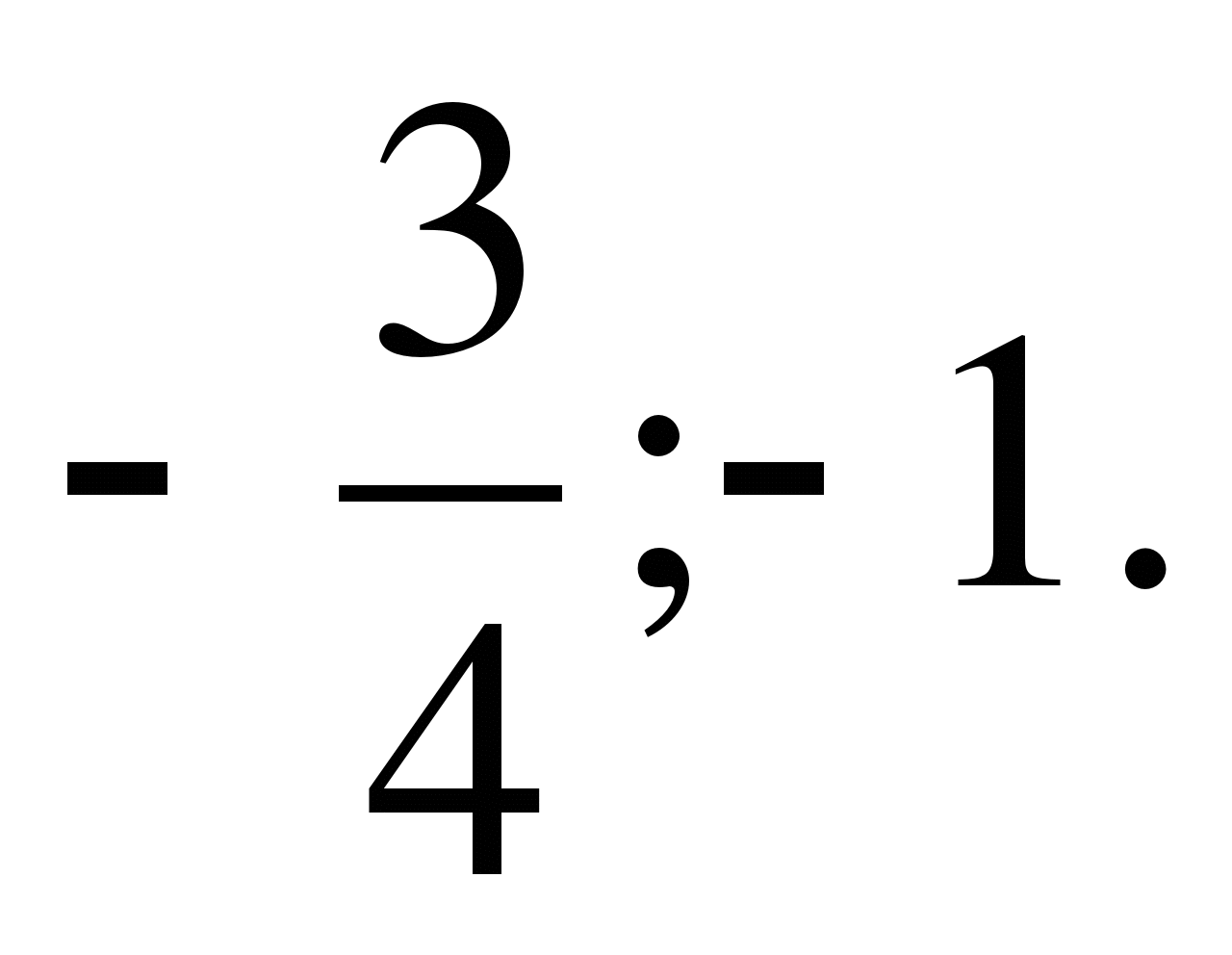

Halimbawa 3

Lutasin ang equation:

Desisyon: D =0, isang ugat;

Sagot:

Halimbawa 4

Lutasin ang equation:

Desisyon:<0.

Ang equation ay walang tunay na ugat.

Sagot: Walang tunay na ugat.

Kung isasaalang-alang ang solusyon ng mga quadratic equation, makikita natin na ang mga equation na ito ay minsan ay may dalawang ugat, minsan isa, minsan wala. Gayunpaman, sumang-ayon silang ipatungkol sa mga quadratic equation sa lahat ng kasodalawang ugat , hindi sinasabi na ang mga ugat ay maaaring minsan ay pantay, minsan ay haka-haka. Ang dahilan para sa naturang kasunduan ay ang mga pormula na nagpapahayag ng mga haka-haka na ugat ng isang equation ay may parehong mga katangian na nabibilang sa tunay na mga ugat, ito ay binubuo lamang sa pagsasagawa ng mga operasyon sa mga haka-haka na dami, na ginagabayan ng mga patakaran na nagmula para sa mga tunay na dami, habang tinatanggap iyon (
) 2 = - a. Katulad nito, kapag ang isang equation ay may isang ugat, magagawa natin, sa pamamagitan ng pagsasaalang-alang sa ugat na ito bilangdalawang magkapareho, katangian sa kanila ang parehong mga katangian na nabibilang sa iba't ibang mga ugat ng equation. Ang pinakasimple sa mga katangiang ito ay ipinahayag sa sumusunod na teorama.

Teorama: Ang kabuuan ng mga ugat ng isang quadratic equation, kung saan ang coefficient ng hindi alam sa 2nd degree ay 1, ay katumbas ng coefficient ng hindi alam sa unang degree, na kinuha gamit ang kabaligtaran na sign; ang produkto ng mga ugat ng equation na ito ay katumbas ng libreng termino.

Patunay: Tinutukoy ng α at β ang mga ugat ng equationX 2 +px+ q = 0 , magkakaroon tayo (anuman ang mga ugat na ito)

Ang produktong ito ay matatagpuan sa isang pinaikling paraan, batay sa pagkakapantay-pantay (a + b)(a – b) = a 2 – b 2 :

Kung ang α at β ay mga ugat ng equationOh 2 + bx + c = 0 , o ano ang parehong equation

, pagkatapos ay magkakaroon ito

.

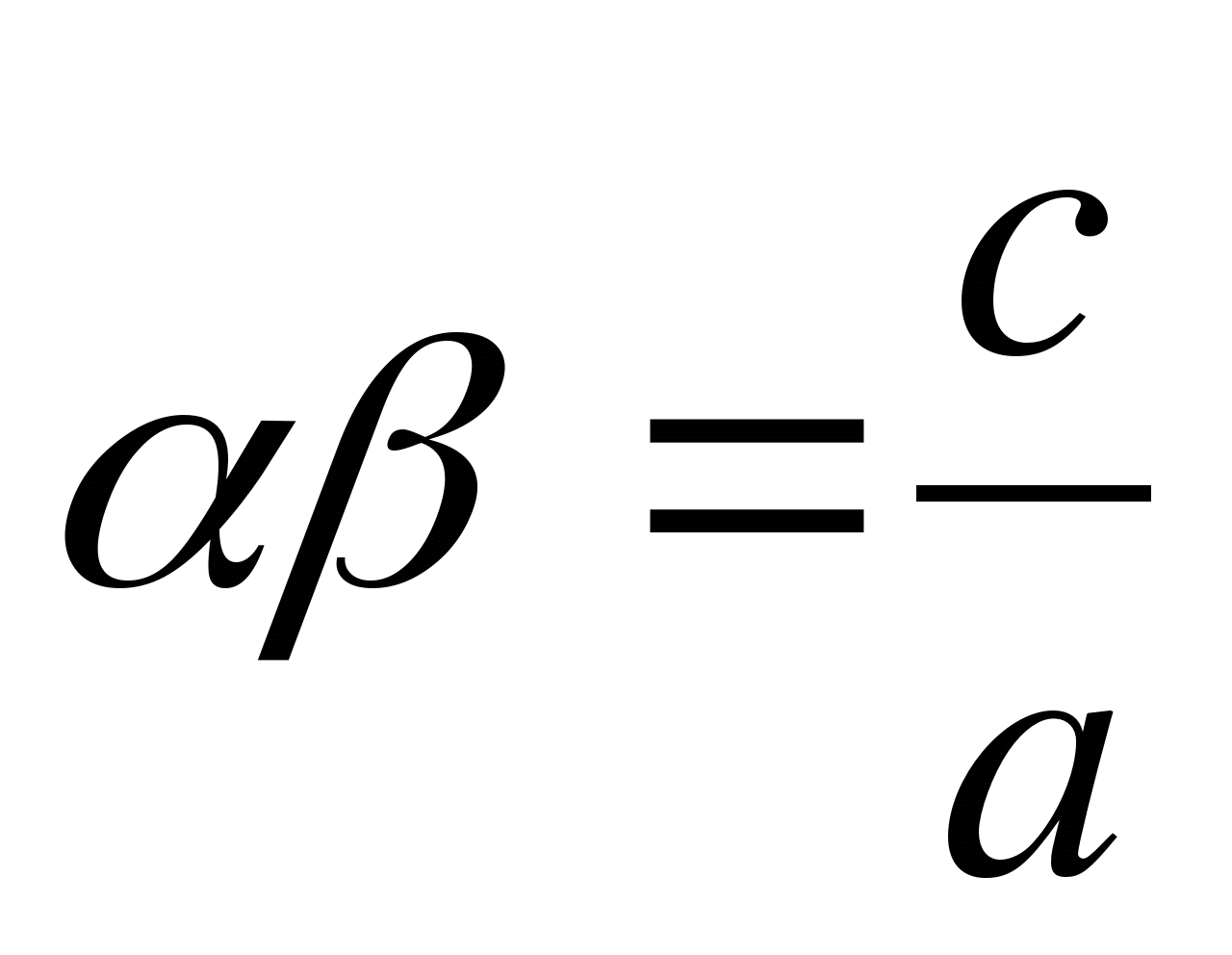Inverse theorem: Kung dami α, β, p at q ay ganyan α + β = - R at αβ = q , pagkatapos β at α ay ang mga ugat ng equationX 2 +px+ q = 0 .

Patunay: Ito ay kinakailangan upang patunayan na ang bawat isa sa mga damiβ at α natutugunan ang equationX 2 +px+ q = 0 . Mula sa pagkakapantay-pantay α + β = - p at α \u003d -p - β , pagkatapos kung saan ang pagkakapantay-pantayαβ = q nagbibigay

o
.

Ibig sabihin, β ay ang ugat ng equationOh 2 + bx + c = 0 ; sa parehong paraan, maaari naming i-verify iyonα ay ang ugat ng parehong equation.

1st consequence. Ang mga ugat na ito ay maaaring gamitin upang bumuo ng isang quadratic equation. Hayaang kailanganin na bumuo ng isang equation na ang mga ugat ay magiging 2 at - 3. Ipagpalagay na 2 + (- 3) \u003d - p at 2 (- 3) \u003dq, nakita namin - p \u003d 1, q= - 6. Kaya, ang nais na equation ay

X 2 + x - 6 = 0

Katulad nito, nakita natin na - 2 at - 2 ang mga ugat ng equation x 2 + 4x + 4 = 0, 3 at 0 ang mga ugat ng equation na x 2 - 3x = 0, atbp.

2nd corollary. Nang walang paglutas ng isang quadratic equation, matutukoy ng isa ang mga palatandaan ng mga ugat nito kung ang mga ugat na ito ay totoo. Hayaan, halimbawa, mayroon tayong equation x 2 + 8x +10 = 0. Dahil sa halimbawang ito ang numero
- qay isang positibong numero, kung gayon ang parehong mga ugat ay dapat na totoo. Alamin natin, nang hindi nilulutas ang mga equation, ang mga palatandaan ng mga ugat na ito. Upang gawin ito, pinagtatalunan namin ang mga sumusunod: pagbibigay-pansin muna sa libreng termino (+ 10), nakita namin na mayroon itong + sign; kaya ang produkto ng mga ugat ay dapat napositibo , ibig sabihin, ang parehong mga ugat ay maypareho palatandaan. Upang matukoy kung alin, bigyang-pansin natin ang koepisyent saX (i.e. sa +8) mayroon itong + sign; samakatuwid, ang kabuuan ng mga coefficientnegatibo ; dahil ang parehong mga palatandaan sa mga ugat ay dapat naminus .

Ang katulad na pangangatwiran ay maaaring matukoy ang mga palatandaan sa mga ugat sa anumang iba pang kaso. Kaya ang equation x 2 + 8x - 10 = 0 ay may mga ugat na may iba't ibang palatandaan

(dahil ang kanilang produkto ay negatibo), at ang negatibong ugat ay may malaking ganap na halaga (dahil ang kanilang kabuuan ay negatibo); equation x 2 - 8 - 10 \u003d Ang 0 ay mayroon ding mga ugat na may iba't ibang mga palatandaan, ngunit ang isang malaking ganap na halaga ay kabilang sa isang positibong ugat.

2. Solusyon ng mga hindi kumpletong quadratic equation.

Ang isang quadratic equation ay tinatawag na hindi kumpleto kapag hindi ito naglalaman ng terminong naglalamanX , o walang libreng termino. Ang mga hindi kumpletong quadratic equation ay maaari lamang sa sumusunod na tatlong uri:

a) palakol 2 + c = 0; b) palakol 2 + bx= 0; kasama) palakol 2 = 0.

Tingnan natin ang bawat solusyon.

a) Mula sa equation X 2 + c = 0 nahanap

Oh 2 = - c at x 2 = .

Ang pagkakapantay-pantay na ito ay nangangailangan na ang parisukat ng hindi alam ay katumbas ng numero ; kaya ang hindi alam ay dapat na katumbas ng parisukat na ugat ng dami na iyon. Ito ay posible lamang kapag ang dami ay isang positibong numero, ano ang mangyayari kapagkasama at a may magkasalungat na mga palatandaan (kung, halimbawa,kasama = - 8, a = + 2, pagkatapos

Ipahiwatig natin sa pamamagitan ng tanda tanging ang arithmetic value ng square root at isaalang-alang na ang square root ng isang positive number ay may dalawang value; pagkatapos, nagsasaad ng isang halaga sa pamamagitan ngX 1 , at ang isa sa pamamagitan ng X 2, maaari tayong magsulat

Kung mga numero kasama at a magkaroon ng parehong tanda, kung gayon ay isang negatibong numero; tapos yung equation ah 2 + c = 0 ay hindi masisiyahan ng anumang tunay na numero; sa kasong ito, ang equation ay sinasabing may dalawahaka-haka ugat.

Halimbawa 5

Lutasin ang equation:3x 2 – 27 = 0.

Solusyon: 3x 2 = 27; x 2 = 9; x =

Sagot: x =

Halimbawa 6

Lutasin ang equation:X 2 +25 = 0.

Solusyon: x 2 = - 25; x =
; haka-haka na mga ugat.

Sagot: x = + - 5 i.

b) Upang malutas ang equationOh 2 + bx = 0 , isipin natin na ganitoX( palakol + b ) = 0 . Ang produkto ay maaaring katumbas ng zero lamang kapag alinman sa mga salik sero; samakatuwid, ang equation na isinasaalang-alang ay nasiyahan kung ipagpalagay natin iyonx = 0 o ah + b = 0 /

Ang pangalawang pagkakapantay-pantay ay nagbibigay
Kaya ang equationOh 2 + bx = 0 may dalawang ugat

x 1 = 0 at

Halimbawa 7

Lutasin ang equation: 2x 2 - 7x = 0.

Solusyon: 2x 2 – 7x = 0, x(2x – 7) = 0; X 1=0; x 2 = .

Sagot: x 1 \u003d 0; x 2 = .

sa) Panghuli, ang quadratic equationpalakol 2 = 0 ay malinaw na mayroon lamang isang solusyon x = 0.

3. Mga partikular na kaso ng quadratic equation.

a) Ang kaso kapag ang koepisyenta napakaliit.

Pagkalkula ng mga ugat ng equation ax 2 + bx + c= 0 ayon sa pangkalahatang formula na nagmula sa itaas, ito ay mahirap sa kasong ito, kapag ang koepisyenta napakaliit na bilang kumpara sab at kasama . Sa katunayan, sa pamamagitan ng pagkalkula ng mga ugat sa pamamagitan ng formula

Sa karamihan ng mga kaso, dapat tayong maging kontento sa tinatayang halaga
, at samakatuwid ang buong numerator. Sa pamamagitan ng paghahati sa tinatayang halaga na ito sa pamamagitan ng 2a, sa gayon ay hinahati natin sa 2a at ang error kung saan kinakalkula ang numerator ng formula. Ngunit dahil, ayon sa panukala, ang 2a ay isang napakaliit na bahagi, ang paghahati sa isang maliit na bahagi ay katumbas ng pagpaparami ng mas malaking bilang, ang error ay tumataas nang malaki, bilang isang resulta kung saan ang huling resulta ay malayo sa tunay na isa. Kung, halimbawa, 2a = 0.0001 at kinakalkula namin
hanggang sa ikaapat na decimal place, ang margin ng error sa huling resulta ay magiging 0.0001: 0.00001 = 10.

Upang makalkula ang mga ugat ng equation sa kasong ito, isang mas maginhawang paraan ng tinatawag nasunud-sunod na approximation.

Tandaan na para sa isang napakaliit na halagaa ang isa sa mga ugat ng equation ay bahagyang naiiba sa , at ang isa ay napakalaking bilang (sa ganap na halaga). Sa katunayan, ang equation 2 + bx + c= 0 ay katumbas ng equation

,

na maaaring bigyan ng hitsura

bilang - a malapit sa zero, kung gayon ang huling equation ay maaaring masiyahan ng mga naturang halagaX , kung saan ang isa sa mga salik sa kaliwang bahagi ng equation ay lumalabas na napakaliit na numero, at ang isa ay hindi masyadong malaki; magaganap ito o kapag nagbigay tayoX isang napakalaking ganap na halaga, o kung kailanX magiging malapit sa .

Ipakita natin kung paano kalkulahin ang isa sa mga ugat, na hindi gaanong naiiba

(nakahanap tayo ng isa pang ugat sa pamamagitan ng pagbabawas ng una sa ).

Mula sa equation na hinuhusgahan natin
.

Bilang a napakaliit na bilang atX at b hindi masyadong malaki at hindi masyadong maliit, pagkatapos ay ang ganap na halaga ng fraction
napakaliit. Ang pagpapabaya sa terminong ito, nakukuha natinx unang pagtataya

Ang pagpasok ng halagang ito sa kanang bahagi ng equation (1), nakukuha natinpangalawang pagtataya, mas tumpak kaysa sa una:

Ang pagpasok ng dami na ito sa unang bahagi ng equation (1), makuha natinikatlong pagtatantya , mas tumpak. Sa katulad na paraan, maaari nating makuha, kung kinakailangan, ang pang-apat at susunod na pagtatantya.

Halimbawa 8

Lutasin ang equation: 0.003x 2 + 5x - 2 = 0

Desisyon:
.

Unang pagtataya = 0.4. Ang numerong ito ay mas totoong halaga ng x 2 dahil kailangan naming itaponnegatibo miyembro - 0.0006x 2.

Pangalawang pagtatantya = 0.4 - 0.0006 (0.4) 2 = 0.399904. Ang numerong ito ay mas mababa sa totoong halagaX 2 bilang na mas malaki kaysa sa x 2 , na nagiging sanhi ng pagtaas ng subtrahend at pagbaba ng pagkakaiba.

Ang ikatlong pagtatantya ay magiging mas malaki kaysa sa tunay na halagaX , pang-apat na mas mababa, atbp.

Mula noong 0.4 > x > 0.399904, sa halip na kuninX isa sa mga pagtatantya na ito, gagawa kami ng error na mas mababa sa 0.4 - 0.399904, ibig sabihin, mas mababa sa 0.0001. Ang isa pang ugat ay nakuha sa pamamagitan ng pagbabawas ng natagpuang ugat mula sa
Kung kukunin natin ang numerong 0.4 para sa unang ugat, kung gayon ang isa ay 1667, (6).

b) Ang kaso kung kailan kasama isang napakaliit na bilang.

Ang sunud-sunod na paraan ng pagtatantya ay naaangkop din kapag ang libreng termino ng equation ay napakaliit na bilang kumpara saa at b . Sa kasong ito, ang isa sa mga ugat ay malapit sa
at ang isa ay napakaliit na halaga. Ito ay madaling i-verify kung ang equation ay ibinigay ang form

Dahil, ayon sa panukala, ang ganap na halaga aykasama ay napakaliit, kung gayon ang equation ay malinaw na masisiyahan kapagX , o napakalapit sa 0, o napakakaunting pagkakaiba sa

Upang makahanap ng ugat na may napakaliit na halaga, kinakatawan namin muli ang equation sa anyo

Bilang a at b ang kakanyahan ng mga numero ay hindi masyadong malaki at hindi masyadong maliit, ngunit ang ganap na halagaX 2 ay napakaliit, pagkatapos ay para sa unang pagtatantya maaari nating pabayaan ang termino
; pagkatapos makuha namin
.

Ang paglalagay ng halagang ito sa lugarX sa kanang bahagi ng equation (1), nakuha namin ang pangalawang approximation; gayundin, makikita natin, kung kinakailangan, ang mga sumusunod na pagtatantya.

4. Paglutas ng mga equation gamit ang Vieta theorem

(direkta at baligtad).

Ang ibinigay na quadratic equation ay may anyo

Ang mga ugat nito ay nagbibigay-kasiyahan sa Vieta theorem, na kung kailana =1 ang may anyo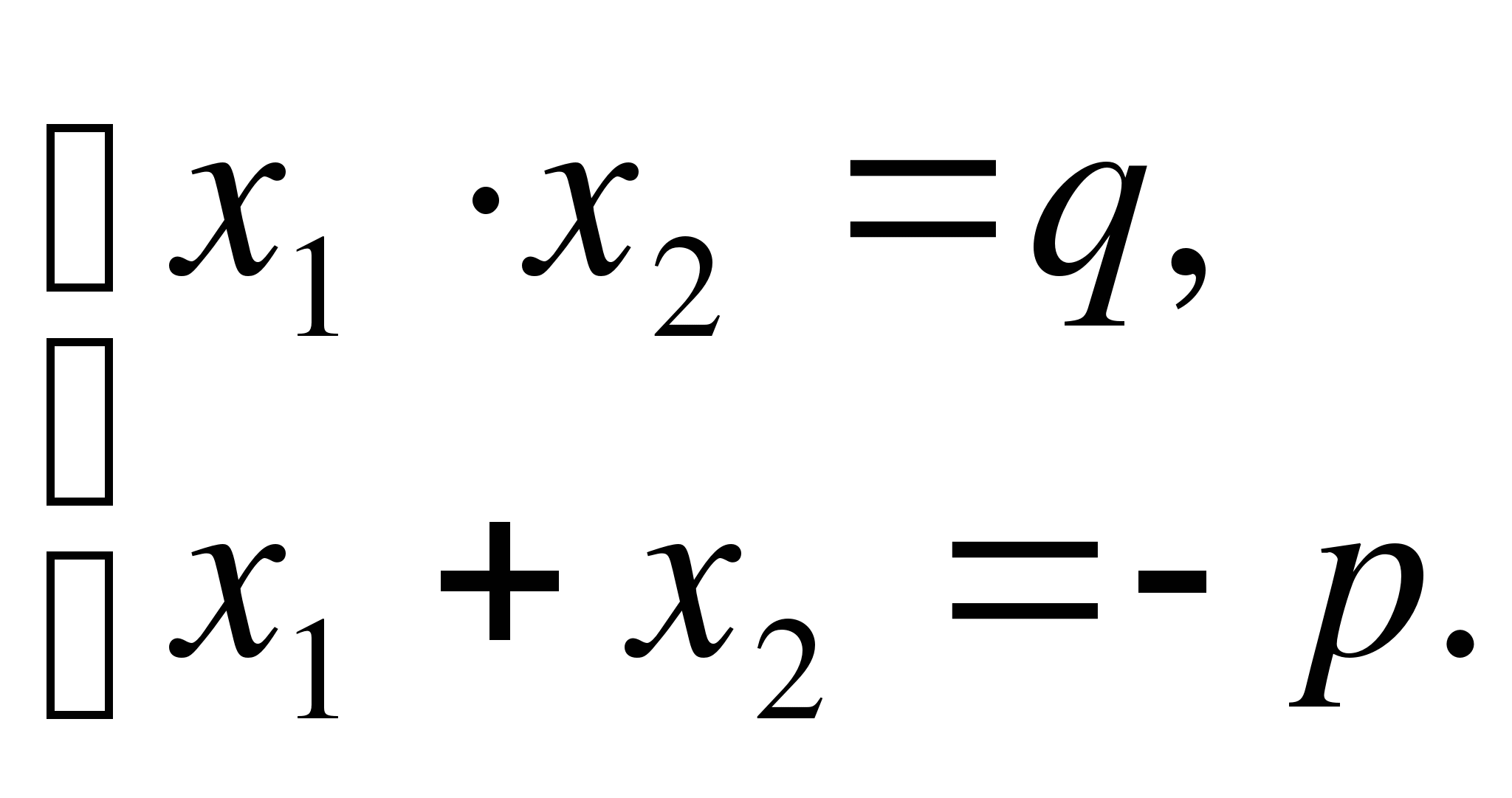

a) Kung isang libreng miyembroq ng ibinigay na quadratic equation ay positibo, pagkatapos ang equation ay may dalawang ugat at ito ay depende sa pangalawang koepisyentp . Kung ang p >0 , kung gayon ang parehong mga ugat ay negatibo kungp <0 , pagkatapos ang parehong mga ugat ay positibo.

Halimbawa 9

at

Halimbawa 10

at

b) Kung isang libreng miyembroq ng equation sa itaas ay negatibo, pagkatapos ang equation ay may dalawang ugat ng magkaibang tanda, at ang mas malaking ugat sa absolute value ay magiging positibo kungp <0, o negatibo kungp >0 .

Halimbawa 11.

at

Halimbawa 12.

at

Halimbawa 13

Hanapin ang mga ugat ng equation: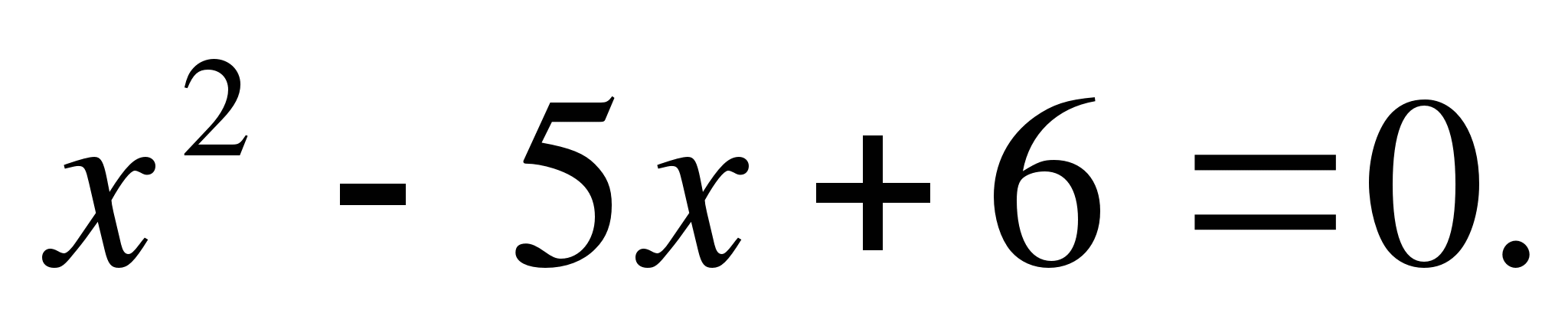

Solusyon: dito p=-5, q=6. Pumili ng dalawang numero x 1 at x 2 kaya

Ayon sa teorama ni Vieta

Sagot:

5. Mga katangian ng mga coefficient ng isang quadratic equation.

a) Hayaang ibigay ang quadratic equation

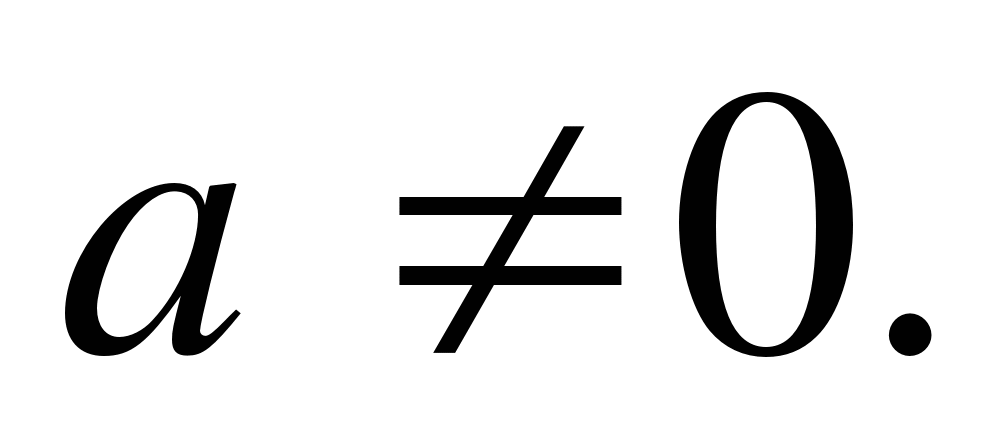
1. Kung ang a + b + c \u003d 0 (i.e. ang kabuuan ng mga coefficient ng equation ay zero), pagkatapos

Patunay: Hatiin ang magkabilang panig ng equation sa pamamagitan ngisang ≠ 0 , nakuha namin ang pinababang quadratic equation

Ayon sa teorama ni Vieta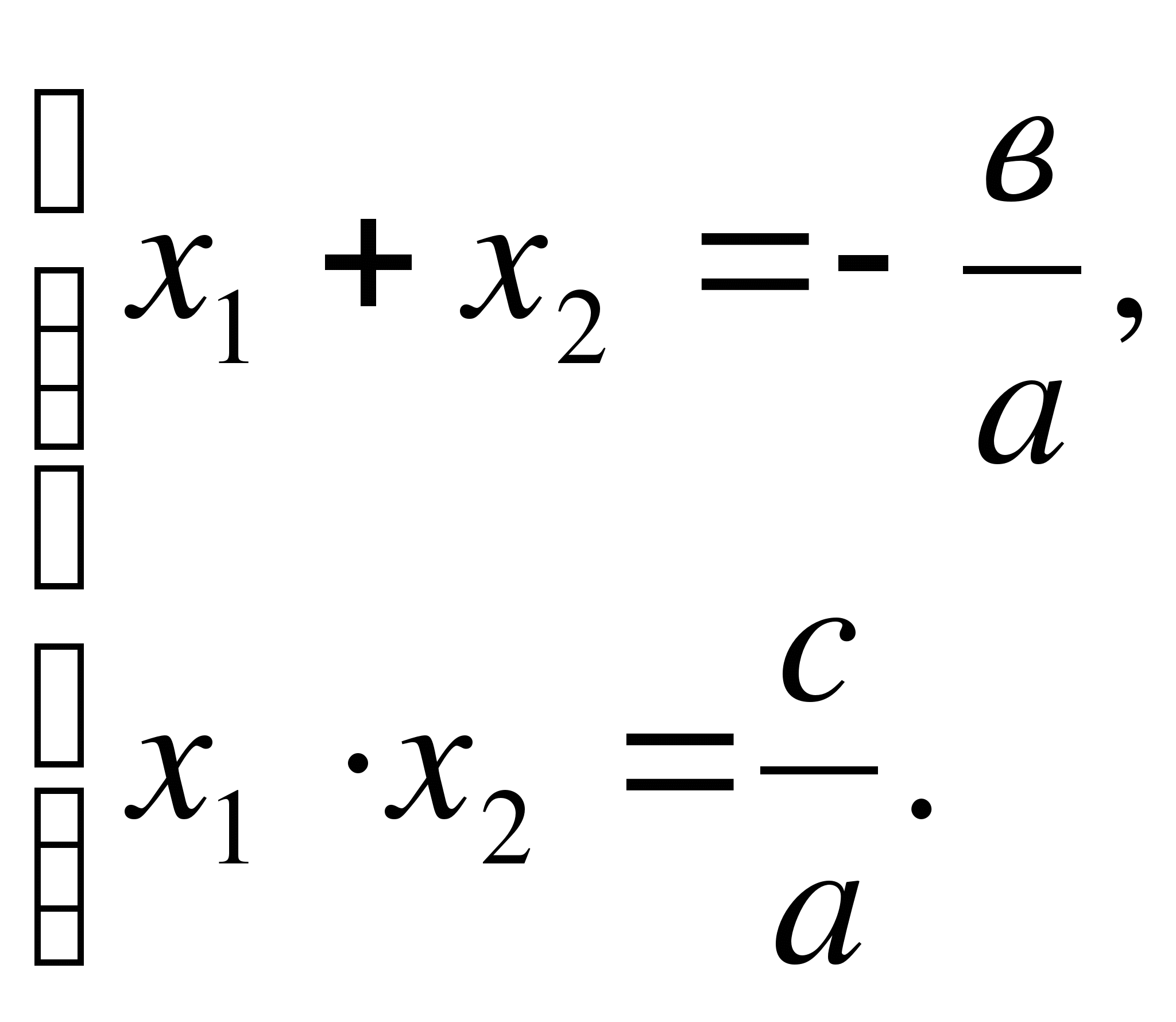

Sa pamamagitan ng kondisyon a + b + c = 0, saan c = - a - s. Ibig sabihin,

Nakukuha namin
Q.E.D.

2. Kung ang a - b + c \u003d 0, o b \u003d a + c, pagkatapos

Patunay: Ayon sa teorama ni Vieta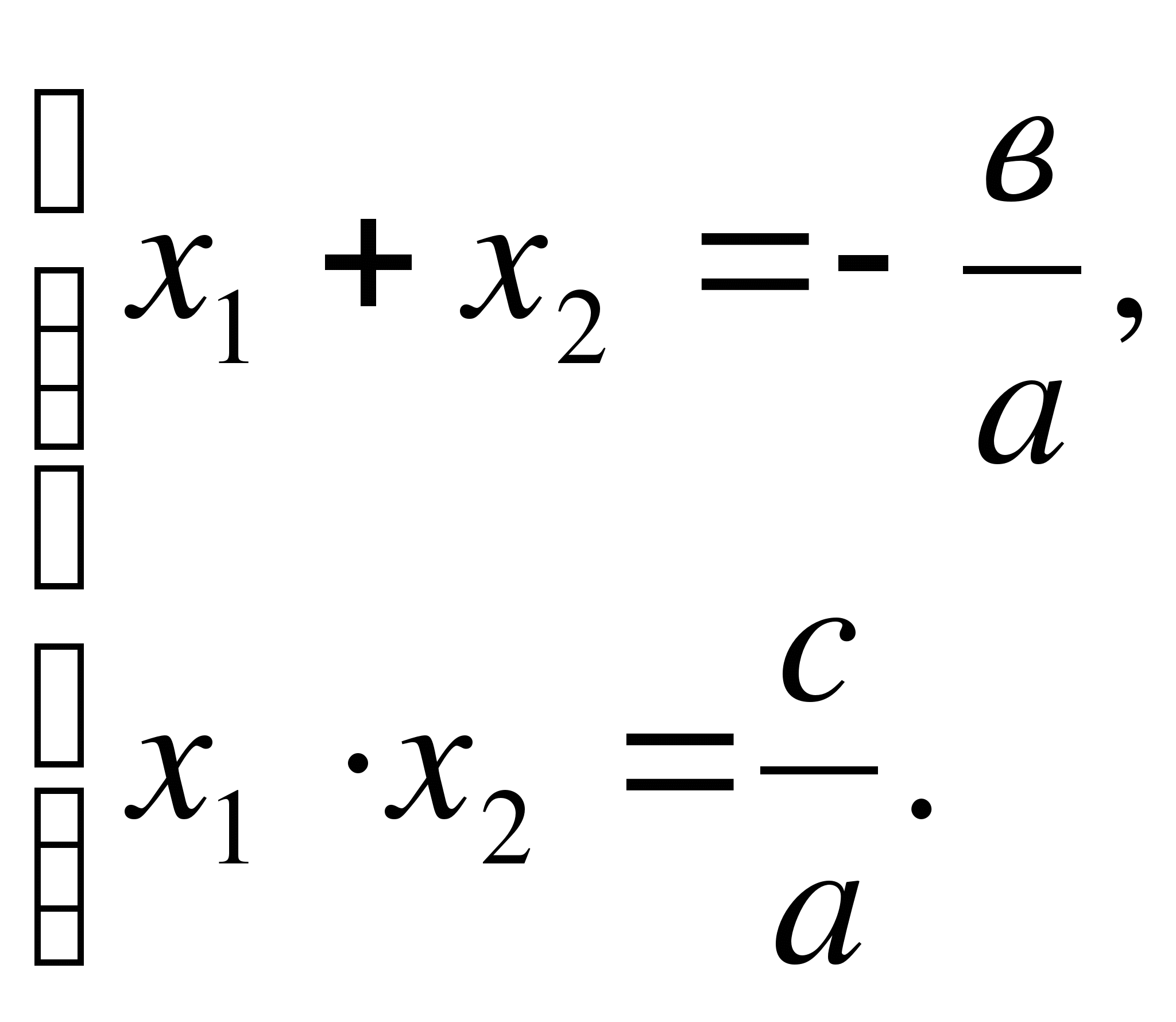

Sa pamamagitan ng kondisyon a - c + c = 0, saan c = a + c. kaya,

mga.
Q.E.D.

3. Kung sa equation

Patunay: Sa katunayan, ipinakita namin ang equation na ito sa anyo ng nabawasan

Isinulat namin ang equation sa form

Ang equation, na nakasulat sa form na ito, ay nagbibigay-daan sa iyo upang agad na makuha ang mga ugat

4. Kung ang a = - c = m · n , sa = m 2 – n 2 , kung gayon ang mga ugat ay may iba't ibang mga palatandaan, katulad:

Ang mga palatandaan sa harap ng mga fraction ay tinutukoy ng tanda ng pangalawang koepisyent.

6. Paglutas ng mga equation gamit ang "transfer" method.

Isaalang-alang ang quadratic equation

Oh 2 + b x + c= 0, at ≠ 0.

Pagpaparami ng magkabilang panig saa, makuha namin ang equation

a 2 X 2 + a b x + ac = 0.

Hayaan Oh= y, saan galing X = ; pagkatapos ay dumating tayo sa equation

sa 2 + sa pamamagitan ng + ac = 0,

katumbas ng isang ito.

mga ugat nito sa 1 at sa 2 hanapin sa tulong ng teorama ni Vieta. Sa wakas nakuha namin ang x 1 = sila 1 = . Sa pamamaraang ito, ang koepisyenta ay pinarami ng libreng termino, na parang "itinapon" dito, kung kaya't ito ay tinawagparaan ng paglipat. Ginagamit ang pamamaraang ito kapag madaling mahanap ang mga ugat ng isang equation gamit ang teorem ng Vieta at, higit sa lahat, kapag ang discriminant ay isang eksaktong parisukat.

Halimbawa 14

Lutasin ang equation: 2x 2 - 11x + 15 = 0.

Solusyon: "Ilipat" natin ang koepisyent 2 sa libreng termino, bilang resulta makuha natin ang equation:

sa 2 – 11 y + 30 = 0.

Ayon sa teorama ni Vieta

Sagot: 2,5; 3.

7. Graphic na solusyon quadratic equation.

Kung sa equation
ilipat ang pangalawa at pangatlong termino sa kanang bahagi, nakukuha namin

Bumuo tayo ng mga dependency graph
at

Ang graph ng unang dependence ay isang parabola na dumadaan sa pinanggalingan. Ang graph ng pangalawang dependence ay isang tuwid na linya (Larawan 1).

Posible ang mga sumusunod na kaso:

Ang isang tuwid na linya at isang parabola ay maaaring mag-intersect sa dalawang punto, ang abscissas ng mga intersection point ay ang mga ugat ng isang quadratic equation;

Ang linya at ang parabola ay maaaring hawakan (isang karaniwang punto lamang), i.e. ang equation ay may isang solusyon;

Ang tuwid na linya at ang parabola ay walang mga karaniwang punto, i.e. ang quadratic equation ay walang tunay na ugat. Halimbawa 15

Lutasin ang equation:2 x 2 + 6 x – 5 = 0.

Solusyon: Hatiin ang equation sa dalawang bahagi:y = 2 x 2 at y = 6 x – 5.

Bumuo tayo ng isang auxiliary table:

y = 2 x 2 -5

7

y = 6 x – 5

Bumuo tayo ng mga graph ng mga functiony = 2 x 2 at y = 6 x – 5.

Makikita sa graph na ang dalawang equation ay nagsalubong sa dalawang puntoX 1 sila 2 kaya ang equation ay magkakaroon ng dalawang ugatX 1 ≈ - 1.1 at x 2 ≈ 2,7.

Sagot: x 1 ≈ - 1.1 at x 2 ≈ 2.7.

8. Paglutas ng mga quadratic equation na may compass at straightedge.

Ang graphical na paraan upang malutas ang mga quadratic equation gamit ang isang parabola ay hindi maginhawa.

Kung bumuo ka ng isang parabola point by point, pagkatapos ay nangangailangan ng maraming oras, at ang antas ng katumpakan ng mga resulta na nakuha ay mababa.

Iminumungkahi namin ang sumusunod na pamamaraan para sa paghahanap ng mga ugat ng isang quadratic equation

gamit ang isang compass at isang ruler (Larawan 5).

Ipagpalagay natin na ang nais na bilog ay nag-intersect sa axis

abscissa sa mga punto B(X 1 ;0) at D(X 2 ;0), saan X 1 at X 2 ay ang mga ugat ng equation
at dumadaan sa mga puntong A(0;1) at C
sa y-axis. Pagkatapos ay sa pamamagitan ng teoramaosecant mayroon kaming OB OD= ОА OS, kung saan OS =

Ang gitna ng bilog ay nasa punto ng intersection ng mga patayoSF at SK, ibinalik sa mga midpoint ng chords AC at BD,Kaya pala

Kaya:

1) bumuo ng mga puntosS
(gitna ng bilog) at A(0;1);

2) gumuhit ng bilog na may radiusSA;

3) ang abscissas ng mga punto ng intersection ng bilog na ito na may axis OX ay ang mga ugat ng orihinal na quadratic equation.

Sa kasong ito, tatlong mga kaso ang posible.

1. Ang radius ng bilog ay mas malaki kaysa sa ordinate ng sentro
bumalandra ang bilog sa axis OX sa dalawang punto (Larawan 6a) B(X 1 ;0) at D(X 2 ;0), saan X 1 at X 2
1) Ang radius ng bilog ay mas malaki kaysa sa ordinate ng sentro
bumalandra ang bilog sa axis OX sa dalawang punto (Larawan 6a) B(X 1 ;0) at D(X 2 ;0), saan X 1 at X 2 ay ang mga ugat ng quadratic equation

2. Ang radius ng bilog ay katumbas ng ordinate ng sentro
ang bilog ay humipo sa O axisX (Larawan 6,b) sa punto B(X 1 ;0), saan X 1 ay ang ugat ng quadratic equation.

3. Ang radius ng bilog ay mas mababa sa ordinate ng sentro
ang bilog ay walang karaniwang mga punto na may abscissa axis (Larawan 6,sa ), sa kasong ito ang equation ay walang solusyon.

a)
dalawang ugatX 1 at X 2 .

b)
isang ugatX 1 .

sa)
Walang tunay na ugat.

Halimbawa 16

Lutasin ang equation:

Solusyon: tingnan ang fig.7.

Tukuyin ang mga coordinate ng gitna ng bilog sa pamamagitan ng mga formula:

Gumuhit tayo ng bilog na radiusSA, kung saan ang A (0; 1), S(1; -1).

Sagot: -1; 3.

Halimbawa 17.

Lutasin ang equation:
S tingnan ang Bradis V.M (lahat sa cm), mula sa pagkakatulad ng mga tatsulok

Halimbawa 20.

Para sa equation

z 2 – 9 z + 8 = 0.

Ang Nomogram ay nagbibigay ng mga ugat

z 1 = 8, 0 at z 2 = 1, 0 (Larawan 12).

Lutasin gamit ang isang nomogram

equation ng nomogram

2 z 2 – 9 z + 2 = 0.

Hatiin ang mga coefficient nito

equation sa pamamagitan ng 2, makuha namin ang equation

z 2 – 4, 5 + 1 = 0.

Ang Nomogram ay nagbibigay ng mga ugatz 1 = 4 atz 2 = 0,5.

Halimbawa 21.

Para sa equation

z 2 + 5 z – 6 = 0

nagbibigay ng nomogram positibo

ugatz 1 = 1.0 at negatibo

hanapin ang ugat sa pamamagitan ng pagbabawas

positibong ugat

mula sa– R, mga. z 2 = – R - 1 =

= – 5 – 1 = – 6.0 (Fig.13.)

10. Geometric na pamamaraan para sa paglutas ng mga quadratic equation.

Noong sinaunang panahon, kapag ang geometry ay mas binuo kaysa sa algebra, ang mga quadratic equation ay nalutas hindi sa algebraically, ngunit sa geometrically. Magbigay tayo ng isang halimbawa na naging tanyag mula sa Algebra ni al-Khwarizmi.

Halimbawa 22.

Lutasin ang equation x 2 + 10x = 39.

Sa orihinal, ang problemang ito ay binabalangkas tulad ng sumusunod: "Ang parisukat at sampung ugat ay katumbas ng 39."

Solusyon: Isaalang-alang ang isang parisukat na may gilid na x, ang mga parihaba ay binuo sa mga gilid nito upang ang kabilang panig ng bawat isa sa kanila ay 2, 2 = – 8.

y 3

sa 2

3y

3y

9

3

Halimbawa 24.

Lutasin ang mga equation sa geometrical na paraan 2 – 6y – 16 = 0.

Pagbabago ng equation, nakukuha namin

sa 2 - 6y \u003d 16.

Sa fig. hanapin ang "mga imahe" ng expression na y 2 - 6y, ibig sabihin. mula sa lugar ng isang parisukat na may gilidsa Ibawas ang lugar ng isang parisukat na may gilid na katumbas ng 3 dalawang beses.

Kaya, kung ang expression na y 2 - 6y magdagdag ng 9, pagkatapos ay makuha namin ang lugar ng isang parisukat na may gilid y - 3. Pinapalitan ang expression na y 2 - 6y katumbas nito, nakukuha natin ang: (y - 3) 2 = 16 +9, ibig sabihin. y – 3 = ±
o y - 3 = ± 5, kung saan y 1 = 8 at y 2 = – 2.

y 3

y - 3

y - 3

3

3

9

IV. KONGKLUSYON

Bilang resulta ng gawaing ito, ang mga sumusunod na konklusyon ay maaaring iguguhit:

Ang pag-aaral ng siyentipiko at metodolohikal na panitikan sa paksa ng gawaing isinagawa ay nagpakita na ang paggamit ng iba't ibang mga pamamaraan para sa paglutas ng mga quadratic equation ay isang mahalagang link sa pag-aaral ng matematika, nagpapataas ng interes, nagkakaroon ng atensyon at talino.

Ang sistema ng paggamit ng iba't ibang paraan ng paglutas ng mga equation sa iba't ibang yugto ng aralin ay isang epektibong paraan ng pag-activate ng mga mag-aaral, may positibong epekto sa pagpapabuti ng kalidad ng kaalaman, kasanayan, at pagbuo ng aktibidad ng pag-iisip.

Ang pangunahing bagay sa paglutas ng mga quadratic equation ay ang piliin ang tamang rational na paraan ng paglutas at ilapat ang solusyon algorithm.

Ang gawain sa paksang ito ay nakakatulong sa karagdagang pag-aaral ng iba't ibang paraan ng paglutas ng iba't ibang equation.

v.PANITIKAN

Great Soviet Encyclopedia.– M., Soviet Encyclopedia, 1974.

Pahayagang "Matematika".– Publishing house "Una ng Setyembre".

Glazer G.I. Kasaysayan ng matematika sa paaralan. 7-8 na klase.– M., Edukasyon, 1982.

Ensiklopedya ng mga bata. T. 2.– M., Pedagogy,1972.

Dorofeeva VA. Mga pahina ng kasaysayan sa mga aralin sa matematika.– Lvov, Quantor,1991.

Liman M.M. Mga mag-aaral tungkol sa matematika at mathematician.– M., Enlightenment,1981.

Encyclopedia para sa mga bata.– M., Avanta +, 1997.

Alimov Sh.A., Ilyin V.A. et al. Algebra, 6-8. Teksbuk ng pagsubok para sa mga baitang 6-8 mataas na paaralan. – M., Enlightenment,1981. ;

Bradis V.M. Apat na digit mga talahanayan sa matematika para sa high school. Ed. ika-57.– M., Enlightenment,1990. S. 83.

Zlotsky G.V. Mga task card sa pagtuturo ng matematika. Ang libro para sa guro.– M., Edukasyon, 1992.

Klyukvin M.F. Algebra, 6-8. Tulong ng mag-aaral6-8 mga klase.– M., Edukasyon, 1963.

Kuzhepov A.K., Rubanov A.T. Algebra at elementarya na pag-andar. Pagtuturo para sa pangalawang espesyal institusyong pang-edukasyon. – M., mataas na paaralan1969.

Matematika (dagdag sa pahayagan na "Pervoe september"), Blg. 21/96, 10/97, 24/97, 18/98, 21/98.

Okunev A.K.. Quadratic function, mga equation at hindi pagkakapantay-pantay. Isang gabay para sa guro.– M., Edukasyon, 1972.

Presman AA.Paglutas ng isang quadratic equation na may compass at straightedge.– M., Kvant, No. 4/72. S. 34.

SolomnikB. C., Miloye P.I. Koleksyon ng mga tanong at gawain sa matematika. Ed. Ika-4, idagdag.– M., graduate School, 1973.

Khudobin A.I.. Koleksyon ng mga problema sa algebra at elementary functions. Isang gabay para sa guro. Ed. ika-2.– M., Edukasyon, 1970.

Lit.Pentkovsky M.V., Nagbibilang ng mga guhit. (Nomograms), 2nd ed., M., 1959;

Proyekto
malikhaing pangalan ng proyekto
Motto: Sa matematika, ang maliliit na pandaraya ay may malaking papel.
May-akda ng proyekto: Rylova Victoria
estudyante ng 8G class MOU secondary school No
na may malalim na pag-aaral
indibidwal na mga item "Polyforum"

Ang pangunahing tanong ng proyekto:
Gaano iba-iba ang mga solusyon
quadratic equation?
Hypothesis:
Sa palagay ko ang mga quadratic equation ay maaaring malutas
sa iba't ibang paraan
Target:
Ang pag-aaral ng mga teoretikal na pundasyon at aplikasyon sa
magsanay ng iba't ibang paraan ng paglutas ng parisukat
mga equation

Mga gawain:
1. Kumuha ng impormasyon sa paksa mula sa nakasulat
mga mapagkukunan at sa Internet
2. I-synthesize ang impormasyon ayon sa plano
3. Tuklasin ang iba't ibang paraan upang malutas ang square
mga equation at subukan ang materyal sa pagsasanay
Plano ng trabaho:
Kahulugan ng paksa at layunin ng proyekto,
pagbabalangkas ng paksa ng pananaliksik
Pagtukoy sa pinagmulan ng impormasyon
Pagtukoy kung paano mangolekta at mag-analisa
impormasyon
Pagtukoy sa Paraan ng Paglalahad
resulta

anotasyon

Proyekto "Mga pamamaraan para sa paglutas ng parisukat
equation" ay sumasalamin sa mga resulta ng pag-aaral,
isinagawa ko tungkol sa kung ano ang umiiral
mga paraan upang malutas ang mga quadratic equation at kung ano ang
ito ay maaari mong kunin na kapaki-pakinabang para sa iyong sarili at sa akin
mga kaibigan.
Ang tema ng proyekto ay may kaugnayan sa paggamit
mga paraan upang malutas ang mga quadratic equation
hanapin ang hindi alam tungkol sa alam.
Ang matematika ay itinuturo sa paaralan
mga formula para sa mga ugat ng quadratic equation, na may
na maaaring magamit upang malutas ang anuman
quadratic equation.
Gayunpaman, may iba pang mga solusyon
equation na nagbibigay-daan sa iyo upang napakabilis at
makatwirang lutasin ang mga quadratic equation.

Mula sa kasaysayan ng parisukat
mga equation
Ang mga parisukat na equation ay nalutas nang humigit-kumulang 2000 taon
BC e. Babylonians. Paglalapat ng moderno
algebraic notation, masasabi natin na sa kanilang
Ang mga tekstong cuneiform ay matatagpuan, maliban sa mga hindi kumpleto, at
tulad ng kumpletong quadratic equation:
Halos lahat ng mga sinulat na cuneiform ay natagpuan sa ngayon
Ang mga teksto ay nagbibigay lamang ng mga problema sa mga solusyon,
nakasaad sa anyo ng mga reseta, nang walang mga tagubilin
tungkol sa kung paano sila
natagpuan.

iskolar ng India na si Brahmagupta (ika-7 siglo),
binalangkas ang pangkalahatang tuntunin ng hinlalaki
quadratic equation binawasan sa
solong kanonikal na anyo:
ax2 + bx = c, a > 0
Sa equation, ang mga coefficient, maliban sa a,
maaaring negatibo. tuntunin
Ang Brahmagupta ay mahalagang kapareho ng
atin.
Brahmagupta
Mga formula para sa paglutas ng mga quadratic equation
ay unang nai-publish sa isang libro
isinulat ng isang Italian mathematician
Leonardo Fibonacci (XIII siglo). x2 + bx = c,
kasama ang lahat ng posibleng kumbinasyon ng mga palatandaan
coefficients b, c ay
nabuo lamang sa Europa noong 1544.
Leonardo Fibonacci

Lamang sa siglo XVII. salamat sa gawa nina Girard, Descartes, Newton at
paraan ng ibang mga siyentipiko sa paglutas ng mga quadratic equation
nagkakaroon ng modernong hitsura.
Sa tingin ko
kaya naman,
umiral.
Descartes
May henyo
iniisip ang pasensya,
nakatutok
sa sikat
direksyon.
Newton
Lahat ng Equation
mayroon ang mga algebra
napakaraming desisyon
ilan
mga palabas
Pangalan
pinakamataas
dami.
Girard
Lahat ng mathematicians
alam na sa ilalim
nakatago ang algebra
walang kapantay
kayamanan, ngunit
nagawang hanapin sila
viet

Geometric
paraan ng solusyon
parisukat
mga equation
Desisyon
parisukat
mga equation
sa pamamagitan ng
mga nomogram
Desisyon
parisukat
mga equation
gamit ang isang bilog
at mga pinuno
Mga solusyon
parisukat
mga equation
paraan
"mga paglilipat"
Pagkabulok
umalis
mga bahagi ng equation
mga multiplier
Iba-iba
mga paraan
mga solusyon
parisukat
mga equation
Graphic
desisyon
parisukat
mga equation
Pamamaraan
alokasyon
buong parisukat
Pamamaraan
coefficients
Desisyon
parisukat
mga equation
ayon sa pormula
Desisyon
mga equation
gamit
Mga teorema ni Vieta

1. PARAAN: Pagfactor sa kaliwang bahagi ng equation

Target:
magbigay ng quadratic equation
pangkalahatang view upang tingnan
A(x) B(x)=0,
kung saan ang A(x) at B(x) -
polynomial na may paggalang sa x.
Mga paraan:
Tinatanggal ang karaniwang kadahilanan para sa
panaklong;
Paggamit ng mga formula
pinaikling multiplikasyon;
paraan ng pagpapangkat.
Solusyonan natin ang equation
x2 + 10x - 24 = 0.
I-factorize natin ang kaliwang bahagi:
x2 + 10x - 24 =
\u003d (x + 12) (x - 2).
Kaya naman,
(x + 12)(x - 2) = 0
Dahil ang produkto ay zero, kung gayon
ang isa sa mga kadahilanan nito ay katumbas ng zero. Samakatuwid ang kaliwang bahagi
Ang equation ay naglalaho sa x = 2, at gayundin sa x = - 12.
Nangangahulugan ito na ang numero 2 at - 12 ay mga ugat
mga equation x2 + 10x - 24 = 0.

2. PARAAN: Buong parisukat na paraan ng pagpili.

Ang kakanyahan ng pamamaraan: magdala ng pangkalahatang quadratic equation sa
hindi kumpletong quadratic equation.
Lutasin natin ang equation na x2 + 6x - 7 = 0.
Pumili tayo ng isang buong parisukat sa kaliwang bahagi.
Binabago namin ngayon ang kaliwang bahagi ng equation
x2 + 6x - 7 = 0, pagdaragdag dito at pagbabawas ng 9.
Meron kami:
x2 + 6x - 7 =
\u003d x2 + 2 x 3 + 9 - 9 - 7 \u003d
\u003d (x + 3) 2 - 9 - 7 \u003d (x + 3) 2 - 16.
Kaya, ang equation na ito ay maaaring isulat
Kaya:
(x + 3) 2 - 16 \u003d 0,
(x + 3)2 = 16.
Samakatuwid, x + 3 - 4 = 0, o x + 3 = -4
x1 = 1,
x2 = -7.

3. PARAAN: Paglutas ng parisukat
equation ayon sa formula
a 1
b 0, c 0
D>0
2 ugat
D=0
1 ugat
x px g 0
2
D<0 Нет корней
Mga formula ng ugat:
2
1
x1.2
p
2
b b 2 4ac
x1, 2
;
2a
2
p
g;
4
3
x1, 2
k k 2 ac
a

4. PARAAN: Paglutas ng mga equation gamit ang Vieta theorem.

Tulad ng nalalaman, ang ibinigay na quadratic equation ay may anyo
x2 + px + c = 0. (1)
Ang mga ugat nito ay nagbibigay-kasiyahan sa Vieta theorem, na para sa a = 1 ay may anyo
x1 x2 = q,
Mula dito maaari nating iguhit ang mga sumusunod na konklusyon
x1 + x2 = -p
(mula sa mga coefficient p at q ay mahuhulaan ng isa ang mga palatandaan
mga ugat).
Kung (q > 0), kung gayon ang equation ay may dalawang magkapareho
tanda ng ugat, at ito ang inggit ng pangalawang koepisyent p.
Kung p< 0, то оба корня отрицательны.
Kung p< 0, то оба корня положительны.

5. PARAAN: Paglutas ng mga equation gamit ang "transfer" method.

Sa pamamaraang ito, ang koepisyent a ay pinarami ng libreng termino, na parang
"itinapon" sa kanya, kaya tinawag itong paraan ng "paglipat".
Ginagamit ang paraang ito kapag madaling mahanap ang mga ugat ng equation,
gamit ang Vieta theorem at, higit sa lahat, kapag ang discriminant ay
perpektong parisukat
Lutasin natin ang equation na 2x2 - 11x + 15 = 0.
"Itapon" natin ang koepisyent 2 sa libreng termino, sa
bilang isang resulta makuha namin ang equation
y2 - 11y + 30 = 0.
Ayon sa Vieta theorem y \u003d 5, y \u003d 6, pagkatapos x1 \u003d 5/2, x \u003d 6/2
Sagot: 2.5; 3.

6. PARAAN: Mga katangian ng mga coefficient ng isang quadratic equation

Hayaan ang quadratic equation
ax2 + bx + c = 0, kung saan ang isang ≠ 0.
Kung, a + b + c \u003d 0, kung gayon
x1 1, x2
c
a
Kung b = a + c, kung gayon
x1 1, x2
c
a
1978x1984x60
2
x1 1;
6
x2
1978
319 x 2 1988 x 1669 0
x1 1;
1669
x2
.
319

7. PARAAN: Graphical na solusyon ng isang quadratic equation

ibahin ang anyo ng equation
x2 + px + q = 0
x2 = - px - q.
Bumuo tayo ng mga graph ng dependence y \u003d x2 at y \u003d - px - q.
Ang graph ng unang dependence ay isang parabola passing
sa pamamagitan ng pinagmulan. Iskedyul ng dalawa
dependencies - tuwid na linya (Larawan 1). Posible ang mga sumusunod
kaso:
Direkta at
lata ng parabola
hawakan (lamang
isang karaniwan
tuldok), ibig sabihin.
may equation
isang solusyon;
tuwid at
parabola ay hindi
may mga karaniwang puntos
mga. parisukat
ang equation ay hindi
mga ugat.
tuwid na linya at parabola
maaaring magsalubong
dalawang puntos, abscissa
puntos
mga interseksyon
ay
mga ugat
parisukat
mga equation;

8. PARAAN: Paglutas ng mga quadratic equation gamit ang compass at ruler.

ax2 + bx + c = 0
Kaya:
1) bumuo ng mga punto (gitna ng bilog)
at A(0; 1);
2) gumuhit ng bilog na may radius
SA;
3) ang abscissas ng mga punto ng intersection nito
ang mga bilog na may x-axis ay
mga ugat ng orihinal na parisukat
mga equation.
2) hinawakan ng bilog ang x-axis sa
Sa kasong ito, tatlong mga kaso ang posible.
1) ang bilog ay bumalandra sa axis
Ox sa dalawang puntos
B(x1; 0) at D(x2; 0), kung saan ang x1 at x2
- mga parisukat na ugat
equation ax² + bx + c = 0.
punto B(x1; 0), kung saan ang x1 ay ang ugat
quadratic equation.
3) ang bilog ay walang karaniwan
mga puntos na may abscissa axis (Larawan 6, c), sa
Sa kasong ito, ang equation ay hindi
mga solusyon.

9. PARAAN: Paglutas ng mga quadratic equation gamit ang isang nomogram.

Talahanayan XXII. p.83 (tingnan ang Bradis V.M. Four-digit
mga talahanayan ng matematika. - M., Enlightenment,
1990).
Nomogram para sa Paglutas ng Equation
z2 + pz + q = 0. Ang nomogram na ito ay nagpapahintulot,
nang hindi nilulutas ang isang quadratic equation,
matukoy ang mga ugat ng equation sa pamamagitan ng mga coefficient nito.
Ang curvilinear scale ng nomogram ay binuo
ayon sa mga formula (Larawan 11):
z2 + pz + q = 0,
kung saan ang letrang z ay nangangahulugang ang etiketa ng alinman
mga curved scale point.

10. PARAAN: Geometrical na paraan
mga solusyon ng quadratic equation.
Paano nalutas ng mga sinaunang Griyego
equation y2 + 6y - 16 = 0.
Ang solusyon ay iniharap sa
figure, kung saan y2 + 6y = 16,
o y2 + 6 y + 9 = 16 + 9.
Mga ekspresyong y2 + 6y + 9 at 16 + 9
kumakatawan sa geometriko
ay ang parehong parisukat, at
orihinal na equation y2 + 6y - 16
+ 9 - 9 = 0 - pareho
ang equation. Mula sa kung saan kami kumukuha
na y + 3 = + 5 at y + 3 = -5, o
y=2, y2= -8
sa
3
sa
y2
3
3y
3y
9

ginagawang posible ng aking trabaho
tingnan ang mga hamon na
may mathematics tayo.
nararapat ang mga solusyong ito
pansin
dahil hindi sila nasasalamin sa
mga aklat-aralin sa paaralan ng matematika;
Ang pag-master ng mga teknik na ito ay nakakatulong sa akin
makatipid ng oras at malutas nang mahusay
mga equation;
kailangan ng mabilis na solusyon
dahil sa paggamit ng isang sistema ng pagsubok
huling pagsusulit;

Konklusyon

“Sa mathematics, hindi dapat tandaan
mga formula, ngunit mga proseso ng pag-iisip"
V.P. Ermakov

Kopyevskaya rural secondary school

10 Paraan para Malutas ang Mga Quadratic Equation

Pinuno: Patrikeeva Galina Anatolyevna,

guro sa matematika

s.Kopyevo, 2007

1. Kasaysayan ng pagbuo ng mga quadratic equation

1.1 Quadratic equation sa sinaunang Babylon

1.2 Paano pinagsama-sama at nalutas ni Diophantus ang mga quadratic equation

1.3 Mga parisukat na equation sa India

1.4 Quadratic equation sa al-Khwarizmi

1.5 Quadratic equation sa Europe XIII - XVII siglo

1.6 Tungkol sa teorama ni Vieta

2. Mga pamamaraan para sa paglutas ng mga quadratic equation

Konklusyon

Panitikan

1. Kasaysayan ng pagbuo ng mga quadratic equation

1.1 Quadratic equation sa sinaunang Babylon

Ang pangangailangan upang malutas ang mga equation hindi lamang ng una, kundi pati na rin ng pangalawang degree sa sinaunang panahon ay sanhi ng pangangailangan upang malutas ang mga problema na may kaugnayan sa paghahanap ng mga lugar ng lupa at earthworks ng isang militar na kalikasan, pati na rin ang pag-unlad ng astronomy at matematika mismo. Ang mga quadratic equation ay nagawang malutas ang mga 2000 BC. e. Babylonians.

Gamit ang modernong algebraic notation, masasabi natin na sa kanilang mga cuneiform na teksto, bilang karagdagan sa mga hindi kumpleto, mayroong tulad, halimbawa, kumpletong quadratic equation:

X2 + X= ¾; X2 - X= 14,5

Ang tuntunin para sa paglutas ng mga equation na ito, na nakasaad sa mga tekstong Babylonian, ay talagang kasabay ng modernong isa, ngunit hindi alam kung paano napunta ang mga Babylonians sa panuntunang ito. Halos lahat ng mga tekstong cuneiform na natagpuan sa ngayon ay nagbibigay lamang ng mga problema sa mga solusyon na nakasaad sa anyo ng mga recipe, na walang indikasyon kung paano sila natagpuan.

Sa kabila ng mataas na antas ng pag-unlad ng algebra sa Babylon, ang mga tekstong cuneiform ay kulang sa konsepto ng negatibong numero at mga pangkalahatang pamamaraan para sa paglutas ng mga quadratic equation.

1.2 Paano pinagsama-sama at nalutas ni Diophantus ang mga quadratic equation.

Ang Arithmetic ng Diophantus ay hindi naglalaman ng isang sistematikong paglalahad ng algebra, ngunit naglalaman ito ng isang sistematikong serye ng mga problema, na sinamahan ng mga paliwanag at nalutas sa pamamagitan ng pagbabalangkas ng mga equation ng iba't ibang antas.

Kapag nag-compile ng mga equation, mahusay na pinipili ni Diophantus ang mga hindi alam upang gawing simple ang solusyon.

Narito, halimbawa, ang isa sa kanyang mga gawain.

Gawain 11."Maghanap ng dalawang numero na alam na ang kanilang kabuuan ay 20 at ang kanilang produkto ay 96"

Nagtatalo si Diophantus bilang mga sumusunod: sumusunod ito mula sa kondisyon ng problema na ang mga nais na numero ay hindi pantay, dahil kung sila ay pantay, kung gayon ang kanilang produkto ay magiging katumbas ng hindi sa 96, ngunit sa 100. Kaya, ang isa sa kanila ay higit sa kalahati ng kanilang kabuuan, ibig sabihin. 10+x, ang isa ay mas maliit, i.e. 10's. Ang pagkakaiba sa pagitan nila 2x.

Kaya ang equation:

(10 + x)(10 - x) = 96

100's 2 = 96

X 2 - 4 = 0 (1)

Mula rito x = 2. Isa sa mga gustong numero ay 12 , iba pa 8 . Desisyon x = -2 para sa Diophantus ay hindi umiiral, dahil ang Griyego matematika alam lamang positibong numero.

Kung malulutas natin ang problemang ito sa pamamagitan ng pagpili ng isa sa mga nais na numero bilang hindi alam, pagkatapos ay darating tayo sa solusyon ng equation

y(20 - y) = 96,

sa2 - 20y + 96 = 0. (2)

Malinaw na pinasimple ni Diophantus ang solusyon sa pamamagitan ng pagpili ng kalahating pagkakaiba ng mga nais na numero bilang hindi alam; nagagawa niyang bawasan ang problema sa paglutas ng hindi kumpletong quadratic equation (1).

1.3 Quadratic equation sa India

Ang mga problema para sa quadratic equation ay matatagpuan na sa astronomical tract na "Aryabhattam", na pinagsama-sama noong 499 ng Indian mathematician at astronomer na si Aryabhatta. Ang isa pang siyentipikong Indian, si Brahmagupta (ika-7 siglo), ay nagbalangkas ng pangkalahatang tuntunin para sa paglutas ng mga quadratic equation na binawasan sa isang solong canonical form:

Oh2 + bx = c, a > 0. (1)

Sa equation (1), ang mga coefficient, maliban sa a, maaari ding maging negatibo. Ang pamumuno ni Brahmagupta ay esensyal na tumutugma sa atin.

Sa sinaunang India, ang mga pampublikong kumpetisyon sa paglutas ng mahihirap na problema ay karaniwan. Sa isa sa mga lumang aklat ng India, ang mga sumusunod ay sinabi tungkol sa gayong mga kompetisyon: “Kung paanong ang araw ay nanggagaling sa mga bituin sa taglay nitong kinang, gayundin ang isang may-aral na tao ay hihigit sa kaluwalhatian ng iba sa mga pampublikong pagpupulong, na nagmumungkahi at naglutas ng mga problema sa algebraic.” Ang mga gawain ay kadalasang binibihisan sa anyong patula.

Narito ang isa sa mga problema ng sikat na Indian mathematician ng XII century. Bhaskara.

Gawain 13.

"Isang makulit na kawan ng mga unggoy At labindalawa sa mga baging ...

Pagkakain ng kapangyarihan, nagsaya. Nagsimula silang tumalon, nakabitin ...

Walong bahagi ng mga ito sa isang parisukat Ilang unggoy ang naroon,

Nagsasaya sa parang. Sabihin mo sa akin, sa kawan na ito?

Ang solusyon ni Bhaskara ay nagpapahiwatig na alam niya ang tungkol sa dalawang pagpapahalaga ng mga ugat ng quadratic equation (Larawan 3).

Ang equation na tumutugma sa problema 13 ay:

(x/8) 2 + 12 = x

Sumulat si Bhaskara sa ilalim ng pagkukunwari ng:

X2 - 64x = -768

at, upang makumpleto ang kaliwang bahagi ng equation na ito sa isang parisukat, idinagdag niya ang magkabilang panig 32 2 , pagkuha pagkatapos:

X2 - 64x + 322 = -768 + 1024,

(x - 32)2 = 256,

x - 32 = ± 16,

X1 = 16, x2 = 48.

1.4 Quadratic equation sa al-Khorezmi

Ang algebraic treatise ni Al-Khorezmi ay nagbibigay ng klasipikasyon ng linear at quadratic equation. Ang may-akda ay naglista ng 6 na uri ng mga equation, na nagpapahayag ng mga ito bilang mga sumusunod:

1) "Ang mga parisukat ay katumbas ng mga ugat", i.e. Oh2 + kasama ang =bX.

2) "Ang mga parisukat ay katumbas ng numero", i.e. Oh2 = s.

3) "Ang mga ugat ay katumbas ng bilang", i.e. ah = s.

4) "Ang mga parisukat at numero ay katumbas ng mga ugat", i.e. Oh2 + kasama ang =bX.

5) "Ang mga parisukat at ugat ay katumbas ng bilang", i.e. Oh2 + bx= s.

6) "Ang mga ugat at numero ay katumbas ng mga parisukat", i.e.bx+ c = palakol2 .

Para kay al-Khwarizmi, na umiwas sa paggamit ng mga negatibong numero, ang mga tuntunin ng bawat isa sa mga equation na ito ay mga addend, hindi mga pagbabawas. Sa kasong ito, ang mga equation na walang positibong solusyon ay malinaw na hindi isinasaalang-alang. Binabalangkas ng may-akda ang mga pamamaraan para sa paglutas ng mga equation na ito, gamit ang mga pamamaraan ng al-jabr at al-muqabala. Ang kanyang mga desisyon, siyempre, ay hindi ganap na nag-tutugma sa atin. Hindi sa banggitin ang katotohanan na ito ay purong retorika, dapat itong tandaan, halimbawa, na kapag nilutas ang isang hindi kumpletong quadratic equation ng unang uri

Si al-Khorezmi, tulad ng lahat ng mathematician bago ang ika-17 siglo, ay hindi isinasaalang-alang ang zero na solusyon, marahil dahil ito ay hindi mahalaga sa mga partikular na praktikal na problema. Kapag nilulutas ang kumpletong quadratic equation ng al - Khorezmi sa bahagyang mga halimbawa ng numero itinakda ang mga tuntunin ng desisyon, at pagkatapos ay ang mga geometric na patunay.

Gawain 14.“Ang parisukat at ang bilang na 21 ay katumbas ng 10 ugat. Hanapin ang ugat" (ipagpalagay na ang ugat ng equation x2 + 21 = 10x).

Ang solusyon ng may-akda ay ganito: hatiin ang bilang ng mga ugat sa kalahati, makakakuha ka ng 5, i-multiply ang 5 sa sarili nito, ibawas ang 21 sa produkto, 4 ang natitira. Kunin ang ugat ng 4, makakakuha ka ng 2. Ibawas ang 2 sa 5, ikaw makakuha ng 3, ito ang magiging ninanais na ugat. O magdagdag ng 2 hanggang 5, na magbibigay ng 7, ito ay ugat din.

Ang Treatise al - Khorezmi ay ang unang libro na dumating sa amin, kung saan ang pag-uuri ng mga quadratic equation ay sistematikong nakasaad at ibinigay ang mga formula para sa kanilang solusyon.

1.5 Quadratic equation sa EuropeXIII- XVIImga siglo

Ang mga formula para sa paglutas ng mga quadratic equation sa modelo ng al - Khorezmi sa Europa ay unang itinakda sa "Book of the Abacus", na isinulat noong 1202 ng Italyano na matematiko na si Leonardo Fibonacci. Ang malaking gawaing ito, na sumasalamin sa impluwensya ng matematika, kapwa ang mga bansa ng Islam at Sinaunang Greece, ay naiiba sa parehong pagkakumpleto at kalinawan ng presentasyon. Ang may-akda ay nakapag-iisa na bumuo ng ilang mga bagong algebraic na halimbawa ng paglutas ng problema at siya ang una sa Europa na lumapit sa pagpapakilala ng mga negatibong numero. Ang kanyang libro ay nag-ambag sa paglaganap ng algebraic na kaalaman hindi lamang sa Italya, kundi pati na rin sa Alemanya, Pransya at iba pang mga bansa sa Europa. Maraming mga gawain mula sa "Aklat ng Abacus" ang pumasa sa halos lahat ng mga aklat-aralin sa Europa noong ika-16 - ika-17 siglo. at bahagyang XVIII.

PAGE_BREAK--

Ang pangkalahatang tuntunin para sa paglutas ng mga quadratic equation ay binawasan sa isang solong canonical form:

X2 + bx= kasama,

para sa lahat ng posibleng kumbinasyon ng mga palatandaan ng mga coefficient b, kasama ay binuo sa Europa lamang noong 1544 ni M. Stiefel.

Ang Vieta ay may pangkalahatang derivation ng formula para sa paglutas ng isang quadratic equation, ngunit ang Vieta ay kumikilala lamang ng mga positibong ugat. Ang mga Italian mathematician na sina Tartaglia, Cardano, Bombelli ay kabilang sa mga una noong ika-16 na siglo. Isaalang-alang, bilang karagdagan sa positibo, at negatibong mga ugat. Lamang sa siglo XVII. Salamat sa gawa nina Girard, Descartes, Newton at iba pang mga siyentipiko, ang paraan upang malutas ang mga quadratic equation ay nagkakaroon ng modernong hitsura.

1.6 Tungkol sa teorama ni Vieta

Ang theorem na nagpapahayag ng relasyon sa pagitan ng mga coefficient ng isang quadratic equation at ang mga ugat nito, na may pangalang Vieta, ay binuo niya sa unang pagkakataon noong 1591 bilang mga sumusunod: "Kung B+ D pinarami ng A- A2 , katumbas BD, pagkatapos A katumbas AT at pantay D».

Upang maunawaan ang Vieta, dapat tandaan iyon PERO, tulad ng anumang patinig, para sa kanya ang hindi kilala (aming X), ang mga patinig SA,D- mga coefficient para sa hindi alam. Sa wika ng modernong algebra, ang pormulasyon ni Vieta sa itaas ay nangangahulugang: kung

(isang +b)x - x2 = ab,

X2 - (isang +b)x + ab= 0,

X1 = a, x2 = b.

Pagpapahayag ng ugnayan sa pagitan ng mga ugat at coefficient ng mga equation pangkalahatang mga formula, nakasulat gamit ang mga simbolo, itinatag ng Viet ang pagkakapareho sa mga pamamaraan ng paglutas ng mga equation. Gayunpaman, malayo pa rin ang simbolismo ng Vieta modernong hitsura. Hindi niya nakilala ang mga negatibong numero, at samakatuwid, kapag nilulutas ang mga equation, isinasaalang-alang lamang niya ang mga kaso kung saan ang lahat ng mga ugat ay positibo.

2. Mga pamamaraan para sa paglutas ng mga quadratic equation

Ang mga quadratic equation ay ang pundasyon kung saan nakasalalay ang maringal na edipisyo ng algebra. Ang mga quadratic equation ay malawakang ginagamit sa paglutas ng trigonometriko, exponential, logarithmic, irrational at transendental equation at inequalities. Alam nating lahat kung paano lutasin ang mga quadratic equation mula sa paaralan (grade 8) hanggang sa graduation.

Sa kurso ng paaralan ng matematika, ang mga pormula ng mga ugat ng mga parisukat na equation ay pinag-aralan, sa tulong kung saan maaari mong malutas ang anumang mga parisukat na equation. Gayunpaman, may iba pang mga paraan upang malutas ang mga quadratic na equation na nagbibigay-daan sa iyo upang malutas ang maraming mga equation nang napakabilis at makatwiran. Mayroong sampung paraan upang malutas ang mga quadratic equation. Sa aking trabaho, sinuri ko ang bawat isa sa kanila nang detalyado.

1. PARAAN : Factorization ng kaliwang bahagi ng equation.

Solusyonan natin ang equation

X2 + 10x - 24 = 0.

I-factorize natin ang kaliwang bahagi:

X2 + 10x - 24 = x2 + 12x - 2x - 24 \u003d x (x + 12) - 2 (x + 12) \u003d (x + 12) (x - 2).

Samakatuwid, ang equation ay maaaring muling isulat bilang:

(x + 12)(x - 2) = 0

Dahil ang produkto ay zero, kung gayon ang isa sa mga kadahilanan nito ay zero. Samakatuwid, ang kaliwang bahagi ng equation ay naglalaho sa x = 2, pati na rin sa x = - 12. Nangangahulugan ito na ang numero 2 at - 12 ay ang mga ugat ng equation X2 + 10x - 24 = 0.

2. PARAAN : Buong parisukat na paraan ng pagpili.

Solusyonan natin ang equation X2 + 6x - 7 = 0.

Pumili tayo ng isang buong parisukat sa kaliwang bahagi.

Upang gawin ito, isinusulat namin ang expression na x2 + 6x sa sumusunod na form:

X2 + 6x = x2 + 2 x 3.

Sa resultang expression, ang unang termino ay ang parisukat ng numerong x, at ang pangalawa ay ang dobleng produkto ng x sa pamamagitan ng 3. Samakatuwid, upang makuha ang buong parisukat, kailangan mong magdagdag ng 32, dahil

x2 + 2 x 3 + 32 = (x + 3)2 .

Binabago namin ngayon ang kaliwang bahagi ng equation

X2 + 6x - 7 = 0,

pagdaragdag dito at pagbabawas ng 32. Mayroon tayong:

X2 + 6x - 7 = x2 + 2 x 3 + 32 - 3 2 - 7 = (x + 3)2 - 9 - 7 = (x + 3)2 - 16.

Kaya, ang equation na ito ay maaaring isulat bilang mga sumusunod:

(x + 3)2 - 16 = 0, (x + 3)2 = 16.

Kaya naman, x + 3 - 4 = 0, x1 = 1, o x + 3 = -4, x2 = -7.

3. PARAAN :Solusyon ng mga quadratic equation sa pamamagitan ng formula.

I-multiply ang magkabilang panig ng equation

Oh2 + bx + c = 0, a ≠ 0

sa 4a at magkakasunod na mayroon tayo:

4a2 X2 + 4abx + 4ac = 0,

((2ah)2 + 2 palakolb+ b2 ) - b2 + 4 ac= 0,

(2ax+b)2 = b2 - 4ac,

2ax + b = ± √ b2 - 4ac,

2ax = - b ± √ b2 - 4ac,

Mga halimbawa.

a) Lutasin natin ang equation: 4x2 + 7x + 3 = 0.

a = 4,b= 7, c = 3,D= b2 - 4 ac= 7 2 - 4 4 3 = 49 - 48 = 1,

D> 0, dalawa iba't ibang ugat;

Kaya, sa kaso ng isang positibong diskriminasyon, i.e. sa

b2 - 4 ac>0 , ang equation Oh2 + bx + c = 0 may dalawang magkaibang ugat.

b) Lutasin natin ang equation: 4x2 - 4x + 1 = 0,

a = 4,b= - 4, c = 1,D= b2 - 4 ac= (-4) 2 - 4 4 1= 16 - 16 = 0,

D= 0, isang ugat;

Kaya, kung ang discriminant ay zero, i.e. b2 - 4 ac= 0 , pagkatapos ay ang equation

Oh2 + bx + c = 0 may iisang ugat

sa) Lutasin natin ang equation: 2x2 + 3x + 4 = 0,

a = 2,b= 3, c = 4,D= b2 - 4 ac= 3 2 - 4 2 4 = 9 - 32 = - 13, D< 0.

pagpapatuloy
--PAGE_BREAK--

Ang equation na ito ay walang mga ugat.

Kaya, kung ang discriminant ay negatibo, i.e. b2 - 4 ac< 0 ,

ang equation Oh2 + bx + c = 0 walang ugat.

Formula (1) ng mga ugat ng quadratic equation Oh2 + bx + c = 0 nagbibigay-daan sa iyo upang mahanap ang mga ugat anuman quadratic equation (kung mayroon man), kabilang ang binawasan at hindi kumpleto. Ang pormula (1) ay ipinahayag sa salita tulad ng sumusunod: ang mga ugat ng isang quadratic equation ay katumbas ng isang fraction na ang numerator ay katumbas ng pangalawang coefficient, na kinuha gamit ang kabaligtaran na sign, kasama ang minus ang square root ng square ng coefficient na ito nang walang apat na beses ang produkto ng unang koepisyent ng libreng term, at ang denominator ay dalawang beses sa unang koepisyent.

4. PARAAN: Solusyon ng mga equation gamit ang Vieta's theorem.

Tulad ng nalalaman, ang ibinigay na quadratic equation ay may anyo

X2 + px+ c= 0. (1)

Ang mga ugat nito ay nagbibigay-kasiyahan sa Vieta theorem, na kung kailan a =1 may porma

/>x1 x2 = q,

x1 + x2 = - p

Mula dito maaari nating iguhit ang mga sumusunod na konklusyon (ang mga palatandaan ng mga ugat ay maaaring mahulaan mula sa mga coefficient p at q).

a) Kung ang termino ng buod q ng pinababang equation (1) ay positibo ( q> 0 ), pagkatapos ang equation ay may dalawang ugat ng parehong tanda at ito ang inggit ng pangalawang koepisyent p. Kung ang R< 0 , kung gayon ang parehong mga ugat ay negatibo kung R< 0 , pagkatapos ang parehong mga ugat ay positibo.

Halimbawa,

x2 – 3 x+ 2 = 0; x1 = 2 at x2 = 1, bilang q= 2 > 0 at p= - 3 < 0;

x2 + 8 x+ 7 = 0; x1 = - 7 at x2 = - 1, bilang q= 7 > 0 at p= 8 > 0.

b) Kung isang libreng miyembro q ng pinababang equation (1) ay negatibo ( q< 0 ), pagkatapos ang equation ay may dalawang ugat ng magkaibang tanda, at ang mas malaking ugat sa absolute value ay magiging positibo kung p< 0 , o negatibo kung p> 0 .

Halimbawa,

x2 + 4 x– 5 = 0; x1 = - 5 at x2 = 1, bilang q= - 5 < 0 at p= 4 > 0;

x2 – 8 x– 9 = 0; x1 = 9 at x2 = - 1, bilang q= - 9 < 0 at p= - 8 < 0.

5. PARAAN: Paglutas ng mga equation gamit ang "transfer" method.

Isaalang-alang ang quadratic equation

Oh2 + bx + c = 0, saan isang ≠ 0.

Ang pagpaparami ng parehong bahagi nito sa pamamagitan ng a, makuha natin ang equation

a2 X2 + abx + ac = 0.

Hayaan ah = y, saan x = y/a; pagkatapos ay dumating tayo sa equation

sa2 + sa pamamagitan ng+ ac = 0,

katumbas ng isang ito. mga ugat nito sa1 at sa 2 ay matatagpuan gamit ang Vieta's theorem.

Sa wakas nakuha namin

X1 = y1 /a at X1 = y2 /a.

Sa pamamaraang ito, ang koepisyent a ay pinarami ng libreng termino, na parang "itinapon" dito, samakatuwid ito ay tinatawag paraan ng paglipat. Ginagamit ang pamamaraang ito kapag madaling mahanap ang mga ugat ng isang equation gamit ang teorem ng Vieta at, higit sa lahat, kapag ang discriminant ay isang eksaktong parisukat.

Halimbawa.

Solusyonan natin ang equation 2x2 – 11x + 15 = 0.

Desisyon."Ilipat" natin ang koepisyent 2 sa libreng termino, bilang isang resulta makuha natin ang equation

sa2 – 11y + 30 = 0.

Ayon sa teorama ni Vieta

/>/>/>/>/>sa1 = 5 x1 = 5/2 x1 = 2,5

sa2 = 6 x2 = 6/2 x2 = 3.

Sagot: 2.5; 3.

6. PARAAN: Mga katangian ng mga coefficient ng isang quadratic equation.

PERO. Hayaan ang quadratic equation

Oh2 + bx + c = 0, saan isang ≠ 0.

1) Kung, a+b+ c = 0 (i.e. ang kabuuan ng mga coefficient ay zero), pagkatapos ay x1 = 1,

X2 = s/a.

Patunay. Hinahati namin ang magkabilang panig ng equation sa pamamagitan ng ≠ 0, nakukuha namin ang pinababang quadratic equation

x2 + b/ a x+ c/ a= 0.

/>Ayon sa teorama ni Vieta

x1 + x2 = - b/ a,

x1 x2 = 1 c/ a.

Sa pamamagitan ng kondisyon a-b+ c = 0, saan b= a + c. kaya,

/>x1 + x2 = - a+ b / a \u003d -1 - c / a,

x1 x2 = - 1 (-c/a),

mga. X1 = -1 at X2 = c/ a, na kailangan naming patunayan.

Mga halimbawa.

Solusyonan natin ang equation 345x2 - 137x - 208 = 0.

Desisyon. Bilang isang +b+ c \u003d 0 (345 - 137 - 208 \u003d 0), pagkatapos

X1 = 1, x2 = c/ a= -208/345.

Sagot: 1; -208/345.

2) Lutasin ang equation 132x2 – 247x + 115 = 0.

Desisyon. Bilang isang +b+ c \u003d 0 (132 - 247 + 115 \u003d 0), pagkatapos

X1 = 1, x2 = c/ a= 115/132.

Sagot: 1; 115/132.

B. Kung ang pangalawang koepisyent b= 2 k– kahit na numero, pagkatapos ay ang formula ng mga ugat

pagpapatuloy
--PAGE_BREAK--

Halimbawa.

Solusyonan natin ang equation 3x2 - 14x + 16 = 0.

Desisyon. Meron kami: a = 3,b= - 14, c = 16,k= - 7 ;

D= k2 – ac= (- 7) 2 – 3 16 = 49 – 48 = 1, D> 0, dalawang magkaibang ugat;

Sagot: 2; 8/3

AT. Pinababang Equation

X2 +px+q= 0

tumutugma sa pangkalahatang equation, kung saan a = 1, b= p at c =q. Samakatuwid, para sa pinababang quadratic equation, ang formula para sa mga ugat

kumuha ng form:

Ang formula (3) ay lalong madaling gamitin kapag R- kahit na numero.

Halimbawa. Solusyonan natin ang equation X2 – 14x – 15 = 0.

Desisyon. Meron kami: X1,2 =7±

Sagot: x1 = 15; X2 = -1.

7. PARAAN: Graphical na solusyon ng isang quadratic equation.

Kung sa equation

X2 + px+ q= 0

ilipat ang pangalawa at pangatlong termino sa kanang bahagi, nakukuha namin

X2 = - px- q.

Bumuo tayo ng mga graph ng dependence y \u003d x2 at y \u003d - px - q.

Ang graph ng unang dependence ay isang parabola na dumadaan sa pinanggalingan. Graph ng pangalawang dependency -

tuwid na linya (Larawan 1). Posible ang mga sumusunod na kaso:

Ang isang tuwid na linya at isang parabola ay maaaring mag-intersect sa dalawang punto, ang abscissas ng mga intersection point ay ang mga ugat ng isang quadratic equation;

Ang linya at ang parabola ay maaaring hawakan (isang karaniwang punto lamang), i.e. ang equation ay may isang solusyon;

Ang tuwid na linya at ang parabola ay walang mga karaniwang punto, i.e. ang isang quadratic equation ay walang mga ugat.

Mga halimbawa.

1) Lutasin natin ang equation sa graphical na paraan X2 - 3x - 4 = 0(Larawan 2).

Desisyon. Isinulat namin ang equation sa form X2 = 3x + 4.

Bumuo tayo ng parabola y = x2 at direktang y = 3x + 4. direkta

y = 3x + 4 maaaring itayo mula sa dalawang punto M (0; 4) at

N(3; 13) . Ang isang linya at isang parabola ay nagsalubong sa dalawang punto

PERO at AT may abscissa X1 = - 1 at X2 = 4 . Sagot : X1 = - 1;

X2 = 4.

2) Lutasin natin ang equation nang grapiko (Larawan 3) X2 - 2x + 1 = 0.

Desisyon. Isinulat namin ang equation sa form X2 = 2x - 1.

Bumuo tayo ng parabola y = x2 at direktang y = 2x - 1.

direkta y = 2x - 1 bumuo sa dalawang puntos M (0; - 1)

at N(1/2; 0) . Nagsalubong ang linya at parabola sa isang punto PERO kasama

abscissa x = 1. Sagot: x = 1.

3) Lutasin natin ang equation sa graphical na paraan X2 - 2x + 5 = 0(Larawan 4).

Desisyon. Isinulat namin ang equation sa form X2 = 5x - 5. Bumuo tayo ng parabola y = x2 at direktang y = 2x - 5. direkta y = 2x - 5 bumuo ng dalawang puntos M(0; - 5) at N(2.5; 0). Ang tuwid na linya at ang parabola ay walang mga intersection point, i.e. Ang equation na ito ay walang mga ugat.

Sagot. Ang equation X2 - 2x + 5 = 0 walang ugat.

8. PARAAN: Paglutas ng mga quadratic equation na may compass at straightedge.

Ang graphical na paraan upang malutas ang mga quadratic equation gamit ang isang parabola ay hindi maginhawa. Kung bumuo ka ng isang parabola point by point, pagkatapos ay nangangailangan ng maraming oras, at ang antas ng katumpakan ng mga resulta na nakuha ay mababa.

Iminumungkahi ko ang sumusunod na paraan para sa paghahanap ng mga ugat ng isang quadratic equation Oh2 + bx + c = 0 gamit ang isang compass at ruler (Larawan 5).

Ipagpalagay natin na ang nais na bilog ay nag-intersect sa axis

abscissa sa mga puntos B(x1 ; 0) at D(X2 ; 0), saan X1 at X2 - mga ugat ng equation Oh2 + bx + c = 0, at pumasa sa mga puntos

A(0; 1) at C(0;c/ a) sa y-axis. Pagkatapos, sa pamamagitan ng secant theorem, mayroon tayo OB OD= OA OC, saan OC= OB OD/ OA= x1 X2 / 1 = c/ a.

Ang gitna ng bilog ay nasa punto ng intersection ng mga patayo SF at SK, ibinalik sa mga midpoint ng chords AC at BD, Kaya naman

1) bumuo ng mga puntos (gitna ng bilog) at A(0; 1) ;

2) gumuhit ng bilog na may radius SA;

3) ang abscissas ng mga punto ng intersection ng bilog na ito sa axis Oh ay ang mga ugat ng orihinal na quadratic equation.

Sa kasong ito, tatlong mga kaso ang posible.

1) Ang radius ng bilog ay mas malaki kaysa sa ordinate ng sentro (AS> SK, oR> a+ c/2 a) , ang bilog ay nag-intersect sa x-axis sa dalawang punto (Larawan 6, a) B(x1 ; 0) at D(X2 ; 0) , saan X1 at X2 - mga ugat ng quadratic equation Oh2 + bx + c = 0.

2) Ang radius ng bilog ay katumbas ng ordinate ng sentro (AS= SB, oR= a+ c/2 a) , hinawakan ng bilog ang Ox axis (Fig. 6, b) sa punto B(x1 ; 0) , kung saan ang x1 ay ang ugat ng quadratic equation.

pagpapatuloy
--PAGE_BREAK--

3) Ang radius ng bilog ay mas mababa kaysa sa ordinate ng sentro, ang bilog ay walang mga karaniwang punto na may abscissa axis (Larawan 6, c), sa kasong ito ang equation ay walang solusyon.

Halimbawa.

Solusyonan natin ang equation X2 - 2x - 3 = 0(Larawan 7).

Desisyon. Tukuyin ang mga coordinate ng punto ng gitna ng bilog sa pamamagitan ng mga formula:

Gumuhit tayo ng bilog na radius SA, kung saan ang A (0; 1).

Sagot:X1 = - 1; X2 = 3.

9. PARAAN: Paglutas ng mga quadratic equation gamit ang isang nomogram.

Ito ay isang luma at hindi nararapat na nakalimutang pamamaraan para sa paglutas ng mga quadratic equation, na inilagay sa p. 83 (tingnan ang Bradis V.M. Four-digit mathematical tables. - M., Enlightenment, 1990).

Talahanayan XXII. Nomogram para sa Paglutas ng Equation z2 + pz+ q= 0 . Binibigyang-daan ng nomogram na ito, nang hindi nilulutas ang quadratic equation, na matukoy ang mga ugat ng equation sa pamamagitan ng mga coefficient nito.

Ang curvilinear scale ng nomogram ay binuo ayon sa mga formula (Larawan 11):

Ipagpalagay OS = p,ED= q, OE = a(lahat sa cm), mula sa pagkakatulad ng mga tatsulok SAN at CDF nakukuha natin ang proporsyon

kung saan, pagkatapos ng mga pagpapalit at pagpapagaan, ang equation ay sumusunod

z2 + pz+ q= 0,

at ang sulat z nangangahulugang ang label ng anumang punto sa curved scale.

Mga halimbawa.

1) Para sa equation z2 - 9 z+ 8 = 0 ang nomogram ay nagbibigay ng mga ugat

z1 = 8,0 at z2 = 1,0 (Larawan 12).

2) Malutas namin ang equation gamit ang nomogram

2 z2 - 9 z+ 2 = 0.

Hinahati namin ang mga coefficient ng equation na ito sa pamamagitan ng 2, nakuha namin ang equation

z2 - 4,5 z+ 1 = 0.

Ang Nomogram ay nagbibigay ng mga ugat z1 = 4 at z2 = 0,5.

3) Para sa equation

z2 - 25 z+ 66 = 0

Ang mga coefficients p at q ay wala sa sukat, gagawin namin ang pagpapalit z= 5 t, nakukuha namin ang equation

t2 - 5 t+ 2,64 = 0,

na aming nilulutas sa pamamagitan ng isang nomogram at nakukuha t1 = 0,6 at t2 = 4,4, saan z1 = 5 t1 = 3,0 at z2 = 5 t2 = 22,0.

10. PARAAN: Geometric na paraan ng paglutas ng mga quadratic equation.

Noong sinaunang panahon, kapag ang geometry ay mas binuo kaysa sa algebra, ang mga quadratic equation ay nalutas hindi sa algebraically, ngunit sa geometrically. Magbibigay ako ng isang halimbawa na naging tanyag mula sa "Algebra" ng al-Khwarizmi.

Mga halimbawa.

1) Lutasin ang equation X2 + 10x = 39.

Sa orihinal, ang problemang ito ay nabuo tulad ng sumusunod: "Ang parisukat at sampung ugat ay katumbas ng 39" (Larawan 15).

Desisyon. Isaalang-alang ang isang parisukat na may gilid na x, ang mga parihaba ay itinayo sa mga gilid nito upang ang kabilang panig ng bawat isa sa kanila ay 2.5, samakatuwid, ang lugar ng beach ay 2.5x. Ang resultang figure ay pagkatapos ay pupunan sa isang bagong parisukat ABCD, pagkumpleto ng apat na pantay na mga parisukat sa mga sulok, ang gilid ng bawat isa sa kanila ay 2.5, at ang lugar ay 6.25.

parisukat S parisukat A B C D ay maaaring katawanin bilang kabuuan ng mga lugar: ang orihinal na parisukat X2 , apat na parihaba (4 2.5x = 10x) at apat na nakadikit na parisukat (6,25 4 = 25) , ibig sabihin. S= X2 + 10x + 25. Pinapalitan

X2 + 10x numero 39 , naiintindihan namin iyon S= 39 + 25 = 64 , kung saan ito ay sumusunod na ang gilid ng parisukat A B C D, ibig sabihin. segment ng linya AB = 8. Para sa nais na panig X ang orihinal na parisukat na nakukuha natin

2) Ngunit, halimbawa, kung paano nalutas ng mga sinaunang Griyego ang equation sa2 + 6y - 16 = 0.

Desisyon ipinapakita sa fig. 16, kung saan

sa2 + 6y = 16, o y2 + 6y + 9 = 16 + 9.

Desisyon. Mga ekspresyon sa2 + 6y + 9 at 16 + 9 geometrically kumakatawan sa parehong parisukat, at ang orihinal na equation sa2 + 6y - 16 + 9 - 9 = 0 ay ang parehong equation. Saan natin nakukuha yan y + 3 = ± 5, o sa1 = 2, y2 = - 8 (Larawan 16).

3) Lutasin ang geometric equation sa2 - 6y - 16 = 0.

Pagbabago ng equation, nakukuha namin

sa2 - 6y = 16.

Sa fig. 17 hanapin ang "mga imahe" ng expression sa2 - 6u, mga. mula sa lugar ng isang parisukat na may gilid y ibawas ng dalawang beses ang lugar ng isang parisukat na may gilid na katumbas ng 3 . Kaya, kung ang expression sa2 - 6y idagdag 9 , pagkatapos ay makuha namin ang lugar ng isang parisukat na may gilid y - 3. Pinapalitan ang ekspresyon sa2 - 6y katumbas nitong numero 16,

makuha namin: (y - 3)2 = 16 + 9, mga. y - 3 = ± √25, o y - 3 = ± 5, kung saan sa1 = 8 at sa2 = - 2.

Konklusyon

Ang mga quadratic equation ay malawakang ginagamit sa paglutas ng trigonometriko, exponential, logarithmic, irrational at transendental equation at inequalities.

Gayunpaman, ang halaga ng mga quadratic equation ay hindi lamang nakasalalay sa kagandahan at kaiklian ng paglutas ng mga problema, bagama't ito ay napakahalaga. Hindi gaanong mahalaga ang katotohanan na bilang isang resulta ng paggamit ng mga quadratic equation sa paglutas ng mga problema, ang mga bagong detalye ay madalas na natuklasan, ang mga kagiliw-giliw na generalization ay maaaring gawin at mga pagpipino, na sinenyasan ng isang pagsusuri ng mga nakuha na mga formula at relasyon.

Nais ko ring tandaan na ang paksang ipinakita sa gawaing ito ay hindi pa rin gaanong pinag-aralan, hindi nila ito hinarap, samakatuwid ito ay puno ng maraming nakatago at hindi alam, na nagbibigay ng isang mahusay na pagkakataon para sa mga iba pang gawain sa itaas niya.

Dito ko naayos ang tanong ng paglutas ng mga quadratic equation, at ano,

kung may iba pang mga paraan upang malutas ang mga ito?! Muli, maghanap ng magagandang pattern, ilang katotohanan, paglilinaw, gumawa ng mga generalization, tuklasin ang lahat ng bago at bago. Ngunit ito ay mga katanungan para sa mga gawain sa hinaharap.

Summing up, maaari nating tapusin: ang mga quadratic equation ay may malaking papel sa pag-unlad ng matematika. Alam nating lahat kung paano lutasin ang mga quadratic equation mula sa paaralan (grade 8) hanggang sa graduation. Ang kaalamang ito ay maaaring maging kapaki-pakinabang sa atin sa buong buhay.

Dahil ang mga pamamaraang ito para sa paglutas ng mga quadratic equation ay madaling gamitin, tiyak na dapat itong maging interesado sa mga mag-aaral na mahilig sa matematika. Ginagawang posible ng aking trabaho na tingnan ang ibang mga problema na itinakda ng matematika sa harap natin.

Panitikan:

1. Alimov Sh.A., Ilyin V.A. et al. Algebra, 6-8. Trial textbook para sa 6-8 grade high school. - M., Edukasyon, 1981.

2. Bradis V.M. Apat na digit na mathematical table para sa high school. Ed. ika-57. - M., Edukasyon, 1990. S. 83.

3. Kruzhepov A.K., Rubanov A.T. Problema ng libro sa algebra at elementarya function. Textbook para sa pangalawang dalubhasang institusyong pang-edukasyon. - M., mas mataas na paaralan, 1969.

4. Okunev A.K. Quadratic function, equation at hindi pagkakapantay-pantay. Isang gabay para sa guro. - M., Edukasyon, 1972.

5. Presman A.A. Paglutas ng isang quadratic equation na may compass at straightedge. - M., Kvant, No. 4/72. S. 34.

6. Solomnik V.S., Milov P.I. Koleksyon ng mga tanong at gawain sa matematika. Ed. - Ika-4, idagdag. - M., Mas Mataas na Paaralan, 1973.

7. Khudobin A.I. Koleksyon ng mga problema sa algebra at elementary functions. Isang gabay para sa guro. Ed. ika-2. - M., Edukasyon, 1970.

https://pandia.ru/text/78/082/images/image002_237.gif" height="952"> MOU "Sergievskaya Secondary School"

Nakumpleto ni: Sizikov Stanislav

Guro:

kasama. Sergievka, 2007

1. Panimula. Mga Quadratic Equation sa Sinaunang Babylon…………………….3

2. Mga parisukat na equation sa Diaphant…………..……………………………….4

3. Quadratic equation sa India ……………………………………………………………………………………………………………………… …………………………………………………………………

4. Quadratic equation sa al-Khorezmi …………………………………..6

5. Mga parisukat na equation sa Europe XIII - XYII…………………………………7

6. Tungkol sa Vieta theorem …………………………………………………………………..9

7. Sampung paraan upang malutas ang mga quadratic equation……………………..10

8. Konklusyon …………………………………………………………………20

9. Mga Sanggunian ………………………………………………………21

Panimula

Quadratic equation

Ang mga quadratic equation ay ang pundasyon kung saan nakasalalay ang maringal na edipisyo ng algebra. Ang mga quadratic equation ay malawakang ginagamit sa paglutas ng trigonometric, exponential, logarithmic, hindi makatwirang equation. Alam nating lahat kung paano lutasin ang mga quadratic equation, simula sa grade 8. Ngunit paano nagmula at umunlad ang kasaysayan ng paglutas ng mga quadratic equation?

Mga Quadratic Equation sa Sinaunang Babylon

Ang pangangailangan upang malutas ang mga equation hindi lamang ng una, kundi pati na rin ng ikalawang antas, pabalik sa unang panahon, ay sanhi ng pangangailangan upang malutas ang mga problema na may kaugnayan sa paghahanap ng mga lugar ng lupa; mga gawaing lupa na may likas na militar, gayundin sa pag-unlad ng astronomiya at matematika mismo. Ang mga quadratic equation ay nagawang malutas ang mga 2000 BC. e. Babylonians. Gamit ang modernong algebraic notation, maaari nating sabihin na sa kanilang mga cuneiform na teksto ay mayroong, bilang karagdagan sa mga hindi kumpleto, tulad, halimbawa, kumpletong quadratic equation: x2 + x = , : x2 - x = 14https://pandia.ru/text /78/082 /images/image005_150.gif" width="16" height="41 src=">)2 + 12 = x; Sumulat si Bhaskara sa ilalim ng balatkayo

x2- 64X = - 768

at, upang makumpleto ang kaliwang bahagi ng equation na ito sa parisukat, idinagdag niya ang 322 sa magkabilang panig, at pagkatapos ay: x2- 64x + 322 = - 768 + 1024;

(X- 32)2 = 256; X - 32 = ± 16, xt = 16, hg= 48.

Quadratic equation sa al - Khorezmi

Ang algebraic treatise ni Al-Khwarizmi ay nagbibigay ng klasipikasyon ng linear at quadratic equation. Ang may-akda ay naglista ng 6 na uri ng mga equation, na nagpapahayag ng mga ito bilang mga sumusunod:

1) "Ang mga parisukat ay katumbas ng mga ugat", i.e. ax2 = sa.

2) "Ang mga parisukat ay katumbas ng numero", i.e. ah2= kasama.

3) "Ang mga ugat ay katumbas ng bilang", i.e. ah = s.

4) "Ang mga parisukat at numero ay katumbas ng mga ugat", i.e. ah2+ c = sa.

5) "Ang mga parisukat at ugat ay katumbas ng bilang", i.e. ah2+ sa = s.

6) "Ang mga ugat at numero ay katumbas ng mga parisukat", i.e. sa+ c \u003d ax2. Para kay al-Khwarizmi, na umiwas sa paggamit ng mga negatibong numero, ang mga tuntunin ng bawat isa sa mga equation na ito ay mga addend, hindi mga pagbabawas. Sa kasong ito, ang mga equation na walang positibong solusyon ay malinaw na hindi isinasaalang-alang. Nagtakda ang may-akda ng mga pamamaraan para sa paglutas ng mga equation na ito. Ang kanyang desisyon, siyempre, ay hindi ganap na tumutugma sa atin. Hindi sa banggitin ang katotohanan na ito ay purong retorika, dapat tandaan, halimbawa, na kapag nilutas ang isang hindi kumpletong quadratic equation ng unang uri, ang al-Khwarizmi, tulad ng lahat ng mga mathematician bago ang ika-17 siglo, ay hindi isinasaalang-alang ang zero. solusyon, marahil dahil sa mga partikular na praktikal na gawain, hindi ito mahalaga. Kapag nilulutas ang kumpletong quadratic equation, itinakda ni al-Khorezmi ang mga patakaran para sa paglutas ng mga ito gamit ang mga partikular na halimbawang numero, at pagkatapos ang kanilang mga geometric na patunay.

Kumuha tayo ng isang halimbawa.

Suliranin 14. “Ang parisukat at ang bilang 21 ay katumbas ng 10 ugat. Hanapin ang ugat "(ibig sabihin ang ugat ng equation x2+ 21 = 10X).

Ang solusyon ng may-akda ay ganito: hatiin ang bilang ng mga ugat sa kalahati, makakakuha ka ng 5, i-multiply ang 5 sa sarili nito, ibawas ang 21 sa produkto, 4 ang natitira. Kunin ang ugat ng 4, makakakuha ka ng 2. Ibawas ang 2 sa 5, ikaw makakuha ng 3, ito ang magiging ninanais na ugat. O magdagdag ng 2 hanggang 5, na magbibigay ng 7, ito ay ugat din.

Ang treatise ng al-Khwarizmi ay ang unang libro na dumating sa amin, kung saan ang pag-uuri ng mga quadratic equation ay sistematikong ipinakita at ang mga formula para sa kanilang solusyon ay ibinigay.

Quadratic equation sa EuropeXIII- XVIImga siglo

Ang mga pormula para sa paglutas ng mga parisukat na equation sa modelo ng al-Khwarizmi sa Europa ay unang itinakda sa Aklat ng Abacus (nailathala sa Roma noong kalagitnaan ng huling siglo, ang Fibonacci Book of the Abacus ay naglalaman ng 459 na pahina), na nakasulat sa 1202 ng Italian mathematician na si Leonardo Fibonacci. Ang napakalaking gawaing ito, na sumasalamin sa impluwensya ng matematika mula sa parehong mga bansa ng Islam at Sinaunang Greece, ay nakikilala sa pamamagitan ng parehong pagkakumpleto at kalinawan ng presentasyon. Ang may-akda ay nakapag-iisa na bumuo ng ilang mga bagong algebraic na halimbawa ng paglutas ng problema at ang una sa Lumapit ang Europa sa pagpapakilala ng mga negatibong numero. Ang kanyang libro ay nag-ambag sa paglaganap ng algebraic na kaalaman hindi lamang sa Italya, kundi pati na rin sa Alemanya, Pransya at iba pang mga bansa sa Europa. Maraming mga gawain mula sa Aklat ng Abacus ang pumasa sa halos lahat ng mga aklat-aralin sa Europa noong ika-16-17 siglo. at bahagyang XVIII.

Pangkalahatang tuntunin para sa paglutas ng mga quadratic na equation ay binawasan sa isang solong canonical form x2+ sa = s, para sa lahat ng posibleng kumbinasyon ng mga palatandaan ng mga coefficient kasama dito ay nabuo sa Europa lamang noong 1544. M. Stiefel.

Ang Vieta ay may pangkalahatang derivation ng formula para sa paglutas ng isang quadratic equation, ngunit ang Vieta ay kumikilala lamang ng mga positibong ugat. Ang mga Italian mathematician na sina Tartaglia, Cardaco, Bombelli ay kabilang sa mga una noong ika-16 na siglo. isaalang-alang, bilang karagdagan sa positibo, at negatibong mga ugat. Lamang sa siglo XVII. salamat sa mga gawa ni Girard, Descartes, Newton at iba pang mga siyentipiko, ang paraan ng paglutas ng mga quadratic equation ay tumatagal sa isang modernong anyo.

Tungkol sa teorama ni Vieta

Ang theorem na nagpapahayag ng relasyon sa pagitan ng mga coefficient ng isang quadratic equation at ang mga ugat nito, na may pangalang Vieta, ay binuo niya sa unang pagkakataon noong 1591 bilang mga sumusunod: "Kung AT+ D, pinarami ng PERO minus A2, katumbas BD, pagkatapos PERO katumbas AT at pantay D».

Upang maunawaan ang Vieta, dapat tandaan iyon PERO, tulad ng anumang
patinig, para sa kanya ay hindi kilala (aming X), mga patinig
SA,D- mga coefficient para sa hindi alam. Sa wika ng modernong algebra, ang pormulasyon ni Vieta sa itaas ay nangangahulugang: kung

(a+ c) x - x 2 = ab, x2 - (a+ b) x + ab = 0, x1 = a, x2 = b.

Sa pagpapahayag ng ugnayan sa pagitan ng mga ugat at coefficient ng mga equation sa pamamagitan ng mga pangkalahatang formula na isinulat gamit ang mga simbolo, itinatag ng Viet ang pagkakapareho sa mga paraan ng paglutas ng mga equation. Gayunpaman, ang simbolismo ng Vieta ay malayo pa rin sa modernong anyo nito. Hindi niya nakilala ang mga negatibong numero at samakatuwid, sa paglutas ng mga equation, isinasaalang-alang lamang niya ang mga kaso kung saan ang lahat ng mga ugat ay positibo.

Sampung Paraan para Malutas ang Mga Quadratic Equation

Sa kurso ng paaralan ng matematika, ang mga pormula ng mga ugat ng mga parisukat na equation ay pinag-aralan, sa tulong kung saan maaari mong malutas ang anumang mga parisukat na equation. Gayunpaman, may iba pang mga paraan upang malutas ang mga quadratic na equation na nagbibigay-daan sa iyo upang malutas ang maraming mga equation nang napakabilis at makatwiran. Mayroong sampung paraan upang malutas ang mga quadratic equation. Isaalang-alang natin ang bawat isa sa kanila.

1. Factorization ng kaliwang bahagi ng equation

Solusyonan natin ang equation x2+ 10X- 24 = 0. I-factorize natin ang kaliwang bahagi ng equation:

x2 + 10x - 24 = x2 + 12x - 2x - 24 =

X(x + x + 12) = (x + 12)(x - 2).

Samakatuwid, ang equation ay maaaring muling isulat bilang:

( X + 12)(x - 2) = 0.

Dahil ang produkto ay zero, kahit isa sa mga salik nito ay zero. Samakatuwid, ang kaliwang bahagi ng equation ay naglalaho kapag x = 2, pati na rin X= - 12. Nangangahulugan ito na ang mga numero 2 at - 12 ay ang mga ugat ng equation na x2 + 10x - 24 = 0.

2. Buong parisukat na paraan ng pagpili

Ipaliwanag natin ang pamamaraang ito gamit ang isang halimbawa.

Lutasin natin ang equation na x2 + 6x - 7 = 0. Pumili ng isang buong parisukat sa kaliwang bahagi. Upang gawin ito, isinusulat namin ang expression na x2 + 6x sa sumusunod na form:

x2 + 6x = x2 + 2*x*3.

Sa resultang expression, ang unang termino ay ang parisukat ng numerong x, at ang pangalawa ay ang dobleng produkto ng x sa pamamagitan ng 3. Samakatuwid, upang makuha ang buong parisukat, kailangan mong magdagdag ng 32, dahil

x2 + 2 x 3 + 32 = (x + 3)2.

Binabago namin ngayon ang kaliwang bahagi ng equation

x2 + 6x - 7 = 0,

pagdaragdag dito at pagbabawas ng 32. Mayroon tayong:

x2 + 6x - 7 = x2 + 2 X 3 +– 7 = (X- \u003d (x - Z) 2 - 16 .

Kaya, ang equation na ito ay maaaring isulat bilang mga sumusunod:

(x + = 0, ibig sabihin. (x + 3)2 = 16.

Kaya naman, X+ 3 \u003d 4 x1 \u003d 1, o x + 3 \u003d - 4, x2 \u003d - 7.

3. Solusyon ng mga quadratic equation sa pamamagitan ng formula

I-multiply ang magkabilang panig ng equation

ah2+ sa+ c = 0, isang ≠ 0, sa 4a at sunod-sunod na mayroon tayo:

4a2 x2 + 4abx+ 4ac = 0,

((2ax)2 + 2 axb + b2 ) - b2 + 4ac= 0,

(2ax +b)2 = in2- 4ac,

2ax+ b= ± https://pandia.ru/text/78/082/images/image006_128.gif" width="71" height="27">, x1,2 =

Sa kaso ng isang positibong diskriminasyon, ibig sabihin, sa v2 - 4ac > 0, equation ah2+ sa + s Ang = 0 ay may dalawang magkaibang ugat.

Kung zero ang discriminant, i.e. v2 - 4ac = 0, pagkatapos ay ang equation ah2+ sa+ kasama Ang = 0 ay may iisang ugat, x = - https://pandia.ru/text/78/082/images/image009_95.gif" width="14" height="62"> Ang mga ugat nito ay nakakatugon sa Vieta theorem, na, kailan a= 1 ang may anyo

x1 x2 = q,

x1 + x2 = - R.

Mula dito maaari nating iguhit ang mga sumusunod na konklusyon (sa pamamagitan ng mga coefficient R at q mahuhulaan ang mga palatandaan ng ugat).

a) Kung isang libreng miyembro q pinababang equation (1)
positibo (q> 0), kung gayon ang equation ay may dalawang magkapareho
sa pamamagitan ng tanda ng ugat at ito ay nakasalalay sa pangalawang koepisyent R
Kung ang R> 0, kung gayon ang parehong mga ugat ay negatibo kung R< 0, tapos pareho
Ang mga ugat ay positibo.

Halimbawa,

x2- 3X + 2 = 0; x1= 2 at x2 = 1, dahil q = 2 > 0 u p = - 3 < 0;

x2 + 8x + 7 = 0; x 1 \u003d - 7 at x2 \u003d - 1, mula noon q= 7 > 0 at R = 8 > 0.

b) Kung isang libreng miyembro q pinababang equation (1)
negatibo (q < 0), kung gayon ang equation ay may dalawang ugat ng magkaibang tanda, at ang mas malaking ugat sa ganap na halaga ay magiging positibo kung R< 0, o negatibo kung p > 0.

Halimbawa,

x2 + 4x - 5 = 0; x1 \u003d - 5 at x2 \u003d 1, dahil q = - 5 < 0 и R= 4 > 0;

x2 - 8x - 9 = 0; x1 = 9 at x2= - 1 kasi q = - 9 < и R= - 8 < 0.

5. Solusyon ng mga equation sa pamamagitan ng paraan ng "transfer"

Isaalang-alang ang quadratic equation ax2 + in+ c = 0, saan isang ≠ 0. Pagpaparami ng magkabilang bahagi nito sa pamamagitan ng a, makuha namin ang equation a2x2 +abx+ ac= 0.

Hayaan ah = y saan X=; pagkatapos ay dumating tayo sa equation

y2+ sa pamamagitan ng+ ac = 0,

katumbas ng isang ito. mga ugat nito y1 at y2 hanapin sa tulong ng teorama ni Vieta. Sa wakas nakuha namin x1= https://pandia.ru/text/78/082/images/image012_77.gif" width="24" height="43">.

Sa pamamaraang ito, ang koepisyent a ay pinarami ng libreng termino, na parang "itinapon" dito, kung kaya't ito ay tinawag paraan ng paglipat. Ginagamit ang pamamaraang ito kapag madaling mahanap ang mga ugat ng isang equation gamit ang teorem ng Vieta at, higit sa lahat, kapag ang discriminant ay isang eksaktong parisukat.

1. Lutasin ang equation na 2x2 - 11x + 15 = 0.

Desisyon."Ilipat" natin ang koepisyent 2 sa libreng termino, bilang isang resulta makuha natin ang equation

y2 - 11 sa+ 30 = 0.

Ayon sa Vieta theorem, y1 = 5, y2 = 6, kaya x1 = https://pandia.ru/text/78/082/images/image014_69.gif" width="16 height=41" height="41" >, t e.

x1 = 2.5 x2 = 3.

Sagot: 2,5; 3.

6. Mga katangian ng mga coefficient ng parisukatmga equation

A. Hayaang magbigay ng quadratic equation

ax2 + sa + c= 0, kung saan a ≠ 0.

1. Kung ang isang + sa + kasama= 0 (ibig sabihin, ang kabuuan ng mga coefficient ng equation ay katumbas ng zero), pagkatapos x1 = 1, x2 = .

2. Kung a - b + c= 0, ob = a + c, pagkatapos x1 = - 1, X 2 = - https://pandia.ru/text/78/082/images/image016_58.gif" width="44 height=41" height="41">.

Sagot: 1; 184">

Posible ang mga sumusunod na kaso:

Ang isang tuwid na linya at isang parabola ay maaaring mag-intersect sa dalawang punto, ang abscissas ng mga intersection point ay ang mga ugat ng isang quadratic equation;

Ang isang tuwid na linya at isang parabola ay maaaring hawakan (isang karaniwang punto lamang), iyon ay, ang equation ay may isang solusyon;

Ang tuwid na linya at ang parabola ay walang mga karaniwang puntos, iyon ay, ang quadratic equation ay walang mga ugat.

Mga halimbawa.

1. Grapikong lutasin natin ang equation na x2 - 3x - 4 = 0 (Larawan 2).

Desisyon. Isinulat namin ang equation sa form x2 = 3x + 4.

Bumuo tayo ng parabola y = x2 at direktang y= 3x + 4. Direkta sa= 3x + 4 ay maaaring itayo mula sa dalawang puntos na M(0; 4) at N(3; 13). Ang isang linya at isang parabola ay nagsalubong sa dalawang punto A hanggang B may abscissa x1= - 1 at x2 = 4.

Sagot: x1= - 1, x, = 4.

8. Paglutas ng mga quadratic equation na may compass at straightedge

Ang graphical na paraan upang malutas ang mga quadratic equation gamit ang isang parabola ay hindi maginhawa. Kung bumuo ka ng isang parabola point by point, pagkatapos ay nangangailangan ng maraming oras, at ang antas ng katumpakan ng mga resulta na nakuha ay mababa.

Iminumungkahi namin ang sumusunod na pamamaraan para sa paghahanap ng mga ugat ng isang quadratic equation

ah2+ sa+ kasama= 0

gamit ang isang compass at ruler (Fig.).

Ipagpalagay natin na ang nais na bilog ay nagsalubong sa abscissa axis sa mga punto B(x1; 0) at D(x2 ; 0), saan x1 at x2- mga ugat ng equation ax2 + in+kasama=0,
at dumadaan sa mga puntong A(0; 1) at C(0; ) sa y-axis..gif" width="197" height="123">

Kaya: 1) bumuo ng mga puntos https://pandia.ru/text/78/082/images/image023_40.gif" width="171" height="45"> ang bilog ay nag-intersect sa OX axis sa punto B(x1;0 ), at D(x1 ; 0), kung saan ang x1 at x2 - mga ugat ng quadratic equation ax2+bx+c = 0.

2) Ang radius ng bilog ay katumbas ng ordinate ng sentro , hinawakan ng bilog ang x-axis sa puntong B(x1; 0), kung saan xx ay ang ugat ng quadratic equation.

3) Ang radius ng bilog ay mas mababa sa ordinate ng gitnang kaliwa">

https://pandia.ru/text/78/082/images/image029_34.gif" width="612" height="372">40" height="14">

https://pandia.ru/text/78/082/images/image031_28.gif" width="612" height="432 src=">

Saan pagkatapos ng mga pagpapalit at

pagpapasimple, ang equation na z2+pz+q=0 ay sumusunod, at ang letrang z ay nangangahulugan ng label ng anumang punto ng curvilinear scale.

10. Geometric na pamamaraan para sa paglutas ng mga quadratic equation

Noong sinaunang panahon, kapag ang geometry ay mas binuo kaysa sa algebra, ang mga quadratic equation ay nalutas hindi sa algebraically, ngunit sa geometrically. Magbigay tayo ng isang halimbawa na naging tanyag mula sa Algebra ni al-Khwarizmi.

At apat na nakadugtong na mga parisukat i.e. S=x2+10x+25. Ang pagpapalit ng x2+10x ng 39, makuha natin ang S = 39 + 25 = 64, na nangangahulugan na ang gilid ng parisukat A B C D, ibig sabihin, segment AB= 8. Para sa kinakailangang panig X ang orihinal na parisukat na nakukuha natin

Konklusyon

Alam nating lahat kung paano lutasin ang mga quadratic equation, mula sa paaralan hanggang sa pagtatapos. Ngunit sa kurso ng paaralan ng matematika, ang mga pormula ng mga ugat ng mga parisukat na equation ay pinag-aralan, sa tulong kung saan ang anumang mga parisukat na equation ay maaaring malutas. Gayunpaman, nang mas malalim na pag-aralan ang isyung ito, naging kumbinsido ako na may iba pang mga paraan upang malutas ang mga quadratic equation na nagbibigay-daan sa iyo upang malutas ang maraming mga equation nang napakabilis at makatwiran.

Siguro ang matematika ay nasa isang lugar sa ibang mga sukat, hindi nakikita ng mata - lahat ay nakasulat at nakuha lang natin ang lahat ng mga bagong katotohanan mula sa butas ng mga mundo? ... Alam ng Diyos; ngunit lumalabas na kung ang mga physicist, chemist, economist o archaeologist ay nangangailangan ng isang bagong modelo ng istraktura ng mundo, ang modelong ito ay maaaring palaging kunin mula sa istante kung saan inilagay ito ng mga mathematician tatlong daang taon na ang nakalilipas, o tipunin mula sa mga bahaging nakahiga sa parehong istante. Marahil ang mga bahaging ito ay kailangang baluktot, iakma sa isa't isa, pinakintab, mabilis na makinang ng ilang bagong teorem bushings; ngunit ang teorya ng resulta ay hindi lamang maglalarawan sa aktwal na sitwasyon na lumitaw, ngunit hinuhulaan din ang mga kahihinatnan! ...

Ang isang kakaibang bagay ay ang larong ito ng isip, na laging tama ...

Panitikan

1. Alimov SHA., Ilyin VA. et al. Algebra, 6-8. Teksbuk ng pagsubok para sa 6-8 na baitang ng mataas na paaralan. - M., Edukasyon, 1981.

2.Bradis math table para sa high school. Ed. ika-57. - M., Edukasyon, 1990. S. 83.

3. Zlotsky - mga gawain sa pagtuturo ng matematika. Ang libro para sa guro. - M., Edukasyon, 1992.

4.M., Mathematics (dagdag sa pahayagang "Una ng Setyembre"), Blg. 21/96, 10/97, 24/97, 18/98, 21/98.

5. Okunev function, equation at hindi pagkakapantay-pantay. Isang gabay para sa guro. - M., Edukasyon, 1972.

6. Solomnik B. C., Matamis na tanong at problema sa matematika. Ed. Ika-4, idagdag. - M., Mas Mataas na Paaralan, 1973.

7.M., Mathematics (dagdag sa pahayagang "Una ng Setyembre"), Blg. 40, 2000.

Pagsusuri

para sa gawain ng isang mag-aaral ng ika-11 baitang ng MOU "Sergievskaya pangalawang

komprehensibong paaralan"

Sa kurso ng paaralan ng matematika, ang mga pormula ng mga ugat ng mga parisukat na equation ay pinag-aralan, sa tulong kung saan maaari mong malutas ang anumang mga parisukat na equation. Gayunpaman, may iba pang mga paraan upang malutas ang mga quadratic na equation na nagbibigay-daan sa iyo upang malutas ang maraming mga equation nang napakabilis at makatwiran. Mayroong sampung paraan upang malutas ang mga quadratic equation. Sa aking trabaho, sinuri ko ang bawat isa sa kanila nang detalyado.

1. PARAAN : Factorization ng kaliwang bahagi ng equation.

Solusyonan natin ang equation

x 2 + 10x - 24 = 0.

I-factorize natin ang kaliwang bahagi:

x 2 + 10x - 24 \u003d x 2 + 12x - 2x - 24 \u003d x (x + 12) - 2 (x + 12) \u003d (x + 12) (x - 2).

Samakatuwid, ang equation ay maaaring muling isulat bilang:

(x + 12)(x - 2) = 0

Dahil ang produkto ay zero, kung gayon ang isa sa mga kadahilanan nito ay zero. Samakatuwid, ang kaliwang bahagi ng equation ay naglalaho sa x = 2, pati na rin sa x = - 12. Nangangahulugan ito na ang numero 2 at - 12 ay ang mga ugat ng equation x 2 + 10x - 24 = 0.

2. PARAAN : Buong parisukat na paraan ng pagpili.

Solusyonan natin ang equation x 2 + 6x - 7 = 0.

Pumili tayo ng isang buong parisukat sa kaliwang bahagi.

Upang gawin ito, isinusulat namin ang expression na x 2 + 6x sa sumusunod na anyo:

x 2 + 6x = x 2 + 2 x 3.

Sa resultang expression, ang unang termino ay ang parisukat ng numerong x, at ang pangalawa ay ang dobleng produkto ng x sa pamamagitan ng 3. Samakatuwid, upang makuha ang buong parisukat, kailangan mong magdagdag ng 3 2, dahil

x 2+ 2 x 3 + 3 2 \u003d (x + 3) 2.

Binabago namin ngayon ang kaliwang bahagi ng equation

x 2 + 6x - 7 = 0,

pagdaragdag dito at pagbabawas ng 3 2 . Meron kami:

x 2 + 6x - 7 = x 2+ 2 x 3 + 3 2 - 3 2 - 7 = (x + 3) 2 - 9 - 7 = (x + 3) 2 - 16.

Kaya, ang equation na ito ay maaaring isulat bilang mga sumusunod:

(x + 3) 2 - 16 = 0, (x + 3) 2 = 16.

Kaya naman, x + 3 - 4 = 0, x 1 = 1, o x + 3 = -4, x 2 = -7.

3. PARAAN :Solusyon ng mga quadratic equation sa pamamagitan ng formula.

I-multiply ang magkabilang panig ng equation

ah 2+bx + c = 0, a ≠ 0

sa 4a at magkakasunod na mayroon tayo:

4a 2 x 2 + 4abx + 4ac = 0,

((2ax) 2 + 2axb + b 2 ) - b 2 + 4 ac = 0,

(2ax + b) 2 = b 2 - 4ac,

2ax + b \u003d ± √ b 2 - 4ac,

2ax \u003d - b ± √ b 2 - 4ac,

Mga halimbawa.

a) Lutasin natin ang equation: 4x2 + 7x + 3 = 0.

a = 4,b= 7, c = 3,D = b 2 - 4 ac = 7 2 - 4 4 3 = 49 - 48 = 1,

D > 0, dalawang magkaibang ugat;

Kaya, sa kaso ng isang positibong diskriminasyon, i.e. sa

b 2 - 4 ac >0 , ang equation ah 2+bx + c = 0 may dalawang magkaibang ugat.

b) Lutasin natin ang equation: 4x 2 - 4x + 1 = 0,

a = 4,b= - 4, c = 1,D = b 2 - 4 ac = (-4) 2 - 4 4 1= 16 - 16 = 0,

D = 0, isang ugat;

Kaya, kung ang discriminant ay zero, i.e. b 2 - 4 ac = 0 , pagkatapos ay ang equation

ah 2+bx + c = 0 may iisang ugat

sa) Lutasin natin ang equation: 2x 2 + 3x + 4 = 0,

a = 2,b= 3, c = 4,D = b 2 - 4 ac = 3 2 - 4 2 4 = 9 - 32 = - 13 , D < 0.

Ang equation na ito ay walang mga ugat.

Kaya, kung ang discriminant ay negatibo, i.e. b 2 - 4 ac < 0 ,

ang equation ah 2+bx + c = 0 walang ugat.

Formula (1) ng mga ugat ng quadratic equation ah 2+bx + c = 0 nagbibigay-daan sa iyo upang mahanap ang mga ugat anuman quadratic equation (kung mayroon man), kabilang ang binawasan at hindi kumpleto. Ang pormula (1) ay ipinahayag sa salita tulad ng sumusunod: ang mga ugat ng isang quadratic equation ay katumbas ng isang fraction na ang numerator ay katumbas ng pangalawang coefficient, na kinuha gamit ang kabaligtaran na sign, kasama ang minus ang square root ng square ng coefficient na ito nang walang apat na beses ang produkto ng unang koepisyent ng libreng term, at ang denominator ay dalawang beses sa unang koepisyent.

4. PARAAN: Solusyon ng mga equation gamit ang Vieta's theorem.

Tulad ng nalalaman, ang ibinigay na quadratic equation ay may anyo

x 2+px + c = 0. (1)

Ang mga ugat nito ay nagbibigay-kasiyahan sa Vieta theorem, na kung kailan a =1 may porma

x 1 x 2 = q,

x 1 + x 2 = - p

Mula dito maaari nating iguhit ang mga sumusunod na konklusyon (ang mga palatandaan ng mga ugat ay maaaring mahulaan mula sa mga coefficient p at q).

a) Kung ang termino ng buod q ng pinababang equation (1) ay positibo ( q > 0 ), pagkatapos ang equation ay may dalawang ugat ng parehong tanda at ito ang inggit ng pangalawang koepisyent p. Kung ang R< 0 , kung gayon ang parehong mga ugat ay negatibo kung R< 0 , pagkatapos ang parehong mga ugat ay positibo.

Halimbawa,

x 2 – 3 x + 2 = 0; x 1 = 2 at x 2 = 1, bilang q = 2 > 0 at p = - 3 < 0;

x 2 + 8 x + 7 = 0; x 1 = - 7 at x 2 = - 1, bilang q = 7 > 0 at p= 8 > 0.

b) Kung isang libreng miyembro q ng pinababang equation (1) ay negatibo ( q < 0 ), pagkatapos ang equation ay may dalawang ugat ng magkaibang tanda, at ang mas malaking ugat sa absolute value ay magiging positibo kung p < 0 , o negatibo kung p > 0 .

Halimbawa,

x 2 + 4 x – 5 = 0; x 1 = - 5 at x 2 = 1, bilang q= - 5 < 0 at p = 4 > 0;

x 2 – 8 x – 9 = 0; x 1 = 9 at x 2 = - 1, bilang q = - 9 < 0 at p = - 8 < 0.

5. PARAAN: Paglutas ng mga equation gamit ang "transfer" method.

Isaalang-alang ang quadratic equation

ah 2+bx + c = 0, saan isang ≠ 0.

Ang pagpaparami ng parehong bahagi nito sa pamamagitan ng a, makuha natin ang equation

isang 2 x 2 + abx + ac = 0.

Hayaan ah = y, saan x = y/a; pagkatapos ay dumating tayo sa equation

y 2+sa pamamagitan ng+ ac = 0,

katumbas ng isang ito. mga ugat nito 1 at sa 2 ay matatagpuan gamit ang Vieta's theorem.

Sa wakas nakuha namin

x 1 \u003d y 1 / a at x 1 \u003d y 2 / a.

Sa pamamaraang ito, ang koepisyent a ay pinarami ng libreng termino, na parang "itinapon" dito, samakatuwid ito ay tinatawag paraan ng paglipat. Ginagamit ang pamamaraang ito kapag madaling mahanap ang mga ugat ng isang equation gamit ang teorem ng Vieta at, higit sa lahat, kapag ang discriminant ay isang eksaktong parisukat.

Halimbawa.

Solusyonan natin ang equation 2x 2 - 11x + 15 = 0.

Desisyon."Ilipat" natin ang koepisyent 2 sa libreng termino, bilang isang resulta makuha natin ang equation

y 2 - 11y + 30 = 0.

Ayon sa teorama ni Vieta

y 1 = 5 x 1 = 5/2x 1 = 2,5

y 2 = 6x 2 = 6/2 x 2 = 3.

Sagot: 2.5; 3.

6. PARAAN: Mga katangian ng mga coefficient ng isang quadratic equation.

PERO. Hayaan ang quadratic equation

ah 2+bx + c = 0, saan isang ≠ 0.

1) Kung, a+b+ c \u003d 0 (i.e. ang kabuuan ng mga coefficient ay zero), pagkatapos x 1 \u003d 1,

x 2 \u003d s / a.

Patunay. Hinahati namin ang magkabilang panig ng equation sa pamamagitan ng ≠ 0, nakukuha namin ang pinababang quadratic equation

x 2 + b/ a x + c/ a = 0.

Ayon sa teorama ni Vieta

x 1 + x 2 = - b/ a,

x 1 x 2 = 1 c/ a.

Sa pamamagitan ng kondisyon a-b+ c = 0, saan b= a + c. kaya,

x 1 + x 2 = -a+ b / a \u003d -1 - c / a,

x 1 x 2 \u003d - 1 (- c / a),

mga. x 1 = -1 at x 2 =c/ a, na kailangan naming patunayan.

Mga halimbawa.

1) Lutasin ang equation 345x 2 - 137x - 208 = 0.

Desisyon. Bilang isang +b+ c \u003d 0 (345 - 137 - 208 \u003d 0), pagkatapos

x 1 = 1, x 2 =c/ a = -208/345.

Sagot: 1; -208/345.

2) Lutasin ang equation 132x 2 - 247x + 115 = 0.

Desisyon. Bilang isang +b+ c \u003d 0 (132 - 247 + 115 \u003d 0), pagkatapos

x 1 = 1, x 2 =c/ a = 115/132.

Sagot: 1; 115/132.

B. Kung ang pangalawang koepisyent b = 2 k ay isang even na numero, pagkatapos ay ang formula ng mga ugat

Halimbawa.

Solusyonan natin ang equation 3x2 - 14x + 16 = 0.

Desisyon. Meron kami: a = 3,b= - 14, c = 16,k = - 7 ;

D = k 2 – ac = (- 7) 2 – 3 16 = 49 – 48 = 1, D > 0, dalawang magkaibang ugat;