Bir fonksiyonun sürekli olduğu nasıl anlaşılır? Bir fonksiyonun bir noktada sürekliliği. sürekli fonksiyon değişimi nedir

Bir fonksiyonun bir noktada sürekliliğinin tanımı verilmiştir. Heine'ye göre, Cauchy'ye göre ve artımlar cinsinden eşdeğer tanımlar dikkate alınır. Bir segmentin uçlarında tek taraflı sürekliliğin tanımı. Devamsızlık beyanı. Heine ve Cauchy tanımlarını kullanarak bir fonksiyonun sürekliliğini kanıtlamanın gerekli olduğu örnekler analiz edilmiştir.

İçerik

Ayrıca bakınız: Bir fonksiyonun limiti - tanımlar, teoremler ve özellikler

Bir noktada süreklilik

Bir fonksiyonun bir noktada sürekliliğini belirleme
f fonksiyonu (x) isminde x'te sürekli 0 Mahalle U (x0) bu nokta ve eğer x limiti x'e eğilimliyse 0 vardır ve x'deki fonksiyonun değerine eşittir 0 :
.

Burada x olduğu varsayılır 0 bitiş noktasıdır. İçindeki bir fonksiyonun değeri yalnızca sonlu bir sayı olabilir.

Süreklilik tanımı sağ (sol)
f fonksiyonu (x) isminde x noktasında sağda (solda) sürekli 0 , eğer bu noktanın sağ (sol) bir komşuluğunda tanımlanmışsa ve x noktasında sağ (sol) limit ise 0 fonksiyonun x noktasındaki değerine eşittir 0 :
.

Örnekler

örnek 1

Heine ve Cauchy tanımlarını kullanarak fonksiyonun tüm x için sürekli olduğunu kanıtlayın.

Rastgele bir sayı olsun. bunu kanıtlayalım verilen fonksiyon noktasında süreklidir. Fonksiyon tüm x için tanımlanmıştır. Bu nedenle, bir noktada ve herhangi bir komşuluğunda tanımlanır.

Heine'nin tanımını kullanıyoruz

Kullanırız . Şuna yakınsayan rastgele bir dizi olsun: . Dizilerin çarpımının limit özelliğini uygulayarak şunları elde ederiz:
.
yakınsayan keyfi bir dizi olduğundan, o zaman
.
Sürekliliği kanıtlanmıştır.

Cauchy tanımını kullanıyoruz

Kullanırız .
Olayı ele alalım. Noktanın herhangi bir komşuluğunda bir fonksiyon düşünme hakkımız var. Bu nedenle, olduğunu varsayacağız
(P1.1) .

Formülü uygulayalım:
.
(A1.1) göz önüne alındığında, tahmin edelim:

;
(S1.2) .

(A1.2) uygulayarak, farkın mutlak değerini tahmin ediyoruz:
;
(S1.3) .
.
Eşitsizliklerin özelliklerine göre, if (A1.3) tutar, if ve if , o zaman .

Şimdi bir noktayı düşünün. Bu durumda
.
.

.
Bu, fonksiyonun noktada sürekli olduğu anlamına gelir.

Benzer şekilde, n'nin bir doğal sayı olduğu fonksiyonun tüm gerçek eksende sürekli olduğu kanıtlanabilir.

Örnek 2

fonksiyonunun herkes için sürekli olduğunu ispatlayın.

Verilen fonksiyon 'de tanımlanmıştır. noktasında sürekli olduğunu ispatlayalım.

Olayı ele alalım.
Noktanın herhangi bir komşuluğunda bir fonksiyon düşünme hakkımız var. Bu nedenle, olduğunu varsayacağız
(P2.1) .

Formülü uygulayalım:
(P2.2) .
İzin vermek . Sonra
.

(A2.1)'i dikkate alarak bir tahminde bulunuruz:

.
Böyle,
.

Bu eşitsizliği uygulayarak ve (A2.2) kullanarak farkı tahmin ederiz:

.
Böyle,
(P2.3) .

Pozitif sayıları tanıtıyoruz ve onları ilişkilerle ilişkilendiriyoruz:
.
Eşitsizliklerin özelliklerine göre, if (A2.3) tutar, if ve if , o zaman .

Bu, herhangi bir pozitif için her zaman olduğu anlamına gelir. Sonra eşitsizliği sağlayan tüm x için aşağıdaki eşitsizlik otomatik olarak sağlanır:
.
Bu, fonksiyonun noktada sürekli olduğu anlamına gelir.

Şimdi bir noktayı düşünün. bunu göstermemiz lazım verilen fonksiyon bu noktada sağda süreklidir. Bu durumda
.
Pozitif sayılar giriyoruz ve:
.

Bu, herhangi bir pozitif için her zaman olduğunu gösterir. O halde tüm x için aşağıdaki eşitsizlik geçerlidir:
.
Demek oluyor . Yani fonksiyon noktasında sağ-süreklidir.

Benzer şekilde, n'nin bir doğal sayı olduğu fonksiyonun için sürekli olduğu kanıtlanabilir.

Referanslar:
O.I. iblisler. Matematiksel analiz üzerine dersler. Bölüm 1. Moskova, 2004.
L.D. Kudryavtsev. Matematiksel analiz kursu. Cilt 1. Moskova, 2003.
SANTİMETRE. Nikolski. Matematiksel analiz kursu. Cilt 1. Moskova, 1983.

Ayrıca bakınız:

Bu dersimizde bir fonksiyonun sürekliliğini nasıl kuracağımızı öğreneceğiz. Bunu, ve olarak yazılmış olmalarına rağmen, hiç de korkutucu olmayan, tek taraflı - sağ ve sol sınırlar yardımıyla yapacağız.

Fakat genel olarak bir fonksiyonun sürekliliği nedir? Kesin bir tanıma gelene kadar, kalemi kağıttan kaldırmadan çizilebilecek bir çizgi hayal etmenin en kolay yolu. Böyle bir çizgi çizilirse, süreklidir. Bu doğru, sürekli bir fonksiyonun grafiğidir.

Grafiksel olarak, grafiği o noktada "kırılmazsa" bir fonksiyon bir noktada süreklidir. Böyle bir sürekli fonksiyonun grafiği, aşağıdaki şekilde gösterilmiştir.

Bir fonksiyonun limit üzerinden sürekliliğinin tanımı. Bir fonksiyon bir noktada üç koşulda süreklidir:

1. Fonksiyon noktasında tanımlanır.

Yukarıdaki koşullardan en az biri sağlanmazsa, fonksiyon bir noktada sürekli değildir. Aynı zamanda fonksiyonun kesintiye uğradığını ve grafiğin kesintiye uğradığı grafik üzerindeki noktalara fonksiyonun kırılma noktaları olarak adlandırıldığını söylüyorlar. x=2 noktasında kesintiye uğrayan böyle bir fonksiyonun grafiği aşağıdaki şekilde gösterilmiştir.

örnek 1İşlev f(x) aşağıdaki gibi tanımlanır:

Bu fonksiyon dallarının sınır noktalarının her birinde, yani noktalarında sürekli olacak mı? x = 0 , x = 1 , x = 3 ?

Karar. Her bir sınır noktasında fonksiyonun sürekliliği için her üç koşulu da kontrol ederiz. İlk koşul karşılandı çünkü fonksiyon tanımlı sınır noktalarının her birinde, fonksiyonun tanımından sonra gelir. Kalan iki koşulu kontrol etmek için kalır.

Nokta x= 0 . Bu noktada sol limiti bulun:

Sağdaki limiti bulalım:

x= 0, fonksiyonun bu noktayı içeren dalında, yani ikinci dalda bulunmalıdır. Onları buluyoruz:

Gördüğünüz gibi, fonksiyonun limiti ve fonksiyonun noktadaki değeri x= 0 eşittir. Bu nedenle, fonksiyon noktada süreklidir x = 0 .

Nokta x= 1. Bu noktada sol limiti bulun:

Sağdaki limiti bulalım:

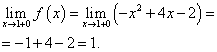
Bir noktada fonksiyon limiti ve fonksiyon değeri x= 1, fonksiyonun bu noktayı içeren dalında, yani ikinci dalda bulunmalıdır. Onları buluyoruz:

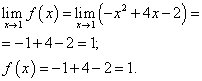Bir noktada fonksiyon limiti ve fonksiyon değeri x= 1 eşittir. Bu nedenle, fonksiyon noktada süreklidir x = 1 .

Nokta x= 3 . Bu noktada sol limiti bulun:

Sağdaki limiti bulalım:

Bir noktada fonksiyon limiti ve fonksiyon değeri x= 3, fonksiyonun bu noktayı içeren dalında, yani ikinci dalda bulunmalıdır. Onları buluyoruz:

Bir noktada fonksiyon limiti ve fonksiyon değeri x= 3 eşittir. Bu nedenle, fonksiyon noktada süreklidir x = 3 .

Ana sonuç: bu fonksiyon her sınır noktasında süreklidir.

Sürekli fonksiyon değişimi nedir?

Bir fonksiyondaki sürekli bir değişiklik, bağımsız değişkendeki küçük bir değişikliğin fonksiyonda küçük bir değişikliğe yol açtığı, atlamalar olmaksızın kademeli bir değişiklik olarak tanımlanabilir.

Bu sürekli fonksiyon değişimini bir örnekle gösterelim.

Bir yükün masanın üzerindeki bir ipe asılmasına izin verin. Bu yükün etkisi altında iplik gerilir, bu nedenle mesafe ben ipliğin askı noktasından itibaren yük, yükün kütlesinin bir fonksiyonudur m, yani ben = f(m) , m≥0 .

Yükün kütlesini biraz değiştirirsek, mesafe ben küçük değişiklik: küçük değişiklik m küçük değişikliklere karşılık gelir ben. Bununla birlikte, yükün kütlesi ipliğin çekme mukavemetine yakınsa, yükün kütlesindeki küçük bir artış ipliğin kopmasına neden olabilir: mesafe ben aniden artacak ve asma noktasından masa yüzeyine olan mesafeye eşit olacaktır. Fonksiyon Grafiği ben = f(m) şekilde gösterilmiştir. Sitede bu grafik sürekli (düz) bir çizgidir ve kesildiği noktadadır. Sonuç, iki daldan oluşan bir grafiktir. fonksiyonu hariç tüm noktalarda ben = f(m) süreklidir ve bir noktada süreksizliği vardır.

Süreklilik için bir fonksiyonun incelenmesi, hem bağımsız bir görev hem de fonksiyonun eksiksiz bir çalışmasının ve grafiğinin oluşturulmasının aşamalarından biri olabilir.

Aralıktaki bir fonksiyonun sürekliliği

fonksiyon olsun y = f(x) aralığında tanımlı ] a, b[ ve bu aralığın her noktasında süreklidir. O zaman aralıkta sürekli denir ] a, b[ . ]- ∞ biçimindeki aralıklarla bir fonksiyonun sürekliliği kavramı benzer şekilde tanımlanır, b[ , ]a, + ∞[ , ]- ∞, + ∞[ . Şimdi fonksiyona izin ver y = f(x) aralıkta tanımlanan [ a, b] . Bir aralık ile bir doğru parçası arasındaki fark, aralığın sınır noktalarının aralığa dahil edilmemesi, ancak doğru parçasının sınır noktalarının parçaya dahil edilmesidir. Burada sözde tek taraflı süreklilikten bahsetmeliyiz: a, aralıkta kalmak [ a, b] , sadece sağdan ve noktaya yaklaşabiliriz b- sadece solda. İşlev, segmentte sürekli olarak adlandırılır [ a, b] , bu segmentin tüm iç noktalarında sürekli ise, noktasında sağda sürekli a ve noktada sürekli sol b.

Aşağıdakilerden herhangi biri sürekli bir fonksiyon örneğidir. temel fonksiyonlar. Her temel fonksiyon, tanımlandığı herhangi bir segmentte süreklidir. Örneğin, ve fonksiyonları herhangi bir aralıkta süreklidir [ a, b] , fonksiyon segmentte süreklidir [ 0 , b] , fonksiyon nokta içermeyen herhangi bir segmentte süreklidir. a = 2 .

Örnek 4 Süreklilik için fonksiyonu araştırın.

Karar. İlk koşulu kontrol edelim. Fonksiyon - 3 ve 3 noktalarında tanımlanmamıştır. Sayı doğrusu üzerinde fonksiyonun sürekliliği için koşullardan en az biri karşılanmamıştır. Bu nedenle, bu fonksiyon aralıklarda süreklidir.

Örnek 5 Parametrenin hangi değerinde olduğunu belirleyin a boyunca sürekli etki alanları işlev

Karar.

Sağdaki limiti bulalım:

noktasındaki değerin belli olduğu açıktır. x= 2 eşit olmalıdır balta :

a = 1,5 .

Örnek 6 Parametrelerin hangi değerlerinde olduğunu belirleyin a ve b boyunca sürekli etki alanları işlev

Karar.
Aşağıdaki noktada fonksiyonun sol sınırını bulunuz:

Bu nedenle, noktadaki değer 1'e eşit olmalıdır:

Şu noktada sol taraftaki fonksiyonu bulalım:

Açıkçası, fonksiyonun noktadaki değeri şuna eşit olmalıdır:

Cevap: fonksiyon tüm tanım alanı boyunca süreklidir. a = 1; b = -3 .

Sürekli fonksiyonların temel özellikleri

Matematik, her şeyden önce çeşitli hareket yasalarını inceleyerek sürekli bir fonksiyon kavramına geldi. Uzay ve zaman sonsuzdur ve bağımlılıklar yollar gibidir s zamandan t, kanunla ifade edilen s = f(t) , sürekli bir örnek verir fonksiyonlar f(t) . Isıtılan suyun sıcaklığı da sürekli değişir, aynı zamanda zamanın sürekli bir fonksiyonudur: T = f(t) .

AT matematiksel analiz sürekli fonksiyonların sahip olduğu bazı özellikler ispatlanmıştır. Bu özelliklerden en önemlilerini sunuyoruz.

1. Bir aralıkta sürekli bir fonksiyon, aralığın sonunda farklı işaretlerin değerlerini alıyorsa, bu segmentin bir noktasında değeri alır. sıfır. Daha resmi olarak, bu özellik, ilk Bolzano-Cauchy teoremi olarak bilinen bir teoremde verilir.

2. İşlev f(x), aralıkta sürekli [ a, b] , uç noktalardaki değerler arasındaki tüm ara değerleri yani aradaki değerleri alır. f(a) ve f(b) . Daha resmi olarak, bu özellik ikinci Bolzano-Cauchy teoremi olarak bilinen bir teoremde verilir.

Tanım. Bir x 0 noktasının çevresinde tanımlanan f(x) fonksiyonuna denir. bir noktada sürekli x 0, eğer fonksiyonun limiti ve bu noktadaki değeri eşitse, yani.

Aynı gerçek farklı şekilde yazılabilir:

Tanım. f(x) fonksiyonu, x 0 noktasının bir komşuluğunda tanımlanmışsa, ancak x 0 noktasında sürekli değilse, o zaman fonksiyon olarak adlandırılır. süreksiz fonksiyonu ve x 0 noktası kırılma noktasıdır.

Sürekli fonksiyon örneği:

0 x 0 - x 0 x 0 + x

P süreksiz fonksiyon örneği:

Tanım. Herhangi bir pozitif sayı >0 için, koşulu sağlayan herhangi bir x için >0 gibi bir sayı varsa, f(x) fonksiyonu x 0 noktasında sürekli olarak adlandırılır.

gerçek eşitsizlik
.

Tanım. f(x) işlevi çağrılır sürekli x \u003d x 0 noktasında, fonksiyonun x 0 noktasındaki artışı sonsuz küçük bir değerse.

f(x) = f(x 0) + (x)

burada (x), xx 0'da sonsuz küçüktür.

Sürekli fonksiyonların özellikleri.

1) x 0 noktasında sürekli fonksiyonların toplamı, farkı ve çarpımı, x 0 noktasında sürekli bir fonksiyondur.

2) İki sürekli fonksiyonun bölümü - g(x)'in x 0 noktasında sıfıra eşit olmaması şartıyla sürekli bir fonksiyondur.

3) Sürekli fonksiyonların süperpozisyonu sürekli bir fonksiyondur.

Bu özellik aşağıdaki gibi yazılabilir:

Eğer u = f(x), v = g(x), x = x 0 noktasında sürekli fonksiyonlarsa, v = g(f(x)) fonksiyonu da bu noktada sürekli bir fonksiyondur.

Yukarıdaki özelliklerin geçerliliği limit teoremleri kullanılarak kolaylıkla kanıtlanabilir.

Bazı temel fonksiyonların sürekliliği.

1) f(x) = C, C = const işlevi, tüm tanım alanında sürekli bir işlevdir.

2) Rasyonel fonksiyon
paydanın sıfıra gittiği değerler hariç, tüm x değerleri için süreklidir. Böylece, bu tür bir fonksiyon, tüm tanım alanı boyunca süreklidir.

3) Trigonometrik fonksiyonlar sin ve cos tanım alanlarında süreklidir.

y = sinx fonksiyonu için özellik 3'ü ispatlayalım.

y = sin(x + x) - sinx fonksiyonunun artışını veya dönüşümden sonra yazalım:

Gerçekten de, iki fonksiyonun çarpımının bir sınırı vardır.
ve
. Bu durumda kosinüs fonksiyonu х0'da sınırlı bir fonksiyondur.
, dan beri

sinüs fonksiyonu limiti
, o zaman х0'da sonsuz küçüktür.

Böylece, sınırlı bir fonksiyonun bir ürünü ve bir sonsuz küçük olanın bir ürünü vardır, dolayısıyla bu ürün, yani. y fonksiyonu sonsuz küçüktür. Yukarıda tartışılan tanımlara göre, y \u003d sinx işlevi, tanım alanından herhangi bir x \u003d x 0 değeri için sürekli bir işlevdir, çünkü bu noktadaki artışı sonsuz küçük bir değerdir.

Süreksizlik noktaları ve sınıflandırılması.

Belki de bu noktanın kendisi dışında, x 0 noktasının bir komşuluğunda sürekli olan bir f(x) fonksiyonunu ele alalım. Bir fonksiyonun kırılma noktasının tanımından, eğer fonksiyon bu noktada tanımlı değilse veya bu noktada sürekli değilse, x = x 0 bir kırılma noktasıdır.

Bir fonksiyonun sürekliliğinin tek taraflı olabileceği de unutulmamalıdır. Bunu aşağıdaki şekilde açıklayalım.

, o zaman fonksiyonun sağ sürekli olduğu söylenir.

Tek taraflı limit ise (yukarıya bakın)
, o zaman fonksiyonun solda sürekli olduğu söylenir.

Tanım. x 0 noktasına denir kırılma noktası f(x) fonksiyonu, f(x) x 0 noktasında tanımlı değilse veya bu noktada sürekli değilse.

Tanım. x 0 noktasına denir 1. tür süreksizlik noktası, eğer bu noktada f(x) fonksiyonunun sonlu fakat eşit olmayan sol ve sağ limitleri varsa.

Bu tanımın şartlarını yerine getirmek için fonksiyonun x \u003d x 0 noktasında tanımlanması gerekli değildir, solunda ve sağında tanımlanması yeterlidir.

Tanımdan, 1. türün süreksizlik noktasında, fonksiyonun yalnızca sonlu bir sıçramaya sahip olabileceği sonucuna varabiliriz. Bazı özel durumlarda, 1. türün süreksizlik noktası bazen de denir. tek kullanımlık kırılma noktası, ancak daha fazlası aşağıda.

Tanım. x 0 noktasına denir 2. türün kırılma noktası, eğer bu noktada f(x) fonksiyonu tek taraflı limitlerden en az birine sahip değilse veya en az biri sonsuz ise.

Bir fonksiyonun bir aralıkta ve bir segmentte sürekliliği.

Tanım. f(x) işlevi çağrılır aralıkta sürekli (segment), aralığın herhangi bir noktasında (segment) sürekli ise.

Bu, segment veya aralığın uçlarında fonksiyonun sürekliliğini gerektirmez, segment veya aralığın uçlarında sadece tek taraflı süreklilik gereklidir.

Bir aralıkta sürekli fonksiyonların özellikleri.

Özellik 1: (Weierstrass'ın ilk teoremi (Weierstrass Karl (1815-1897) - Alman matematikçi)). Bir aralıkta sürekli olan bir fonksiyon bu aralıkta sınırlandırılır, yani. segmentte –M  f(x)  M koşulu sağlanır.

Bu özelliğin kanıtı, x 0 noktasında sürekli olan bir fonksiyonun bazı komşuluklarında sınırlı olduğu gerçeğine dayanır ve eğer parçayı x 0 noktasına “büzüşen” sonsuz sayıda parçaya bölerseniz. , daha sonra x 0 noktasının bir komşuluğu oluşur.

Özellik 2: Aralıkta sürekli olan bir fonksiyon maksimum ve minimum değerlerini alır.

Onlar. x 1 ve x 2'nin öyle değerleri vardır ki f (x 1) = m, f (x 2) = M ve

m  f(x)  M

Fonksiyonun bir segmentte ve birkaç kez alabileceği bu maksimum ve minimum değerleri not ediyoruz (örneğin, f (x) = sinx).

Bir fonksiyonun bir segmentteki en büyük ve en küçük değeri arasındaki farka denir. tereddüt segmentte işlev görür.

Özellik 3: (İkinci Bolzano-Cauchy teoremi). Bir segment üzerinde sürekli olan bir fonksiyon, bu segmentte iki keyfi değer arasındaki tüm değerleri alır.

Mülk 4: f(x) fonksiyonu x = x 0 noktasında sürekli ise, x 0 noktasında fonksiyonun işaretini koruduğu bir komşuluk vardır.

Mülk 5: (Bolzano'nun ilk teoremi (1781-1848) - Cauchy). f(x) fonksiyonu bir doğru parçası üzerinde sürekli ise ve parçanın uçlarında zıt işaretli değerlere sahipse, bu doğru parçasının içinde f(x) = 0 olan bir nokta vardır.

Onlar. eğer işaret(f(a))  işaret(f(b)) ise, o zaman  x 0: f(x 0) = 0.

Misal.

x = -1 noktasında fonksiyon süreklidir x = 1 noktasında 1. tür süreksizlik noktası

Misal. Süreklilik fonksiyonunu araştırın ve varsa süreksizlik noktalarının türünü belirleyin.

x = 0 noktasında fonksiyon süreklidir x = 1 noktasında 1. tür süreksizlik noktası

Heine'nin süreklilik tanımı

Gerçek bir değişkenin \(f\left(x \right)\) fonksiyonunun şu şekilde olduğu söylenir: sürekli \(a \in \mathbb(R)\) (\(\mathbb(R)-\)set noktasında gerçek sayılar) herhangi bir \(\left\( ((x_n)) \right\)\) dizisi için \[\lim\limits_(n \to \infty ) (x_n) = a,\] ilişkisi \[\ lim\limits_(n \to \infty ) f\left(((x_n)) \right) = f\left(a \right).\] Pratikte, aşağıdaki \(3\) sürekliliğini kullanmak uygundur \(x = a\) noktasındaki \(f\left(x \right)\) işlevi için koşullar (aynı anda çalışması gerekir):

\(f\sol(x \sağ)\) işlevi \(x = a\) noktasında tanımlanır;
\(\lim\limits_(x \to a) f\left(x \right)\) sınırı var;
\(\lim\limits_(x \to a) f\left(x \right) = f\left(a \right)\) eşitliği sağlanır.

Cauchy sürekliliğinin tanımı (notasyon \(\varepsilon - \delta\))

Gerçek sayılar kümesini \(\mathbb(R)\) gerçek sayıların başka bir \(B\) alt kümesine eşleyen \(f\left(x \right)\) işlevini düşünün. \(f\left(x \sağ)\) fonksiyonunun olduğu söylenir sürekli \(a \in \mathbb(R)\) noktasında herhangi bir \(\varepsilon > 0\) sayısı için bir \(\delta > 0\) varsa, öyle ki tüm \(x \in \mathbb için) (R)\) ilişkisini sağlayan \[\left| (x - a) \sağ| Argüman ve fonksiyon artışları açısından sürekliliğin tanımı

Sürekliliğin tanımı, argüman ve fonksiyon artışları kullanılarak da formüle edilebilir. Eğer \[\lim\limits_(\Delta x \to 0) \Delta y = \lim\limits_(\Delta x \to 0) \left[ ( f) ise fonksiyon \(x = a\) noktasında süreklidir \left((a + \Delta x) \sağ) - f\left(a \sağ)) \sağ] = 0,\] burada \(\Delta x = x - a\).

Bir fonksiyonun sürekliliğinin yukarıdaki tanımları, gerçek sayılar kümesinde eşdeğerdir.

işlev Bu aralıkta sürekli eğer bu aralığın her noktasında sürekli ise.

süreklilik teoremleri

Teorem 1.
\(f\left(x \right)\) fonksiyonu \(x = a\) noktasında sürekli olsun ve \(C\) bir sabit olsun. O zaman \(Cf\left(x \sağ)\) işlevi de \(x = a\) için süreklidir.

Teorem 2.
\((f\left(x \right))\) ve \((g\left(x \right))\) \(x = a\) noktasında sürekli olan iki fonksiyon verildi. O zaman bu fonksiyonların toplamı \((f\sol(x \sağ)) + (g\left(x \sağ))\) da \(x = a\) noktasında süreklidir.

Teorem 3.
\((f\left(x \right))\) ve \((g\left(x \right))\) işlevlerinin \(x = a\) noktasında sürekli olduğunu varsayalım. O halde bu fonksiyonların \((f\sol(x \sağ)) (g\sol(x \sağ))\) çarpımı da \(x = a\) noktasında süreklidir.

Teorem 4.
\(x = a\) için sürekli olan iki \((f\left(x \right))\) ve \((g\left(x \right))\) işlevi verildi. O zaman bu fonksiyonların \(\large\frac((f\left(x \right)))((g\left(x \right)))\normalsize\) oranı da \(x = a\ için süreklidir ) \((g\left(a \sağ)) \ne 0\).

Teorem 5.
\((f\sol(x \sağ))\) fonksiyonunun \(x = a\) noktasında türevlenebilir olduğunu varsayalım. O halde \((f\left(x \right))\) fonksiyonu bu noktada süreklidir (yani türevlenebilirlikten fonksiyonun o noktada sürekli olduğu sonucu çıkar; tersi doğru değildir).

Teorem 6 (Limit değer teoremi).
Eğer bir fonksiyon \((f\left(x \right))\) kapalı ve sınırlı bir \(\left[ (a,b) \sağ]\ aralığında sürekliyse), o zaman verilen aralık. Başka bir deyişle, \(m\) ve \(M\) sayıları vardır, öyle ki \(\left[ (a,b) \sağ]\) aralığındaki tüm \(x\) için \ (Şekil 1) .


Şekil 1		İncir. 2

Teorem 7 (Ara değer teoremi).
\((f\left(x \right))\) işlevi kapalı ve sınırlı bir aralık \(\left[ (a,b) \sağ]\) üzerinde sürekli olsun. O halde, eğer \(c\), \((f\left(a \right))\)'den büyük ve \((f\left(b \right))\'den küçük bir sayıysa), o zaman bir sayı vardır \(( x_0)\), öyle ki \ Bu teorem Şekil 2'de gösterilmiştir.

Temel fonksiyonların sürekliliği

Herşey temel fonksiyonlar tanım alanlarının herhangi bir noktasında süreklidir.

fonksiyon denir temel , sınırlı sayıda kompozisyon ve kombinasyondan yapılmışsa
(\(4\) işlemlerini kullanarak - toplama, çıkarma, çarpma ve bölme) . Bir demet temel temel işlevler içerir:

Eğitim Kurumu "Belarus Devleti

Tarım Akademisi"

Yüksek Matematik Bölümü

yönergeler

"Tek değişkenli fonksiyonların sürekliliği" konusunun incelenmesi üzerine

Muhasebe Fakültesi öğrencilerinin yazışma formunun alınması

eğitim (NISPO)

Gorki, 2013

Tek değişkenli fonksiyonların sürekliliği

Tek taraflı limitler

fonksiyon olsun
sette tanımlanmış
. Bir fonksiyonun tek taraflı limitleri kavramını tanıtalım.
. Bu tür değerleri dikkate alacağız. X, ne
. Demek oluyor
, her zaman solunda kalan
de
o zaman denir sol sınır noktada bu fonksiyon (ya da ne zaman
) ve belirtilen

şimdi izin ver
, her zaman sağda kalan , yani daha uzun kalmak . Fonksiyonun bir limiti varsa
, o zaman denir sağ sınır noktada bu fonksiyon ve belirtilen

Sol ve sağ limitler denir tek taraflı limitler bir noktada işlev görür.

Bir fonksiyonun bir noktada tek taraflı limitleri varsa ve bunlar birbirine eşitse, fonksiyonun bu noktada limiti aynıdır.:

Bir fonksiyonun bir noktada tek taraflı limitleri ise var, ancak birbirine eşit değil, o zaman bu noktada fonksiyonun limiti mevcut değil .

Bir noktada bir fonksiyonun sürekliliği

fonksiyon olsun
bazı sette tanımlanmış D. Bağımsız değişken olsun X(başlangıç) değerlerinden birinden hareket eder
başka bir (son) değere . Son ve ilk değerler arasındaki farka denir. artış miktarları X ve belirtilen
. Artış pozitif veya negatif olabilir. İlk durumda, değer X hareket ederken ile X artar ve ikinci durumda - azalır.

bağımsız değişken ise X biraz destek alır
, ardından fonksiyon
bir artış alır
. Gibi
, o zamanlar .

fonksiyon artışı
noktada fark denir, burada
bağımsız değişkenin artışıdır.

Bir fonksiyonun bir noktadaki sürekliliği için birkaç tanım vermek mümkündür.

fonksiyon denir aralıkta sürekli eğer bu aralığın her noktasında sürekli ise. Bir fonksiyonun geometrik sürekliliği
kapalı bir aralıkta, fonksiyonun grafiğinin kesintisiz düz bir çizgi olduğu anlamına gelir.

Bir aralıkta sürekli fonksiyonlar, aşağıdaki ifadelerle ifade edilen önemli özelliklere sahiptir.

eğer fonksiyon
segmentte sürekli [ a, b], o zaman bu segmentte sınırlanır.

eğer fonksiyon
segmentte sürekli [ a, b], daha sonra bu segmentte minimum ve maksimum değerlerine ulaşır.

eğer fonksiyon
segmentte sürekli [ a, b] ve
, o zaman sayı ne olursa olsun İle sayılar arasında ANCAK ve AT, bir nokta var
, ne
.

Bu açıklamadan şu sonucu çıkar ki, eğer fonksiyon
sürekli [ a, b] ve bu segmentin uçlarında farklı işaretlerin değerlerini alır, o zaman bu segment üzerinde en az bir nokta vardır. c fonksiyonun kaybolduğu yer.

Aşağıdaki ifade doğrudur: sürekli fonksiyonlar üzerinde aritmetik işlemler yapılırsa, sonuç sürekli bir fonksiyondur.İ.

örnek 1 .

noktada
.

Karar . işlev değeri
orada
. noktasında fonksiyonun tek taraflı limitlerini hesaplayalım.
:

Tek taraflı limitler olduğu için
birbirine ve bu noktada fonksiyonun değerine eşitse, bu noktada bu fonksiyon süreklidir.
.

3. Temel fonksiyonların sürekliliği

işlevi düşünün
. Bu sabit fonksiyon herhangi bir noktada süreklidir. , gibi
.

İşlev
ayrıca her noktada süreklidir
, gibi
. Gibi
, daha sonra yukarıdaki ifadeye dayanarak Aritmetik işlemler sürekli fonksiyonlar üzerinde
sürekli olacaktır. Fonksiyonlar da sürekli olacaktır.
.

Benzer şekilde, kalan temel fonksiyonların sürekliliğini gösterebiliriz.

Böylece, herhangi bir temel işlev, tanım alanında süreklidir, yani. temel bir işlevin tanım alanı, süreklilik alanıyla çakışır.

Karmaşık ve ters fonksiyonların sürekliliği

fonksiyon olsun
noktada sürekli , ve işlev
noktada sürekli
. Daha sonra karmaşık fonksiyon
noktada sürekli . Bu, eğer karmaşık bir fonksiyon sürekli fonksiyonlardan oluşuyorsa, o zaman da sürekli olacağı anlamına gelir, yani. sürekli bir fonksiyondan sürekli bir fonksiyon sürekli bir fonksiyondur . Bu tanım, sonlu sayıda sürekli fonksiyona kadar uzanır.

Bu tanımdan, sürekli bir fonksiyonun işareti altında limite geçilebileceği sonucu çıkar:

Bu, fonksiyon sürekli ise, limitin işareti ile fonksiyonun işaretinin yer değiştirebileceği anlamına gelir.

fonksiyon olsun
a, b]. Daha sonra ters fonksiyonu
tanımlı, kesinlikle monoton ve aralıkta süreklidir [ A, B], nerede
.

Kesme noktaları ve sınıflandırılmasıİ

Zaten bildiğimiz gibi, eğer fonksiyon
sette tanımlanmış D ve noktada
kondisyon
, o zaman fonksiyon o noktada süreklidir. Bu süreklilik koşulu sağlanmazsa, o zaman noktada X 0 işlevinde bir boşluk var.

Nokta isminde birinci türden kırılma noktası fonksiyonlar
, bu noktada fonksiyonun birbirine eşit olmayan sonlu tek taraflı limitleri varsa, yani. . Aynı zamanda, değer

isminde aniden fonksiyonlar
noktada .

Nokta isminde kırılma noktası fonksiyonlar
, fonksiyonun bu noktadaki tek taraflı limitleri birbirine eşitse ve fonksiyonun bu noktadaki değerine eşit değilse, yani. Bu durumda, noktadaki süreksizliği ortadan kaldırmak için koymak gerek

Nokta X 0 denir ikinci türün kırılma noktası fonksiyonlar
tek taraflı limitlerden en az biri ise
veya
bu noktada ya yoktur ya da sonsuza eşittir.

Örnek 2 . Bir fonksiyonun sürekliliği için araştırma yapın

Karar . Fonksiyon tanımlı ve nokta hariç tüm gerçek doğru üzerinde süreklidir.
. Bu noktada, fonksiyon bir süreksizliğe sahiptir. noktasında fonksiyonun tek taraflı limitlerini bulalım.
:

noktadan beri
tek taraflı limitler birbirine eşittir ve bu noktadaki fonksiyon tanımlanmaz, o zaman nokta
bir kırılma noktasıdır. Bu noktadaki boşluğu ortadan kaldırmak için, işlevi ayarlayarak yeniden tanımlamak gerekir.
.

Örnek 3 . Bir fonksiyonun sürekliliği için araştırma yapın

Karar . Fonksiyon, aşağıdakiler hariç tüm gerçek sayılar kümesinde tanımlı ve süreklidir.
. Bu noktada, fonksiyon bir süreksizliğe sahiptir. fonksiyonunun tek taraflı limitlerini bulalım.
:

Bu fonksiyon noktada olduğu için
birbirine eşit olmayan sonlu tek taraflı limitlere sahipse, bu nokta birinci türden bir süreksizlik noktasıdır. Bir noktada fonksiyon atlama
eşittir .

Bilginin kendi kendini kontrol etmesi için sorular

Argüman artışı ve fonksiyon artışı ne denir?

Bir fonksiyonun sol (sol) limitine ne denir?

Bir fonksiyonun sağ (sağ) limitine ne denir?

Bir aralıkta bir noktada sürekli olarak adlandırılan fonksiyon nedir?

Bir fonksiyonun kırılma noktası nedir?

Hangi noktaya birinci tür süreksizlik noktası denir?

Hangi noktaya ikinci türden süreksizlik noktası denir?

Hangi noktaya kırılma noktası denir?

Bağımsız çalışma için görevler

Süreklilik için işlevleri inceleyin:

noktada
.