Research work "10 ways to solve quadratic equations". Ways to solve quadratic equations 10 ways to solve square

Department of Education and Science

Kemerovo region

GOU SPO "Mariinsky Agricultural College"

10 WAYS TO SOLUTION

SQUARE EQUATIONS

ax ²+in+c=0

Work completed:

King Faith,

group student 161

specialty 260807 "Technology of catering products"

Supervisor:

Matveeva Olga Vasilievna,

mathematics teacher

Mariinsk, 2013

I Introduction

II. History of occurrence quadratic equations

2. Quadratic equations in ancient Babylon.

3. Quadratic equations in EuropeXIII – XVII centuries

III. Ways to solve quadratic equations

3. Particular cases of solving quadratic equations:

a) coefficient a - very small,

b) coefficient with - very small.

4. Solution of equations using the Vieta theorem.

6. Solution of equations by the method of "transfer".

9. Solving quadratic equations using a nomogram.

IV. Conclusion

V. Literature

I. INTRODUCTION

« It is often more useful for a student of algebra to solve the same problem in three different ways than to solve three or four different problems. By solving one problem with different methods, it is possible to find out by comparison which one is shorter and more efficient. That's how experience is made."

W. Sawyer

Quadratic equations are the foundation on which the majestic edifice of algebra rests. Quadratic equations are widely used in solving varioustrigonometric, exponential, logarithmic, irrational, transcendental equations and inequalities, a large number different types tasks.

The theory of equations occupies a leading place in algebra and mathematics in general. The strength of the theory of equations is that it not only has theoretical significance for the knowledge of natural laws, but also serves practical purposes. Most of life's problems come down to solving various kinds equations, and more often these are equations of a quadratic form.

The quadratic equation is a large and important class of equations that can be solved using both formulas and elementary functions.

AT school course mathematics, we get acquainted with several types of quadratic equations, and work out the solution using standard formulas. At the same time, modern scientific and methodological research shows that the use of a variety of methods and methods can significantly improve the efficiency and quality of studying solutions to quadratic equations.

Thus, there is a need to study various ways of solving quadratic equations.

All of the above definesrelevance research topics.

Problem research is to consider various, including non-standard ways of solving quadratic equations.

Target work is to study theoretical foundations and their application in solving quadratic equations.

Thing research: quadratic equations and their solutions.

Tasks:

Conduct an analysis of the literature on this topic.

To study the history of the development of quadratic equations.

To study various ways of solving quadratic equations, including non-standard ones, and to test the material in practice.

II. HISTORY OF THE ORIGIN OF QUADRATIC EQUATIONS

1. Quadratic equations in India.

Problems for quadratic equations are found in the astronomical tractor "Aryabhattiam", compiled in 499 by the Indian mathematician and astronomer Aryabhata. Another Indian scholar - Brahmagupta (VIIc.) outlined general rule solutions of quadratic equations. The rule of Brahmagupta essentially coincides with the modern one.

In ancient India, public competitions in solving difficult problems were common. In one of the old Indian books, the following is said about such competitions: “As the sun outshines the stars with its brilliance, so scientist man eclipse the glory of another in public meetings, proposing and solving algebraic problems. Tasks were often dressed in poetic form.

Here is one of the problems of the famous Indian mathematicianXII in Bhaskara.

Frisky flock of monkeys

Having eaten power, had fun.

Them squared part eight

Having fun in the meadow

And twelve by vines

They began to jump, hanging ..

How many monkeys were

You tell me, in this flock?

Bhaskara's solution indicates that he knew about the two-valuedness of the roots of quadratic equations.

x 2 - 64 = - 768,

x 2 - 64x +32 2 \u003d - 768 + 1024,

(x - 32) 2 \u003d 256,

x 1 = 16, x 2 = 48

2. Quadratic Equations in Ancient Babylon.

The Babylonians knew how to solve quadratic equations around 2000 BC. Applying modern algebraic notation, we can say that in their cuneiform texts there are, in addition to incomplete ones, such, for example, complete equations.

The rule for solving these equations, stated in the Babylonian texts, coincides essentially with the modern one, but it is not known how the Babylonians came to this rule. Almost all cuneiform texts found so far give only problems with solutions stated in the form of recipes, without instructions as to how

they were found. In spite of high level development of algebra in Babylon, in cuneiform texts there is no concept of a negative number and general methods for solving quadratic equations.

3. Quadratic equations in Europe in XII – XVII centuries

Forms for solving quadratic equations on the model of al-Khwarizmi in Europe were first described in the "Book of Abah", written in 1202 by the Italian mathematician Leonardo Fibonacci. The author independently developed some new algebraic examples problem solving and was the first in Europe to approach the introduction of negative numbers. His book contributed to the spread of algebraic knowledge not only in Italy, but also in Germany, France and other European countries. Many tasks from the "Book of Abah" were transferred to almost all European textbooksXVI – XVII centuries and partially XVIII in.

General rule for solving quadratic equations reduced to a single canonical formX 2 + bx = with with all possible combinations of signs and coefficientsb , c , was formulated in Europe in 1544 by M. Stiefel. Derivation of the formula for solving a quadratic equation in general view Viet has, but Viet recognized only the positive roots of Viet, the famous French scientist, also a lawyer by profession. Italian scientists Tartaglia, Cardano, Bombelli among the first inXVIin. Take into account, in addition to positive, and negative roots. Only inXVIIin. Thanks to the works of Girrard, Descartes, Newton and other scientists, the method of solving quadratic equations takes on a modern look.

III. DIFFERENT WAYS OF SOLVING QUADRATIC EQUATIONS

1. General view of the quadratic equation and standard formulas for its solution.

Equation of the form ax 2 + in + c = 0 (1) , where a, b, c - some numbers, anda ≠ 0, called square.

A quadratic equation is also called an equation of the second degree.

In equation (1) a called first coefficient, in- second coefficient, with - the third coefficient or free member.

Expression of the form D = in 2 – 4ac is called the discriminant (distinguisher) of the quadratic equation.

Recall that the root (or solution) of an equation with an unknownX the number is called, when substituting into the equation instead ofX a correct numerical equation is obtained.

To solve an equation means to find all its roots or show that there are none.

The presence of the roots of the quadratic equation (1) depends on the sign of the discriminantD, so the solution of the equation should begin with the calculationDto find out if the quadratic equation (1) has roots, and if so, how many.

Three cases are possible:

If a D>0, then the quadratic equation (1) has two different real roots:

in 2 - 4ac.

If a D<0, то квадратное уравнение не имеет действительных корней.

Suppose that in some equation we made the following transformation: we opened the brackets, if any, destroyed the denominators, if the equation has fractional terms, moved all the terms to the left side of the equation and made a reduction of similar terms. If after that there is a term containing the unknown squared on the left side of the equation, and there are no terms containing the unknown to a higher degree, then a quadratic equation is obtained. The general form of such an equation is 2 + bx + c = 0.

Note that the coefficienta we can always make positive, changing, if necessary, before all the terms of the equation the signs to the opposite.

Example 1

Find oddsa, in and with for the equation:
.

Decision:

Expanding the brackets:
,

Destroying the denominator: 72 + 2x 2 = 15x 2 + 15x,

We transfer all members to the left side and do the cast: - 13x 2 - 15x + 72 = 0,

Change signs: 13x 2 + 15x - 72 = 0,

Odds a, b , and with the general form of the quadratic equation took in this example the following particular values:a = 13, b = 15 and c = - 72 .

Example 2

Solve the equation:

Solution: >0, two roots;

Answer:

Example 3

Solve the equation:

Decision: D =0, one root;

Answer:

Example 4

Solve the equation:

Decision:<0.

The equation has no real roots.

Answer: There are no real roots.

Considering the solution of quadratic equations, we see that these equations sometimes have two roots, sometimes one, sometimes none. However, they agreed to attribute to quadratic equations in all casestwo roots , it goes without saying that the roots can sometimes be equal, sometimes imaginary. The reason for such an agreement is that the formulas expressing the imaginary roots of an equation have the same properties that belong to real roots, it consists only in performing operations on imaginary quantities, be guided by the rules derived for real quantities, while accepting that (
) 2 = - a. Similarly, when an equation has one root, we can, by considering this root astwo identical, attribute to them the same properties that belong to different roots of the equation. The simplest of these properties is expressed in the following theorem.

Theorem: The sum of the roots of a quadratic equation, in which the coefficient for the unknown in the 2nd degree is 1, is equal to the coefficient for the unknown in the first degree, taken with the opposite sign; the product of the roots of this equation is equal to the free term.

Proof: Denoting by α and β the roots of the equationX 2 +px+ q = 0 , we will have (whatever these roots are)

This product can be found in an abbreviated way, based on the equality (a + b)(a – b) = a 2 – b 2 :

If α and β are roots of the equationOh 2 + bx + c = 0 , or what is the same equation

, then it will have

.

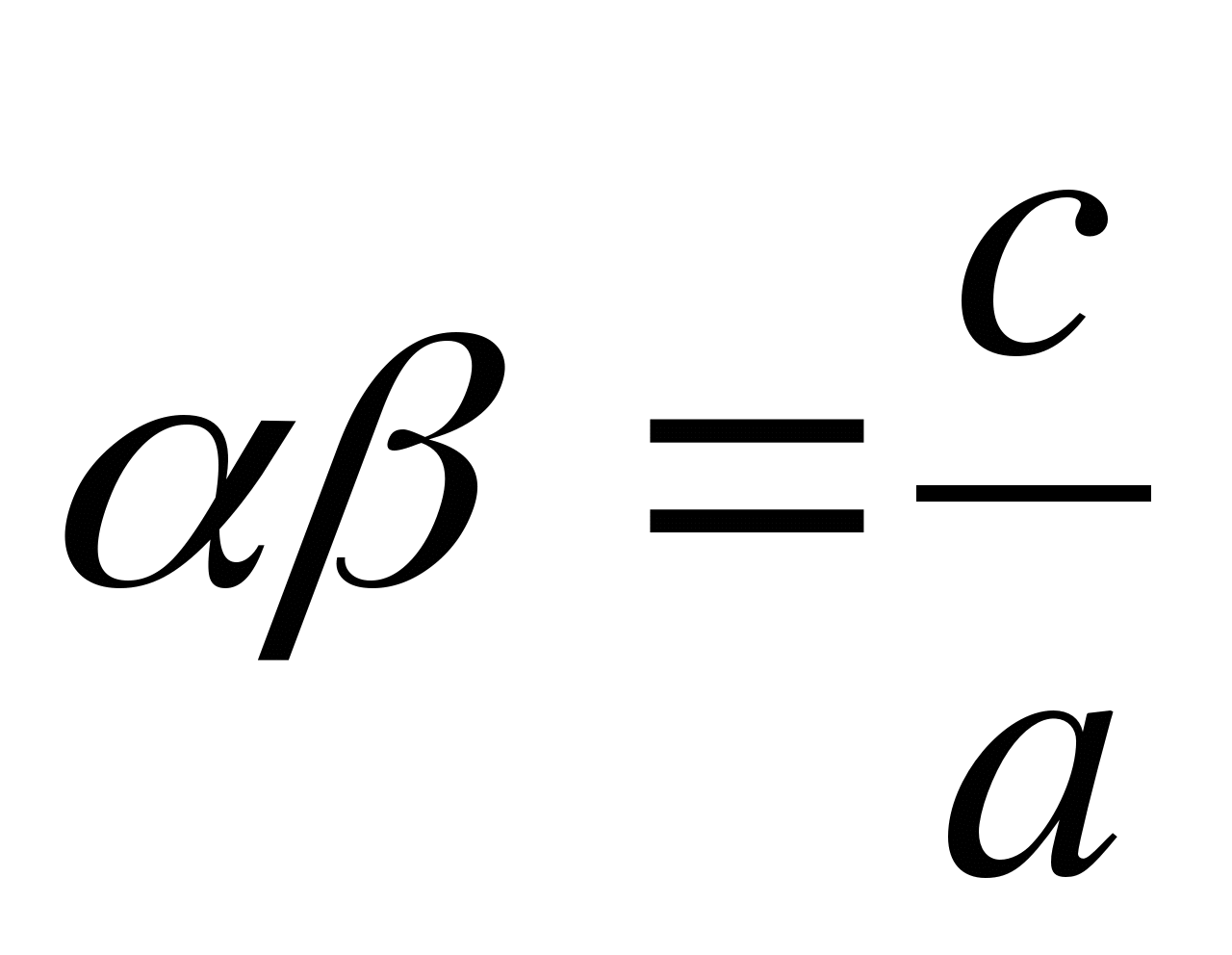Inverse theorem: If quantities α, β, p and q are such that α + β = - R and αβ = q , then β and α are the roots of the equationX 2 +px+ q = 0 .

Proof: It is required to prove that each of the quantitiesβ and α satisfies the equationX 2 +px+ q = 0 . From equality α + β = - p and α \u003d -p - β , after which the equalityαβ = q gives

or
.

Means, β is the root of the equationOh 2 + bx + c = 0 ; in the same way, we can verify thatα is the root of the same equation.

1st consequence. These roots can be used to form a quadratic equation. Let it be required to compose an equation whose roots would be 2 and - 3. Assuming that 2 + (- 3) \u003d - p and 2 (- 3) \u003dq, we find - p \u003d 1, q= - 6. Hence, the desired equation will be

X 2 + x - 6 = 0

Similarly, we find that - 2 and - 2 are the roots of the equation x 2 + 4x + 4 = 0, 3 and 0 are the roots of the equation x 2 - 3x = 0, etc.

2nd corollary. Without solving a quadratic equation, one can determine the signs of its roots if these roots are real. Let, for example, we have the equation x 2 + 8x +10 = 0. Since in this example the number
- qis a positive number, then both roots must be real. Let us determine, without solving the equations, the signs of these roots. To do this, we argue as follows: paying attention first to the free term (+ 10), we see that it has a + sign; so the product of the roots must bepositive , i.e. both roots havethe same signs. To determine which ones, let's pay attention to the coefficient atX (i.e. at +8) it has a + sign; therefore, the sum of the coefficientsnegative ; because the same signs at the roots should beminus .

Similar reasoning can determine the signs at the roots in any other case. So the equation x 2 + 8x - 10 = 0 has roots with different signs

(because their product is negative), and the negative root has a large absolute value (because their sum is negative); equation x 2 - 8 - 10 \u003d 0 also has roots with different signs, but a large absolute value belongs to a positive root.

2. Solution of incomplete quadratic equations.

A quadratic equation is called incomplete when it does not contain a term containingX , or there is no free term. Incomplete quadratic equations can only be of the following three types:

a) ax 2 + c = 0; b) ax 2 + bx= 0; with) ax 2 = 0.

Let's take a look at each solution.

a) From the equation X 2 + c = 0 finds

Oh 2 = - c and x 2 = .

This equality requires that the square of the unknown equals the number ; so the unknown must be equal to the square root of that quantity. This is only possible when the quantity is a positive number, what happens whenwith and a have opposite signs (if, for example,with = - 8, a = + 2, then

Let us denote by the sign only the arithmetic value of the square root and take into account that the square root of a positive number has two values; then, denoting one value throughX 1 , and the other through X 2 , we can write

If numbers with and a have the same sign, then is a negative number; then the equation ah 2 + c = 0 cannot be satisfied by any real number; in this case, the equation is said to have twoimaginary root.

Example 5

Solve the equation:3x 2 – 27 = 0.

Solution: 3x 2 = 27; x 2 = 9; x =

Answer: x =

Example 6

Solve the equation:X 2 +25 = 0.

Solution: x 2 = - 25; x =
; imaginary roots.

Answer: x = + - 5 i.

b) To solve the equationOh 2 + bx = 0 , let's imagine it like thisX( ax + b ) = 0 . The product can be equal to zero only when any of the factors zero; therefore, the equation under consideration is satisfied if we assume thatx = 0 or ah + b = 0 /

The second equality gives
So the equationOh 2 + bx = 0 has two roots

x 1 = 0 and

Example 7

Solve the equation: 2x 2 - 7x = 0.

Solution: 2x 2 – 7x = 0, x(2x – 7) = 0; X 1=0; x 2 = .

Answer: x 1 \u003d 0; x 2 = .

in) Finally, the quadratic equationax 2 = 0 obviously has only one solution x = 0.

3. Particular cases of quadratic equations.

a) The case when the coefficienta very small.

Calculation of the roots of the equation ax 2 + bx + c= 0 according to the general formula derived above, it is difficult in this case, when the coefficienta very small number compared tob and with . Indeed, by calculating the roots by the formula

In most cases we must be content with the approximate value
, and hence the entire numerator. By dividing this approximate value by 2a, we thereby divide by 2a and the error with which the numerator of the formula was calculated. But since, according to the proposal, 2a is a very small fraction, dividing by a small fraction is tantamount to multiplying by a larger number, the error increases significantly, as a result of which the final result will be far from the true one. If, for example, 2a = 0.0001 and we calculated
to the fourth decimal place, then the margin of error in the final result will be 0.0001: 0.00001 = 10.

To calculate the roots of the equation in this case, a more convenient method of the so-calledsuccessive approximation.

Note that for a very small valuea one of the roots of the equation is slightly different from , and the other is a very large number (in absolute value). Indeed, the equation 2 + bx + c= 0 is equivalent to the equation

which can be given the appearance

As - a close to zero, then the last equation can be satisfied by such valuesX , for which one of the factors on the left side of the equation turns out to be a very small number, and the other is not very large; this will take place or when we giveX a very large absolute value, or whenX will be close to .

Let us show how to calculate one of the roots, which differs little from

(we find another root by subtracting the first from ).

From the equation we deduce
.

As a very small number andX and b not very large and not very small, then the absolute value of the fraction
very small. Neglecting this term, we get forx first approximation

Inserting this value into the right side of equation (1), we getsecond approximation, more accurate than the first one:

Inserting this quantity into the first part of equation (1), we obtainthird approximation , even more accurate. In a similar way, we can obtain, if necessary, the fourth and next approximation.

Example 8

Solve the equation: 0.003x 2 + 5x - 2 = 0

Decision:
.

First approximation = 0.4. This number is more true value of x 2 because we had to discardnegative member - 0.0006x 2.

Second approximation = 0.4 - 0.0006 (0.4) 2 = 0.399904. This number is less than the true valueX 2 number greater than x 2 , which causes the subtrahend to increase and the difference to decrease.

The third approximation would be greater than the true valueX , fourth less, etc.

Since 0.4 > x > 0.399904, instead of takingX one of these approximations, we will make an error less than 0.4 - 0.399904, i.e. less than 0.0001. Another root is obtained by subtracting the found root from
If we take the number 0.4 for the first root, then the other one is 1667, (6).

b) The case when with a very small number.

The method of successive approximation is also applicable when the free term of the equation is a very small number compared toa and b . In this case, one of the roots is close to
and the other is a very small amount. This is easy to verify if the equation is given the form

Since, according to the proposal, the absolute value iswith is very small, then the equation will obviously be satisfied whenX , or very close to 0, or very little different from

To find a root that has a very small value, we represent the equation again in the form

As a and b the essence of the numbers is not very large and not very small, but the absolute valueX 2 is very small, then for the first approximation we can neglect the term
; then we get
.

Inserting this value in placeX to the right side of equation (1), we obtain the second approximation; similarly, we find, if necessary, the following approximations.

4. Solving equations using the Vieta theorem

(direct and reverse).

The given quadratic equation has the form

Its roots satisfy the Vieta theorem, which, whena =1 has the form

a) If a free memberq of the given quadratic equation is positive, then the equation has two roots and this depends on the second coefficientp . If a p >0 , then both roots are negative ifp <0 , then both roots are positive.

Example 9

and

Example 10

and

b) If a free memberq of the above equation is negative, then the equation has two roots of different sign, and the larger root in absolute value will be positive ifp <0, or negative ifp >0 .

Example 11.

and

Example 12.

and

Example 13

Find the roots of the equation: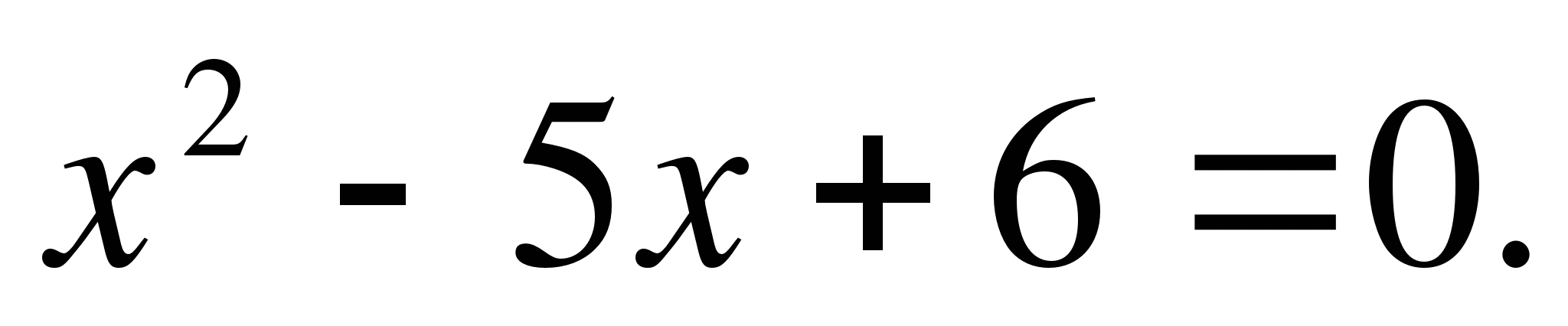

Solution: here p=-5, q=6. Pick two numbers x 1 and x 2 so that

According to Vieta's theorem

Answer:

5. Properties of the coefficients of a quadratic equation.

a) Let the quadratic equation be given

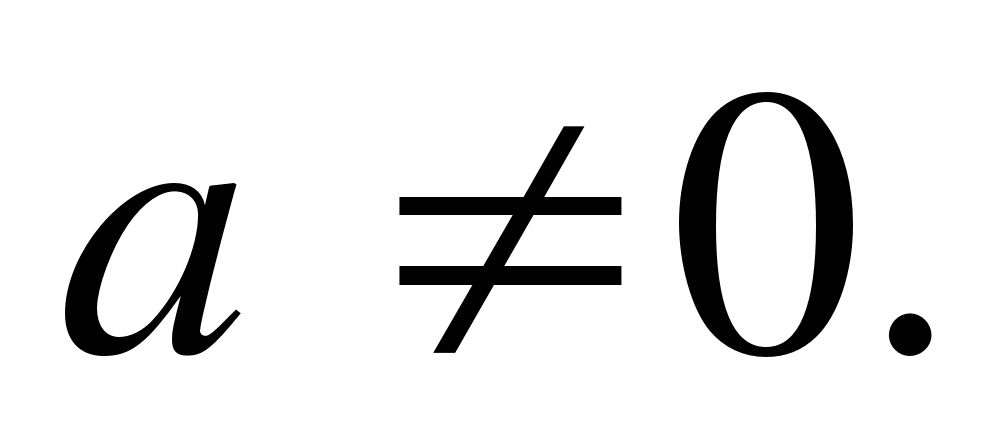
1. If a a + b + c \u003d 0 (i.e. the sum of the coefficients of the equation is zero), then

Proof: Divide both sides of the equation bya ≠ 0 , we obtain the reduced quadratic equation

According to Vieta's theorem

By condition a + b + c = 0, where c = - a - s. Means,

We get
Q.E.D.

2. If a a - b + c \u003d 0, or b \u003d a + c, then

Proof: According to Vieta's theorem

By condition a - c + c = 0, where c = a + c. Thus,

those.
Q.E.D.

3. If in the equation

Proof: Indeed, we present this equation in the form of the reduced

We write the equation in the form

The equation, written in this form, allows you to immediately get the roots

4. If a a = - c = m · n , in = m 2 – n 2 , then the roots have different signs, namely:

The signs in front of the fractions are determined by the sign of the second coefficient.

6. Solving equations using the "transfer" method.

Consider the quadratic equation

Oh 2 + b x + c= 0, and ≠ 0.

Multiplying both sides bya, we get the equation

a 2 X 2 + a b x + ac = 0.

Let be Oh= y, where from X = ; then we come to the equation

at 2 + by + ace = 0,

equivalent to this one.

its roots at 1 and at 2 find with the help of Vieta's theorem. Finally we get x 1 = them 1 = . With this method, the coefficienta is multiplied by the free term, as if “thrown” to it, which is why it is calledtransfer method. This method is used when it is easy to find the roots of an equation using Vieta's theorem and, most importantly, when the discriminant is an exact square.

Example 14

Solve the equation: 2x 2 - 11x + 15 = 0.

Solution: Let's "transfer" the coefficient 2 to the free term, as a result we get the equation:

at 2 – 11 y + 30 = 0.

According to Vieta's theorem

Answer: 2,5; 3.

7. Graphic solution quadratic equation.

If in the equation
move the second and third terms to the right side, we get

Let's build dependency graphs
and

The graph of the first dependence is a parabola passing through the origin. The graph of the second dependence is a straight line (Fig. 1).

The following cases are possible:

A straight line and a parabola can intersect at two points, the abscissas of the intersection points are the roots of a quadratic equation;

The line and the parabola can touch (only one common point), i.e. the equation has one solution;

The straight line and the parabola do not have common points, i.e. the quadratic equation has no real roots. Example 15

Solve the equation:2 x 2 + 6 x – 5 = 0.

Solution: Divide the equation into two parts:y = 2 x 2 and y = 6 x – 5.

Let's build an auxiliary table:

y = 2 x 2 -5

y = 6 x – 5

Let's build graphs of functionsy = 2 x 2 and y = 6 x – 5.

It can be seen from the graph that the two equations intersect at two pointsX 1 them 2 so the equation will have two rootsX 1 ≈ - 1.1 and x 2 ≈ 2,7.

Answer: x 1 ≈ - 1.1 and x 2 ≈ 2.7.

8. Solving quadratic equations with a compass and straightedge.

The graphical way to solve quadratic equations using a parabola is inconvenient.

If you build a parabola point by point, then it takes a lot of time, and the degree of accuracy of the results obtained is low.

We propose the following method for finding the roots of a quadratic equation

using a compass and a ruler (Fig. 5).

Let us assume that the desired circle intersects the axis

abscissa at points B(X 1 ;0) and D(X 2 ;0), where X 1 and X 2 are the roots of the equation
and passes through points A(0;1) and C
on the y-axis. Then by the theoremosecants we have OB OD= ОА OS, whence OS =

The center of the circle is at the point of intersection of the perpendicularsSF and SK, restored at the midpoints of the chords AC and BD,That's why

So:

1) build pointsS
(circle center) and A(0;1);

2) draw a circle with a radiusSA;

3) the abscissas of the points of intersection of this circle with the axis OX are the roots of the original quadratic equation.

In this case, three cases are possible.

1. The radius of the circle is greater than the ordinate of the center
circle intersects axis OX at two points (Fig. 6a) B(X 1 ;0) and D(X 2 ;0), where X 1 and X 2
1) The radius of the circle is greater than the ordinate of the center
circle intersects axis OX at two points (Fig. 6a) B(X 1 ;0) and D(X 2 ;0), where X 1 and X 2 are the roots of the quadratic equation

2. The radius of the circle is equal to the ordinate of the center
the circle touches the O axisX (Fig. 6,b) at point B(X 1 ;0), where X 1 is the root of the quadratic equation.

3. The radius of the circle is less than the ordinate of the center
the circle has no common points with the abscissa axis (Fig. 6,in ), in this case the equation has no solution.

a)
two rootsX 1 and X 2 .

b)
one rootX 1 .

in)
There are no real roots.

Example 16

Solve the equation:

Solution: see fig.7.

Determine the coordinates of the center of the circle by the formulas:

Let's draw a circle of radiusSA, where A (0; 1), S(1; -1).

Answer: -1; 3.

Example 17.

Solve the equation:
S see Bradis V.M (all in cm), from the similarity of triangles

Example 20.

For the equation

z 2 – 9 z + 8 = 0.

Nomogram gives roots

z 1 = 8, 0 and z 2 = 1, 0 (Fig. 12).

Solve with a nomogram

nomogram equation

2 z 2 – 9 z + 2 = 0.

Divide the coefficients of this

equations by 2, we get the equation

z 2 – 4, 5 + 1 = 0.

Nomogram gives rootsz 1 = 4 andz 2 = 0,5.

Example 21.

For the equation

z 2 + 5 z – 6 = 0

nomogram gives positive

rootz 1 = 1.0 and negative

find the root by subtracting

positive root

from– R, those. z 2 = – R - 1 =

= – 5 – 1 = – 6.0 (Fig.13.)

10. Geometric method for solving quadratic equations.

In ancient times, when geometry was more developed than algebra, quadratic equations were solved not algebraically, but geometrically. Let us give an example that has become famous from Algebra by al-Khwarizmi.

Example 22.

Solve the equation x 2 + 10x = 39.

In the original, this problem is formulated as follows: "A square and ten roots are equal to 39."

Solution: Consider a square with side x, rectangles are built on its sides so that the other side of each of them is 2, 2 = – 8.

y 3

at 2

Example 24.

Solve equations geometrically 2 – 6y – 16 = 0.

Transforming the equation, we get

at 2 - 6y \u003d 16.

On fig. find the "images" of the expression y 2 - 6y, i.e. from the area of a square with a sideat Subtract the area of a square with a side equal to 3 twice.

So, if the expression y 2 - 6y add 9, then we get the area of a square with side y - 3. Replacing the expression y 2 - 6y equal to it, we get: (y - 3) 2 = 16 +9, i.e. y – 3 = ±
or y - 3 = ± 5, where y 1 = 8 and y 2 = – 2.

y 3

y - 3

IV. CONCLUSION

As a result of this work, the following conclusions can be drawn:

The study of scientific and methodological literature on the topic of the work performed showed that the use of various methods for solving quadratic equations is an important link in the study of mathematics, increases interest, develops attention and ingenuity.

The system of using various methods of solving equations at different stages of the lesson is an effective means of activating students, has a positive effect on improving the quality of knowledge, skills, and develops mental activity.

The main thing in solving quadratic equations is to choose the right rational way of solving and apply the solution algorithm.

Work on this topic contributes to the further study of various ways of solving different equations.

v.LITERATURE

Great Soviet Encyclopedia.– M., Soviet Encyclopedia, 1974.

Newspaper "Mathematics".– Publishing house "First of September".

Glazer G.I. History of mathematics at school. 7-8 classes.– M., Education, 1982.

Children's encyclopedia. T. 2.– M., Pedagogy,1972.

Dorofeeva VA. Pages of history in mathematics lessons.– Lvov, Quantor,1991.

Liman M.M. Schoolchildren about mathematics and mathematicians.– M., Enlightenment,1981.

Encyclopedia for children.– M., Avanta +, 1997.

Alimov Sh.A., Ilyin V.A. et al. Algebra, 6-8. Trial textbook for grades 6-8 high school. – M., Enlightenment,1981. ;

Bradis V.M. Four-digit math tables for high school. Ed. 57th.– M., Enlightenment,1990. S. 83.

Zlotsky G.V. Task cards in teaching mathematics. The book for the teacher.– M., Education, 1992.

Klyukvin M.F. Algebra, 6-8. Student aid6-8 classes.– M., Education, 1963.

Kuzhepov A.K., Rubanov A.T. Algebra and elementary functions. Tutorial for secondary special educational institutions. – M., high school1969.

Mathematics (supplement to the newspaper "Pervoe september"), Nos. 21/96, 10/97, 24/97, 18/98, 21/98.

Okunev A.K.. Quadratic functions, equations and inequalities. A guide for the teacher.– M., Education, 1972.

Presman AA.Solving a quadratic equation with a compass and straightedge.– M., Kvant, No. 4/72. S. 34.

SolomnikB. C., Miloye P.I. Collection of questions and tasks in mathematics. Ed. 4th, add.– M., graduate School, 1973.

Khudobin A.I.. Collection of problems in algebra and elementary functions. A guide for the teacher. Ed. 2nd.– M., Education, 1970.

Lit.Pentkovsky M.V., Counting drawings. (Nomograms), 2nd ed., M., 1959;

Project
creative project name
Motto: In mathematics, little tricks play a big role.
Project author: Rylova Victoria
student of 8G class MOU secondary school No. 1
with in-depth study
individual items "Polyforum"

The main question of the project:
How varied are the solutions
quadratic equations?
Hypothesis:
I guess quadratic equations can be solved
in several different ways
Target:
The study of theoretical foundations and application on
practice different ways of solving square
equations

Tasks:
1. Pick up information on the topic from written
sources and the Internet
2. Synthesize information according to the plan
3. Explore different ways to solve square
equations and test the material in practice
Work plan:
Definition of the topic and purpose of the project,
formulation of the research topic
Determining the source of information
Determining how to collect and analyze
information
Determining the Presentation Method
results

annotation

Project "Methods for solving square
equations" reflects the results of the study,
conducted by me about what exist
ways to solve quadratic equations and what of
this you can take useful for yourself and mine
friends.
The theme of the project is related to using
ways to solve quadratic equations
find the unknown about the known.
Mathematics is taught in school
formulas for the roots of quadratic equations, with
which can be used to solve any
quadratic equations.
However, there are other solutions
equations that allow you to very quickly and
rationally solve quadratic equations.

From the history of square
equations
Quadratic equations have been solved for about 2000 years
BC e. Babylonians. Applying modern
algebraic notation, we can say that in their
cuneiform texts are found, except for incomplete ones, and
such as the complete quadratic equations:
Nearly all cuneiform writings found so far
texts give only problems with solutions,
stated in the form of prescriptions, without instructions
about how they were
found.

Indian scholar Brahmagupta (7th century),
outlined the general rule of thumb
quadratic equations reduced to
single canonical form:
ax2 + bx = c, a > 0
In the equation, the coefficients, except for a,
may be negative. rule
Brahmagupta is essentially the same as
ours.
Brahmagupta
Formulas for solving quadratic equations
were first published in a book
written by an Italian mathematician
Leonardo Fibonacci (XIII century). x2 + bx = c,
with all possible combinations of signs
coefficients b, c were
formulated in Europe only in 1544.
Leonardo Fibonacci

Only in the XVII century. thanks to the work of Girard, Descartes, Newton and
other scientists' way of solving quadratic equations
takes on a modern look.
I think
hence,
exist.
Descartes
There is a genius
thought patience,
concentrated
in famous
direction.
newton
All Equations
algebras have
so many decisions
how many
shows
Name
highest
quantities.
Girard
All mathematicians
knew that under
algebra were hidden
incomparable
treasure, but
were able to find them
viet

Geometric
solution way
square
equations
Decision
square
equations
via
nomograms
Decision
square
equations
using a circle
and rulers
Solutions
square
equations
way
"transfers"
Decomposition
left
parts of the equation
multipliers
Various
ways
solutions
square
equations
Graphic
decision
square
equations
Method
allocation
full square
Method
coefficients
Decision
square
equations
according to the formula
Decision
equations
using
Vieta's theorems

1. METHOD: Factoring the left side of the equation

Target:
give a quadratic equation
general view to view
A(x) B(x)=0,
where A(x) and B(x) -
polynomials with respect to x.
Ways:
Taking out the common factor for
parentheses;
Using formulas
abbreviated multiplication;
grouping method.
Let's solve the equation
x2 + 10x - 24 = 0.
Let's factorize the left side:
x2 + 10x - 24 =
\u003d (x + 12) (x - 2).
Hence,
(x + 12)(x - 2) = 0
Since the product is zero, then
one of its factors is equal to zero. Therefore the left side
The equation vanishes at x = 2, and also at x = - 12.
This means that the number 2 and - 12 are roots
equations x2 + 10x - 24 = 0.

2. METHOD: Full square selection method.

The essence of the method: bring a general quadratic equation to
incomplete quadratic equation.
Let's solve the equation x2 + 6x - 7 = 0.
Let's select a full square on the left side.
We now transform the left side of the equation
x2 + 6x - 7 = 0, adding to it and subtracting 9.
We have:
x2 + 6x - 7 =
\u003d x2 + 2 x 3 + 9 - 9 - 7 \u003d
\u003d (x + 3) 2 - 9 - 7 \u003d (x + 3) 2 - 16.
Thus, this equation can be written
So:
(x + 3) 2 - 16 \u003d 0,
(x + 3)2 = 16.
Therefore, x + 3 - 4 = 0, or x + 3 = -4
x1 = 1,
x2 = -7.

3. METHOD: Solving square
equations according to the formula
a 1
b 0, c 0
D>0
2 roots
D=0
1 root
x px g 0
2
D<0 Нет корней
Root formulas:
2
1
x1.2
p
2
b b 2 4ac
x1, 2
;
2a
2
p
g;
4
3
x1, 2
k k 2 ac
a

4. METHOD: Solving equations using the Vieta theorem.

As is known, the given quadratic equation has the form
x2 + px + c = 0. (1)
Its roots satisfy the Vieta theorem, which for a = 1 has the form
x1 x2 = q,
From this we can draw the following conclusions
x1 + x2 = -p
(from the coefficients p and q one can predict the signs
roots).
If (q > 0), then the equation has two identical
sign of the root, and this is the envy of the second coefficient p.
If p< 0, то оба корня отрицательны.
If p< 0, то оба корня положительны.

5. METHOD: Solving equations using the "transfer" method.

With this method, the coefficient a is multiplied by the free term, as if
"thrown" to him, so it is called the method of "transfer".
This method is used when it is easy to find the roots of the equation,
using the Vieta theorem and, most importantly, when the discriminant is
perfect square
Let's solve the equation 2x2 - 11x + 15 = 0.
Let's "throw" the coefficient 2 to the free term, in
as a result we get the equation
y2 - 11y + 30 = 0.
According to the Vieta theorem y \u003d 5, y \u003d 6, then x1 \u003d 5/2, x \u003d 6/2
Answer: 2.5; 3.

6. METHOD: Properties of the coefficients of a quadratic equation

Let the quadratic equation
ax2 + bx + c = 0, where a ≠ 0.
If, a + b + c \u003d 0, then
x1 1, x2
c
a
If b = a + c, then
x1 1, x2
c
a
1978x1984x60
2
x1 1;
6
x2
1978
319 x 2 1988 x 1669 0
x1 1;
1669
x2
.
319

7. METHOD: Graphical solution of a quadratic equation

transform the equation
x2 + px + q = 0
x2 = - px - q.
Let's build dependence graphs y \u003d x2 and y \u003d - px - q.
The graph of the first dependence is a parabola passing
through the origin. Schedule two
dependencies - straight line (Fig. 1). The following are possible
cases:
Direct and
parabola can
touch (only
one common
dot), i.e.
equation has
one solution;
straight and
parabola is not
have common points
those. square
the equation does not
roots.
straight line and parabola
may intersect in
two points, abscissa
points
intersections
are
roots
square
equations;

8. METHOD: Solving quadratic equations with a compass and ruler.

ax2 + bx + c = 0
So:
1) build points (circle center)
and A(0; 1);
2) draw a circle with a radius
SA;
3) the abscissas of the points of intersection of this
circles with the x-axis are
roots of the original square
equations.
2) the circle touches the x-axis in
In this case, three cases are possible.
1) the circle intersects the axis
Ox at two points
B(x1; 0) and D(x2; 0), where x1 and x2
- square roots
equations ax² + bx + c = 0.
point B(x1; 0), where x1 is the root
quadratic equation.
3) the circle has no common
points with the abscissa axis (Fig. 6, c), in
In this case, the equation does not
solutions.

9. METHOD: Solving quadratic equations using a nomogram.

Table XXII. p.83 (see Bradis V.M. Four-digit
mathematical tables. - M., Enlightenment,
1990).
Nomogram for Equation Solving
z2 + pz + q = 0. This nomogram allows,
without solving a quadratic equation,
determine the roots of the equation by its coefficients.
The curvilinear scale of the nomogram is built
according to the formulas (Fig. 11):
z2 + pz + q = 0,
where the letter z means the label of any
curved scale points.

10. METHOD: Geometrical way
solutions of quadratic equations.
How did the ancient Greeks solve
equation y2 + 6y - 16 = 0.
The solution is presented on
figure, where y2 + 6y = 16,
or y2 + 6 y + 9 = 16 + 9.
Expressions y2 + 6y + 9 and 16 + 9
geometrically represent
is the same square, and
original equation y2 + 6y - 16
+ 9 - 9 = 0 - the same
the equation. From where we get
that y + 3 = + 5 and y + 3 = -5, or
y=2, y2= -8
at
3
at
y2
3
3y
3y
9

my work makes it possible
look at the challenges that
we have mathematics.
these solutions deserve
attention
because they are not reflected in
school textbooks of mathematics;
mastering these techniques helps me
save time and solve efficiently
equations;
need for a quick solution
due to the use of a test system
final exams;

Conclusion

“In mathematics, one must remember not
formulas, but processes of thought"
V.P. Ermakov

Kopyevskaya rural secondary school

10 Ways to Solve Quadratic Equations

Head: Patrikeeva Galina Anatolyevna,

mathematic teacher

s.Kopyevo, 2007

1. History of the development of quadratic equations

1.1 Quadratic equations in ancient Babylon

1.2 How Diophantus compiled and solved quadratic equations

1.3 Quadratic equations in India

1.4 Quadratic equations in al-Khwarizmi

1.5 Quadratic equations in Europe XIII - XVII centuries

1.6 About Vieta's theorem

2. Methods for solving quadratic equations

Conclusion

Literature

1. History of the development of quadratic equations

1.1 Quadratic equations in ancient Babylon

The need to solve equations not only of the first, but also of the second degree in ancient times was caused by the need to solve problems related to finding the areas of land and earthworks of a military nature, as well as the development of astronomy and mathematics itself. Quadratic equations were able to solve about 2000 BC. e. Babylonians.

Applying modern algebraic notation, we can say that in their cuneiform texts there are, in addition to incomplete ones, such, for example, complete quadratic equations:

X2 + X= ¾; X2 - X= 14,5

The rule for solving these equations, stated in the Babylonian texts, coincides essentially with the modern one, but it is not known how the Babylonians came to this rule. Almost all the cuneiform texts found so far give only problems with solutions stated in the form of recipes, with no indication of how they were found.

Despite the high level of development of algebra in Babylon, the cuneiform texts lack the concept of a negative number and general methods for solving quadratic equations.

1.2 How Diophantus compiled and solved quadratic equations.

Diophantus' Arithmetic does not contain a systematic exposition of algebra, but it contains a systematic series of problems, accompanied by explanations and solved by formulating equations of various degrees.

When compiling equations, Diophantus skillfully chooses unknowns to simplify the solution.

Here, for example, is one of his tasks.

Task 11."Find two numbers knowing that their sum is 20 and their product is 96"

Diophantus argues as follows: it follows from the condition of the problem that the desired numbers are not equal, since if they were equal, then their product would be equal not to 96, but to 100. Thus, one of them will be more than half of their sum, i.e. . 10+x, the other is smaller, i.e. 10's. The difference between them 2x.

Hence the equation:

(10 + x)(10 - x) = 96

100's 2 = 96

X 2 - 4 = 0 (1)

From here x = 2. One of the desired numbers is 12 , other 8 . Decision x = -2 for Diophantus does not exist, since Greek mathematics knew only positive numbers.

If we solve this problem by choosing one of the desired numbers as the unknown, then we will come to the solution of the equation

y(20 - y) = 96,

at2 - 20y + 96 = 0. (2)

It is clear that, by choosing the half-difference of the desired numbers as the unknown, Diophantus simplifies the solution; he manages to reduce the problem to solving an incomplete quadratic equation (1).

1.3 Quadratic equations in India

Problems for quadratic equations are already found in the astronomical tract "Aryabhattam", compiled in 499 by the Indian mathematician and astronomer Aryabhatta. Another Indian scientist, Brahmagupta (7th century), outlined the general rule for solving quadratic equations reduced to a single canonical form:

Oh2 + bx = c, a > 0. (1)

In equation (1), the coefficients, except for a, can also be negative. Brahmagupta's rule essentially coincides with ours.

In ancient India, public competitions in solving difficult problems were common. In one of the old Indian books, the following is said about such competitions: “As the sun outshines the stars with its brilliance, so a learned person will outshine the glory of another in public meetings, proposing and solving algebraic problems.” Tasks were often dressed in poetic form.

Here is one of the problems of the famous Indian mathematician of the XII century. Bhaskara.

Task 13.

“A frisky flock of monkeys And twelve in vines ...

Having eaten power, had fun. They began to jump, hanging ...

Part eight of them in a square How many monkeys were there,

Having fun in the meadow. You tell me, in this flock?

Bhaskara's solution indicates that he knew about the two-valuedness of the roots of quadratic equations (Fig. 3).

The equation corresponding to problem 13 is:

(x/8) 2 + 12 = x

Bhaskara writes under the guise of:

X2 - 64x = -768

and, to complete the left side of this equation to a square, he adds to both sides 32 2 , getting then:

X2 - 64x + 322 = -768 + 1024,

(x - 32)2 = 256,

x - 32 = ± 16,

X1 = 16, x2 = 48.

1.4 Quadratic equations in al-Khorezmi

Al-Khorezmi's algebraic treatise gives a classification of linear and quadratic equations. The author lists 6 types of equations, expressing them as follows:

1) "Squares are equal to roots", i.e. Oh2 + with =bX.

2) "Squares are equal to number", i.e. Oh2 = s.

3) "The roots are equal to the number", i.e. ah = s.

4) "Squares and numbers are equal to roots", i.e. Oh2 + with =bX.

5) "Squares and roots are equal to the number", i.e. Oh2 + bx= s.

6) "Roots and numbers are equal to squares", i.e.bx+ c = ax2 .

For al-Khwarizmi, who avoided the use of negative numbers, the terms of each of these equations are addends, not subtractions. In this case, equations that do not have positive solutions are obviously not taken into account. The author outlines the methods for solving these equations, using the methods of al-jabr and al-muqabala. His decisions, of course, do not completely coincide with ours. Not to mention the fact that it is purely rhetorical, it should be noted, for example, that when solving an incomplete quadratic equation of the first type

al-Khorezmi, like all mathematicians before the 17th century, does not take into account the zero solution, probably because it does not matter in specific practical problems. When solving the complete quadratic equations of al - Khorezmi on partial numerical examples sets out the decision rules, and then the geometric proofs.

Task 14.“The square and the number 21 are equal to 10 roots. Find the root" (assuming the root of the equation x2 + 21 = 10x).

The author's solution goes something like this: divide the number of roots in half, you get 5, multiply 5 by itself, subtract 21 from the product, 4 remains. Take the root of 4, you get 2. Subtract 2 from 5, you get 3, this will be the desired root. Or add 2 to 5, which will give 7, this is also a root.

Treatise al - Khorezmi is the first book that has come down to us, in which the classification of quadratic equations is systematically stated and formulas for their solution are given.

1.5 Quadratic equations in EuropeXIII- XVIIcenturies

Formulas for solving quadratic equations on the model of al - Khorezmi in Europe were first set forth in the "Book of the Abacus", written in 1202 by the Italian mathematician Leonardo Fibonacci. This voluminous work, which reflects the influence of mathematics, both the countries of Islam and Ancient Greece, differs in both completeness and clarity of presentation. The author independently developed some new algebraic examples of problem solving and was the first in Europe to approach the introduction of negative numbers. His book contributed to the spread of algebraic knowledge not only in Italy, but also in Germany, France and other European countries. Many tasks from the "Book of the Abacus" passed into almost all European textbooks of the 16th - 17th centuries. and partly XVIII.

PAGE_BREAK--

The general rule for solving quadratic equations reduced to a single canonical form:

X2 + bx= with,

for all possible combinations of signs of the coefficients b, with was formulated in Europe only in 1544 by M. Stiefel.

Vieta has a general derivation of the formula for solving a quadratic equation, but Vieta recognized only positive roots. The Italian mathematicians Tartaglia, Cardano, Bombelli were among the first in the 16th century. Take into account, in addition to positive, and negative roots. Only in the XVII century. Thanks to the work of Girard, Descartes, Newton and other scientists, the way to solve quadratic equations takes on a modern look.

1.6 About Vieta's theorem

The theorem expressing the relationship between the coefficients of a quadratic equation and its roots, bearing the name of Vieta, was formulated by him for the first time in 1591 as follows: “If B+ D multiplied by A- A2 , equals BD, then A equals AT and equal D».

To understand Vieta, one must remember that BUT, like any vowel, meant for him the unknown (our X), the vowels AT,D- coefficients for the unknown. In the language of modern algebra, Vieta's formulation above means: if

(a +b)x - x2 = ab,

X2 - (a +b)x + ab= 0,

X1 = a, x2 = b.

Expressing the relationship between the roots and coefficients of the equations general formulas, written using symbols, Viet established uniformity in the methods of solving equations. However, the symbolism of Vieta is still far from modern look. He did not recognize negative numbers, and therefore, when solving equations, he considered only cases where all roots are positive.

2. Methods for solving quadratic equations

Quadratic equations are the foundation on which the majestic edifice of algebra rests. Quadratic equations are widely used in solving trigonometric, exponential, logarithmic, irrational and transcendental equations and inequalities. We all know how to solve quadratic equations from school (grade 8) until graduation.

In the school course of mathematics, the formulas of the roots of quadratic equations are studied, with the help of which you can solve any quadratic equations. However, there are other ways to solve quadratic equations that allow you to solve many equations very quickly and rationally. There are ten ways to solve quadratic equations. In my work, I analyzed each of them in detail.

1. METHOD : Factorization of the left side of the equation.

Let's solve the equation

X2 + 10x - 24 = 0.

Let's factorize the left side:

X2 + 10x - 24 = x2 + 12x - 2x - 24 \u003d x (x + 12) - 2 (x + 12) \u003d (x + 12) (x - 2).

Therefore, the equation can be rewritten as:

(x + 12)(x - 2) = 0

Since the product is zero, then at least one of its factors is zero. Therefore, the left side of the equation vanishes at x = 2, as well as at x = - 12. This means that the number 2 and - 12 are the roots of the equation X2 + 10x - 24 = 0.

2. METHOD : Full square selection method.

Let's solve the equation X2 + 6x - 7 = 0.

Let's select a full square on the left side.

To do this, we write the expression x2 + 6x in the following form:

X2 + 6x = x2 + 2 x 3.

In the resulting expression, the first term is the square of the number x, and the second is the double product of x by 3. Therefore, to get the full square, you need to add 32, since

x2 + 2 x 3 + 32 = (x + 3)2 .

We now transform the left side of the equation

X2 + 6x - 7 = 0,

adding to it and subtracting 32. We have:

X2 + 6x - 7 = x2 + 2 x 3 + 32 - 3 2 - 7 = (x + 3)2 - 9 - 7 = (x + 3)2 - 16.

Thus, this equation can be written as follows:

(x + 3)2 - 16 = 0, (x + 3)2 = 16.

Hence, x + 3 - 4 = 0, x1 = 1, or x + 3 = -4, x2 = -7.

3. METHOD :Solution of quadratic equations by formula.

Multiply both sides of the equation

Oh2 + bx + c = 0, a ≠ 0

on 4a and successively we have:

4a2 X2 + 4abx + 4ac = 0,

((2ah)2 + 2axb+ b2 ) - b2 + 4 ac= 0,

(2ax+b)2 = b2 - 4ac,

2ax + b = ± √ b2 - 4ac,

2ax = - b ± √ b2 - 4ac,

Examples.

a) Let's solve the equation: 4x2 + 7x + 3 = 0.

a = 4,b= 7, c = 3,D= b2 - 4 ac= 7 2 - 4 4 3 = 49 - 48 = 1,

D> 0, two different roots;

Thus, in the case of a positive discriminant, i.e. at

b2 - 4 ac>0 , the equation Oh2 + bx + c = 0 has two different roots.

b) Let's solve the equation: 4x2 - 4x + 1 = 0,

a = 4,b= - 4, c = 1,D= b2 - 4 ac= (-4) 2 - 4 4 1= 16 - 16 = 0,

D= 0, one root;

So, if the discriminant is zero, i.e. b2 - 4 ac= 0 , then the equation

Oh2 + bx + c = 0 has a single root

in) Let's solve the equation: 2x2 + 3x + 4 = 0,

a = 2,b= 3, c = 4,D= b2 - 4 ac= 3 2 - 4 2 4 = 9 - 32 = - 13, D< 0.

Continuation
--PAGE_BREAK--

This equation has no roots.

So, if the discriminant is negative, i.e. b2 - 4 ac< 0 ,

the equation Oh2 + bx + c = 0 has no roots.

Formula (1) of the roots of the quadratic equation Oh2 + bx + c = 0 allows you to find the roots any quadratic equation (if any), including reduced and incomplete. Formula (1) is expressed verbally as follows: the roots of a quadratic equation are equal to a fraction whose numerator is equal to the second coefficient, taken with the opposite sign, plus minus the square root of the square of this coefficient without quadruple the product of the first coefficient by the free term, and the denominator is twice the first coefficient.

4. METHOD: Solution of equations using Vieta's theorem.

As is known, the given quadratic equation has the form

X2 + px+ c= 0. (1)

Its roots satisfy the Vieta theorem, which, when a =1 has the form

/>x1 x2 = q,

x1 + x2 = - p

From this we can draw the following conclusions (the signs of the roots can be predicted from the coefficients p and q).

a) If the summary term q of the reduced equation (1) is positive ( q> 0 ), then the equation has two roots of the same sign and this is the envy of the second coefficient p. If a R< 0 , then both roots are negative if R< 0 , then both roots are positive.

For example,

x2 – 3 x+ 2 = 0; x1 = 2 and x2 = 1, as q= 2 > 0 and p= - 3 < 0;

x2 + 8 x+ 7 = 0; x1 = - 7 and x2 = - 1, as q= 7 > 0 and p= 8 > 0.

b) If a free member q of the reduced equation (1) is negative ( q< 0 ), then the equation has two roots of different sign, and the larger root in absolute value will be positive if p< 0 , or negative if p> 0 .

For example,

x2 + 4 x– 5 = 0; x1 = - 5 and x2 = 1, as q= - 5 < 0 and p= 4 > 0;

x2 – 8 x– 9 = 0; x1 = 9 and x2 = - 1, as q= - 9 < 0 and p= - 8 < 0.

5. METHOD: Solving equations using the "transfer" method.

Consider the quadratic equation

Oh2 + bx + c = 0, where a ≠ 0.

Multiplying both its parts by a, we obtain the equation

a2 X2 + abx + ac = 0.

Let be ah = y, where x = y/a; then we come to the equation

at2 + by+ ac = 0,

equivalent to this one. its roots at1 and at 2 can be found using Vieta's theorem.

Finally we get

X1 = y1 /a and X1 = y2 /a.

With this method, the coefficient a is multiplied by the free term, as if “thrown” to it, therefore it is called transfer method. This method is used when it is easy to find the roots of an equation using Vieta's theorem and, most importantly, when the discriminant is an exact square.

Example.

Let's solve the equation 2x2 – 11x + 15 = 0.

Decision. Let's "transfer" the coefficient 2 to the free term, as a result we get the equation

at2 – 11y + 30 = 0.

According to Vieta's theorem

/>/>/>/>/>at1 = 5 x1 = 5/2 x1 = 2,5

at2 = 6 x2 = 6/2 x2 = 3.

Answer: 2.5; 3.

6. METHOD: Properties of the coefficients of a quadratic equation.

BUT. Let the quadratic equation

Oh2 + bx + c = 0, where a ≠ 0.

1) If, a+b+ c = 0 (i.e. the sum of the coefficients is zero), then x1 = 1,

X2 = s/a.

Proof. We divide both sides of the equation by a ≠ 0, we get the reduced quadratic equation

x2 + b/ a x+ c/ a= 0.

/>According to Vieta's theorem

x1 + x2 = - b/ a,

x1 x2 = 1 c/ a.

By condition a -b+ c = 0, where b= a + c. Thus,

/>x1 + x2 = - a+ b / a \u003d -1 - c / a,

x1 x2 = - 1 (-c/a),

those. X1 = -1 and X2 = c/ a, which we needed to prove.

Examples.

Let's solve the equation 345x2 - 137x - 208 = 0.

Decision. As a +b+ c \u003d 0 (345 - 137 - 208 \u003d 0), then

X1 = 1, x2 = c/ a= -208/345.

Answer: 1; -208/345.

2) Solve the equation 132x2 – 247x + 115 = 0.

Decision. As a +b+ c \u003d 0 (132 - 247 + 115 \u003d 0), then

X1 = 1, x2 = c/ a= 115/132.

Answer: 1; 115/132.

B. If the second coefficient b= 2 k– even number, then the formula of the roots

Continuation
--PAGE_BREAK--

Example.

Let's solve the equation 3x2 - 14x + 16 = 0.

Decision. We have: a = 3,b= - 14, c = 16,k= - 7 ;

D= k2 – ac= (- 7) 2 – 3 16 = 49 – 48 = 1, D> 0, two different roots;

Answer: 2; 8/3

AT. Reduced Equation

X2 +px+q= 0

coincides with the general equation, in which a = 1, b= p and c =q. Therefore, for the reduced quadratic equation, the formula for the roots

takes the form:

Formula (3) is especially convenient to use when R- even number.

Example. Let's solve the equation X2 – 14x – 15 = 0.

Decision. We have: X1,2 =7±

Answer: x1 = 15; X2 = -1.

7. METHOD: Graphical solution of a quadratic equation.

If in the equation

X2 + px+ q= 0

move the second and third terms to the right side, we get

X2 = - px- q.

Let's build dependence graphs y \u003d x2 and y \u003d - px - q.

The graph of the first dependence is a parabola passing through the origin. Graph of the second dependency -

straight line (Fig. 1). The following cases are possible:

A straight line and a parabola can intersect at two points, the abscissas of the intersection points are the roots of a quadratic equation;

The line and the parabola can touch (only one common point), i.e. the equation has one solution;

The straight line and the parabola do not have common points, i.e. a quadratic equation has no roots.

Examples.

1) Let's solve the equation graphically X2 - 3x - 4 = 0(Fig. 2).

Decision. We write the equation in the form X2 = 3x + 4.

Let's build a parabola y = x2 and direct y = 3x + 4. direct

y = 3x + 4 can be built from two points M (0; 4) and

N(3; 13) . A line and a parabola intersect at two points

BUT and AT with abscissa X1 = - 1 and X2 = 4 . Answer : X1 = - 1;

X2 = 4.

2) Let's solve the equation graphically (Fig. 3) X2 - 2x + 1 = 0.

Decision. We write the equation in the form X2 = 2x - 1.

Let's build a parabola y = x2 and direct y = 2x - 1.

direct y = 2x - 1 build on two points M (0; - 1)

and N(1/2; 0) . Line and parabola intersect at a point BUT with

abscissa x = 1. Answer: x = 1.

3) Let's solve the equation graphically X2 - 2x + 5 = 0(Fig. 4).

Decision. We write the equation in the form X2 = 5x - 5. Let's build a parabola y = x2 and direct y = 2x - 5. direct y = 2x - 5 construct by two points M(0; - 5) and N(2.5; 0). The straight line and the parabola have no intersection points, i.e. This equation has no roots.

Answer. The equation X2 - 2x + 5 = 0 has no roots.

8. METHOD: Solving quadratic equations with a compass and straightedge.

The graphical way to solve quadratic equations using a parabola is inconvenient. If you build a parabola point by point, then it takes a lot of time, and the degree of accuracy of the results obtained is low.

I propose the following method for finding the roots of a quadratic equation Oh2 + bx + c = 0 using a compass and ruler (Fig. 5).

Let us assume that the desired circle intersects the axis

abscissa in points B(x1 ; 0) and D(X2 ; 0), where X1 and X2 - roots of the equation Oh2 + bx + c = 0, and passes through the points

A(0; 1) and C(0;c/ a) on the y-axis. Then, by the secant theorem, we have OB OD= OA OC, where OC= OB OD/ OA= x1 X2 / 1 = c/ a.

The center of the circle is at the point of intersection of the perpendiculars SF and SK, restored at the midpoints of the chords AC and BD, That's why

1) construct points (the center of the circle) and A(0; 1) ;

2) draw a circle with a radius SA;

3) the abscissas of the points of intersection of this circle with the axis Oh are the roots of the original quadratic equation.

In this case, three cases are possible.

1) The radius of the circle is greater than the ordinate of the center (AS> SK, orR> a+ c/2 a) , the circle intersects the x-axis at two points (Fig. 6, a) B(x1 ; 0) and D(X2 ; 0) , where X1 and X2 - roots of the quadratic equation Oh2 + bx + c = 0.

2) The radius of the circle is equal to the ordinate of the center (AS= SB, orR= a+ c/2 a) , the circle touches the Ox axis (Fig. 6, b) at the point B(x1 ; 0) , where x1 is the root of the quadratic equation.

Continuation
--PAGE_BREAK--

3) The radius of the circle is less than the ordinate of the center, the circle has no common points with the abscissa axis (Fig. 6, c), in this case the equation has no solution.

Example.

Let's solve the equation X2 - 2x - 3 = 0(Fig. 7).

Decision. Determine the coordinates of the point of the center of the circle by the formulas:

Let's draw a circle of radius SA, where A (0; 1).

Answer:X1 = - 1; X2 = 3.

9. METHOD: Solving quadratic equations using a nomogram.

This is an old and undeservedly forgotten method for solving quadratic equations, placed on p. 83 (see Bradis V.M. Four-valued mathematical tables. - M., Enlightenment, 1990).

Table XXII. Nomogram for Equation Solving z2 + pz+ q= 0 . This nomogram allows, without solving the quadratic equation, to determine the roots of the equation by its coefficients.

The curvilinear scale of the nomogram is built according to the formulas (Fig. 11):

Assuming OS = p,ED= q, OE = a(all in cm), from the similarity of triangles SAN and CDF we get the proportion

whence, after substitutions and simplifications, the equation follows

z2 + pz+ q= 0,

and the letter z means the label of any point on the curved scale.

Examples.

1) For the equation z2 - 9 z+ 8 = 0 nomogram gives roots

z1 = 8,0 and z2 = 1,0 (Fig. 12).

2) We solve the equation using the nomogram

2 z2 - 9 z+ 2 = 0.

We divide the coefficients of this equation by 2, we get the equation

z2 - 4,5 z+ 1 = 0.

Nomogram gives roots z1 = 4 and z2 = 0,5.

3) For the equation

z2 - 25 z+ 66 = 0

coefficients p and q are out of scale, we will perform the substitution z= 5 t, we get the equation

t2 - 5 t+ 2,64 = 0,

which we solve by means of a nomogram and get t1 = 0,6 and t2 = 4,4, where z1 = 5 t1 = 3,0 and z2 = 5 t2 = 22,0.

10. METHOD: Geometric way of solving quadratic equations.

In ancient times, when geometry was more developed than algebra, quadratic equations were solved not algebraically, but geometrically. I will give an example that has become famous from the "Algebra" of al-Khwarizmi.

Examples.

1) Solve the equation X2 + 10x = 39.

In the original, this problem is formulated as follows: “The square and ten roots are equal to 39” (Fig. 15).

Decision. Consider a square with side x, rectangles are built on its sides so that the other side of each of them is 2.5, therefore, the area of \u200b\u200beach is 2.5x. The resulting figure is then supplemented to a new square ABCD, completing four equal squares in the corners, the side of each of them is 2.5, and the area is 6.25.

Square S square ABCD can be represented as the sum of the areas: the original square X2 , four rectangles (4 2.5x = 10x) and four attached squares (6,25 4 = 25) , i.e. S= X2 + 10x + 25. Replacing

X2 + 10x number 39 , we get that S= 39 + 25 = 64 , whence it follows that the side of the square ABCD, i.e. line segment AB = 8. For the desired side X the original square we get

2) But, for example, how the ancient Greeks solved the equation at2 + 6y - 16 = 0.

Decision shown in fig. 16, where

at2 + 6y = 16, or y2 + 6y + 9 = 16 + 9.

Decision. Expressions at2 + 6y + 9 and 16 + 9 geometrically represent the same square, and the original equation at2 + 6y - 16 + 9 - 9 = 0 is the same equation. From where we get that y + 3 = ± 5, or at1 = 2, y2 = - 8 (Fig. 16).

3) Solve geometric equation at2 - 6y - 16 = 0.

Transforming the equation, we get

at2 - 6y = 16.

On fig. 17 find the "images" of the expression at2 - 6u, those. from the area of a square with side y subtract twice the area of a square with side equal to 3 . So, if the expression at2 - 6y add 9 , then we get the area of a square with a side y - 3. Replacing the expression at2 - 6y its equal number 16,

we get: (y - 3)2 = 16 + 9, those. y - 3 = ± √25, or y - 3 = ± 5, where at1 = 8 and at2 = - 2.

Conclusion

Quadratic equations are widely used in solving trigonometric, exponential, logarithmic, irrational and transcendental equations and inequalities.

However, the value of quadratic equations lies not only in the elegance and brevity of solving problems, although this is very significant. No less important is the fact that as a result of the use of quadratic equations in solving problems, new details are often discovered, interesting generalizations can be made and refinements made, which are prompted by an analysis of the obtained formulas and relations.

I would also like to note that the topic presented in this work is still little studied at all, they just do not deal with it, therefore it is fraught with a lot of hidden and unknown, which provides an excellent opportunity for further work above her.

Here I settled on the question of solving quadratic equations, and what,

if there are other ways to solve them?! Again, find beautiful patterns, some facts, clarifications, make generalizations, discover everything new and new. But these are questions for future works.

Summing up, we can conclude: quadratic equations play a huge role in the development of mathematics. We all know how to solve quadratic equations from school (grade 8) until graduation. This knowledge can be useful to us throughout life.

Since these methods for solving quadratic equations are easy to use, they should certainly be of interest to students who are fond of mathematics. My work makes it possible to take a different look at the problems that mathematics sets before us.

Literature:

1. Alimov Sh.A., Ilyin V.A. et al. Algebra, 6-8. Trial textbook for 6-8 grade high school. - M., Education, 1981.

2. Bradis V.M. Four-digit mathematical tables for high school. Ed. 57th. - M., Education, 1990. S. 83.

3. Kruzhepov A.K., Rubanov A.T. Problem book on algebra and elementary functions. Textbook for secondary specialized educational institutions. - M., higher school, 1969.

4. Okunev A.K. Quadratic functions, equations and inequalities. A guide for the teacher. - M., Education, 1972.

5. Presman A.A. Solving a quadratic equation with a compass and straightedge. - M., Kvant, No. 4/72. S. 34.

6. Solomnik V.S., Milov P.I. Collection of questions and tasks in mathematics. Ed. - 4th, add. - M., Higher School, 1973.

7. Khudobin A.I. Collection of problems in algebra and elementary functions. A guide for the teacher. Ed. 2nd. - M., Education, 1970.

https://pandia.ru/text/78/082/images/image002_237.gif" height="952"> MOU "Sergievskaya Secondary School"

Completed by: Sizikov Stanislav

Teacher:

with. Sergievka, 2007

1. Introduction. Quadratic Equations in Ancient Babylon……………….3

2. Quadratic equations in Diaphant…………..………………………….4

3. Quadratic equations in India …………………………………………………………………………………………………………………………………………………………………………………………

4. Quadratic equations in al-Khorezmi …………………………………..6

5. Quadratic equations in Europe XIII - XYII…………………………...7

6. About the Vieta theorem …………………………………………………………..9

7. Ten ways to solve quadratic equations……………………..10

8. Conclusion …………………………………………………………………20

9. References ……………………………………………………...21

Introduction

Quadratic equations

Quadratic equations are the foundation on which the majestic edifice of algebra rests. Quadratic equations are widely used in solving trigonometric, exponential, logarithmic, irrational equations. We all know how to solve quadratic equations, starting from grade 8. But how did the history of solving quadratic equations originate and develop?

Quadratic Equations in Ancient Babylon

The need to solve equations not only of the first, but also of the second degree, back in antiquity, was caused by the need to solve problems related to finding the areas of land; earthworks of a military nature, as well as with the development of astronomy and mathematics itself. Quadratic equations were able to solve about 2000 BC. e. Babylonians. Using modern algebraic notation, we can say that in their cuneiform texts there are, in addition to incomplete ones, such, for example, complete quadratic equations: x2 + x = , : x2 - x = 14https://pandia.ru/text/78/082 /images/image005_150.gif" width="16" height="41 src=">)2 + 12 = x; Bhaskara writes under the guise

x2- 64X = - 768

and, to complete the left side of this equation to the square, he adds 322 to both sides, getting then: x2- 64x + 322 = - 768 + 1024;

(X- 32)2 = 256; X - 32 = ± 16, xt = 16, hg= 48.

Quadratic equations in al - Khorezmi

Al-Khwarizmi's algebraic treatise gives a classification of linear and quadratic equations. The author lists 6 types of equations, expressing them as follows:

1) "Squares are equal to roots", i.e. ax2 = in.

2) “Squares are equal to number”, i.e. ah2= with.

3) "The roots are equal to the number", i.e. ah = s.

4) “Squares and numbers are equal to roots”, i.e. ah2+ c = in.

5) “Squares and roots are equal to number”, i.e. ah2+ in = s.

6) "Roots and numbers are equal to squares", i.e. in+ c \u003d ax2. For al-Khwarizmi, who avoided the use of negative numbers, the terms of each of these equations are addends, not subtractions. In this case, equations that do not have positive solutions are obviously not taken into account. The author sets out methods for solving these equations. His decision, of course, does not completely coincide with ours. Not to mention the fact that it is purely rhetorical, it should be noted, for example, that when solving an incomplete quadratic equation of the first type, al-Khwarizmi, like all mathematicians before the 17th century, does not take into account the zero solution, probably because in specific practical tasks, it does not matter. When solving complete quadratic equations, al-Khwarizmi sets out the rules for solving them using particular numerical examples, and then their geometric proofs.

Let's take an example.

Problem 14. “The square and the number 21 are equal to 10 roots. Find the root "(meaning the root of the equation x2+ 21 = 10X).

The treatise of al-Khwarizmi is the first book that has come down to us, in which the classification of quadratic equations is systematically presented and formulas for their solution are given.

Quadratic equations in EuropeXIII- XVIIcenturies

The formulas for solving quadratic equations on the model of al-Khwarizmi in Europe were first set forth in the Book of the Abacus (published in Rome in the middle of the last century, the Fibonacci Book of the Abacus contains 459 pages), written in 1202 by the Italian mathematician Leonardo Fibonacci. This voluminous work, which reflects the influence of mathematics from both the countries of Islam and Ancient Greece, is distinguished by both completeness and clarity of presentation. The author independently developed some new algebraic examples of problem solving and the first in Europe approached the introduction of negative numbers. His book contributed to the spread of algebraic knowledge not only in Italy, but also in Germany, France and other European countries. Many tasks from the Book of the Abacus passed into almost all European textbooks of the 16th-17th centuries. and partly XVIII.

General rule for solving quadratic equations reduced to a single canonical form x2+ in = s, for all possible combinations of signs of the coefficients in, with was formulated in Europe only in 1544. M. Stiefel.

Vieta has a general derivation of the formula for solving a quadratic equation, but Vieta recognized only positive roots. The Italian mathematicians Tartaglia, Cardaco, Bombelli were among the first in the 16th century. take into account, in addition to positive, and negative roots. Only in the XVII century. thanks to the works of Girard, Descartes, Newton and other scientists, the method of solving quadratic equations takes on a modern look.

About Vieta's theorem

The theorem expressing the relationship between the coefficients of a quadratic equation and its roots, bearing the name of Vieta, was formulated by him for the first time in 1591 as follows: “If AT+ D, multiplied by BUT minus A2, equals BD, then BUT equals AT and equal D».

To understand Vieta, one must remember that BUT, like any
vowel, meant for him unknown (our X), vowels
AT,D- coefficients for the unknown. In the language of modern algebra, Vieta's formulation above means: if

(a+ c) x - x 2 = ab, x2 - (a+ b) x + ab = 0, x1 = a, x2 = b.

Expressing the relationship between the roots and coefficients of equations by general formulas written using symbols, Viet established uniformity in the methods of solving equations. However, the symbolism of Vieta is still far from its modern form. He did not recognize negative numbers and therefore, when solving equations, he considered only cases where all roots are positive.

Ten Ways to Solve Quadratic Equations

1. Factorization of the left side of the equation

Let's solve the equation x2+ 10X- 24 = 0. Let's factorize the left side of the equation:

x2 + 10x - 24 = x2 + 12x - 2x - 24 =

X(x + x + 12) = (x + 12)(x - 2).

Therefore, the equation can be rewritten as:

( X + 12)(x - 2) = 0.

Since the product is zero, at least one of its factors is zero. Therefore, the left side of the equation vanishes when x = 2, as well as X= - 12. This means that the numbers 2 and - 12 are the roots of the equation x2 + 10x - 24 = 0.

2. Full square selection method

Let's explain this method with an example.

Let's solve the equation x2 + 6x - 7 = 0. Select a full square on the left side. To do this, we write the expression x2 + 6x in the following form:

x2 + 6x = x2 + 2*x*3.

In the resulting expression, the first term is the square of the number x, and the second is the double product of x by 3. Therefore, to get the full square, you need to add 32, since

x2 + 2 x 3 + 32 = (x + 3)2.

We now transform the left side of the equation

x2 + 6x - 7 = 0,

adding to it and subtracting 32. We have:

x2 + 6x - 7 = x2 + 2 X 3 +– 7 = (X- \u003d (x - Z) 2 - 16 .

Thus, this equation can be written as follows:

(x + = 0, i.e. (x + 3)2 = 16.

Hence, X+ 3 \u003d 4 x1 \u003d 1, or x + 3 \u003d - 4, x2 \u003d - 7.

3. Solution of quadratic equations by the formula

Multiply both sides of the equation

ah2+ in+ c = 0, a ≠ 0, on 4a and successively we have:

4a2 x2 + 4abx+ 4ac = 0,

((2ax)2 + 2 axb + b2 ) - b2 + 4ac= 0,

(2ax +b)2 = in2- 4ac,

2ax+ b= ± https://pandia.ru/text/78/082/images/image006_128.gif" width="71" height="27">, x1,2 =

In the case of a positive discriminant, i.e., with v2 - 4ac > 0, equation ah2+ in + s= 0 has two different roots.

If the discriminant is zero, i.e. v2 - 4ac = 0, then the equation ah2+ in+ with= 0 has a single root, x = - https://pandia.ru/text/78/082/images/image009_95.gif" width="14" height="62"> Its roots satisfy the Vieta theorem, which, when a= 1 has the form

x1 x2 = q,

x1 + x2 = - R.

From this we can draw the following conclusions (by the coefficients R and q root signs can be predicted).

a) If a free member q reduced equation (1)
positive (q> 0), then the equation has two identical
by the sign of the root and it depends on the second coefficient R
If a R> 0, then both roots are negative if R< 0, then both
roots are positive.

For example,

x2- 3X + 2 = 0; x1= 2 and x2 = 1, since q = 2 > 0 u p = - 3 < 0;

x2 + 8x + 7 = 0; x 1 \u003d - 7 and x2 \u003d - 1, since q= 7 > 0 and R = 8 > 0.

b) If a free member q reduced equation (1)
negative (q < 0), then the equation has two roots of different sign, and the larger root in absolute value will be positive if R< 0, or negative if p > 0.

For example,

x2 + 4x - 5 = 0; x1 \u003d - 5 and x2 \u003d 1, since q = - 5 < 0 и R= 4 > 0;

x2 - 8x - 9 = 0; x1 = 9 and x2= - 1 because q = - 9 < и R= - 8 < 0.

5. Solution of equations by the method of "transfer"

Consider the quadratic equation ax2 + in+ c = 0, where a ≠ 0. Multiplying both its parts by a, we get the equation a2x2 +abx+ ace= 0.

Let be ah = y where X=; then we come to the equation

y2+ by+ ac = 0,

equivalent to this one. its roots y1 and y2 find with the help of Vieta's theorem. Finally we get x1= https://pandia.ru/text/78/082/images/image012_77.gif" width="24" height="43">.

With this method, the coefficient a is multiplied by the free term, as if “thrown” to it, which is why it is called transfer method. This method is used when it is easy to find the roots of an equation using Vieta's theorem and, most importantly, when the discriminant is an exact square.

1. Solve the equation 2x2 - 11x + 15 = 0.

Decision. Let's "transfer" the coefficient 2 to the free term, as a result we get the equation

y2 - 11 at+ 30 = 0.

According to the Vieta theorem, y1 = 5, y2 = 6, hence x1 = https://pandia.ru/text/78/082/images/image014_69.gif" width="16 height=41" height="41">, t e.

x1 = 2.5 x2 = 3.

Answer: 2,5; 3.

6. Properties of the coefficients of the squareequations

A. Let a quadratic equation be given

ax2 + in + c= 0, where a ≠ 0.

1. If a + in + with= 0 (i.e., the sum of the coefficients of the equation is equal to zero), then x1 = 1, x2 = .

2. If a - b + c= 0, orb = a + c, then x1 = - 1, X 2 = - https://pandia.ru/text/78/082/images/image016_58.gif" width="44 height=41" height="41">.

Answer: 1; 184">

The following cases are possible:

A straight line and a parabola can intersect at two points, the abscissas of the intersection points are the roots of a quadratic equation;

A straight line and a parabola can touch (only one common point), that is, the equation has one solution;

The straight line and the parabola do not have common points, that is, the quadratic equation has no roots.

Examples.

1. Let's graphically solve the equation x2 - 3x - 4 = 0 (Fig. 2).

Decision. We write the equation in the form x2 = 3x + 4.

Let's build a parabola y = x2 and direct y= 3x + 4. Direct at= 3x + 4 can be constructed from two points M(0; 4) and N(3; 13). A line and a parabola intersect at two points A to B with abscissa x1= - 1 and x2 = 4.

Answer: x1= - 1, x, = 4.

8. Solving quadratic equations with a compass and straightedge

We propose the following method for finding the roots of a quadratic equation

ah2+ in+ with= 0

using a compass and ruler (Fig.).

Let us assume that the desired circle intersects the abscissa axis at the points B(x1; 0) and D(x2 ; 0), where x1 and x2- roots of the equation ax2 + in+with=0,
and passes through points A(0; 1) and C(0; ) on the y-axis..gif" width="197" height="123">

So: 1) build points https://pandia.ru/text/78/082/images/image023_40.gif" width="171" height="45"> the circle intersects the OX axis at point B(x1;0), and D(x1 ; 0), where x1 and x2 - roots of the quadratic equation ax2+bx+c = 0.

2) The radius of the circle is equal to the ordinate of the center , the circle touches the x-axis at the point B(x1; 0), where xx is the root of the quadratic equation.

3) The radius of the circle is less than the ordinate of the center left">

https://pandia.ru/text/78/082/images/image029_34.gif" width="612" height="372">40" height="14">

https://pandia.ru/text/78/082/images/image031_28.gif" width="612" height="432 src=">

Whence after substitutions and

simplifications, the equation z2+pz+q=0 follows, and the letter z means the label of any point of the curvilinear scale.

10. Geometric method for solving quadratic equations

And four attached squares i.e. S=x2+10x+25. Replacing x2+10x with 39, we get S = 39 + 25 = 64, which means that the side of the square ABCD, i.e. segment AB= 8. For the desired side X the original square we get

Conclusion

We all know how to solve quadratic equations, from school to graduation. But in the school course of mathematics, the formulas of the roots of quadratic equations are studied, with the help of which any quadratic equations can be solved. However, having studied this issue more deeply, I became convinced that there are other ways to solve quadratic equations that allow you to solve many equations very quickly and rationally.

Maybe mathematics is somewhere out there in other dimensions, not visible to the eye - everything is written down and we just get all the new facts from the hole with the worlds? ... God knows; but it turns out that if physicists, chemists, economists or archaeologists need a new model of the structure of the world, this model can always be taken from the shelf where mathematicians put it three hundred years ago, or assembled from parts lying on the same shelf. Perhaps these parts will have to be twisted, adjusted to each other, polished, quickly machined a couple of new theorem bushings; but the theory of the result will not only describe the actual situation that has arisen, but also predict the consequences! ...

A strange thing is this game of the mind, which is always right ...

Literature

1. Alimov SHA., Ilyin VA. et al. Algebra, 6-8. Trial textbook for 6-8 grades of high school. - M., Education, 1981.

2.Bradis math tables for high school. Ed. 57th. - M., Education, 1990. S. 83.

3. Zlotsky - tasks in teaching mathematics. The book for the teacher. - M., Education, 1992.

4.M., Mathematics (supplement to the newspaper "First of September"), Nos. 21/96, 10/97, 24/97, 18/98, 21/98.

5. Okunev functions, equations and inequalities. A guide for the teacher. - M., Education, 1972.

6. Solomnik B. C., Sweet questions and problems in mathematics. Ed. 4th, add. - M., Higher School, 1973.

7.M., Mathematics (supplement to the newspaper "First of September"), No. 40, 2000.

Review

for the work of a student of the 11th grade of the MOU "Sergievskaya secondary

comprehensive school"

1. METHOD : Factorization of the left side of the equation.

Let's solve the equation

x 2 + 10x - 24 = 0.

Let's factorize the left side:

x 2 + 10x - 24 \u003d x 2 + 12x - 2x - 24 \u003d x (x + 12) - 2 (x + 12) \u003d (x + 12) (x - 2).

Therefore, the equation can be rewritten as:

(x + 12)(x - 2) = 0

2. METHOD : Full square selection method.

Let's solve the equation x 2 + 6x - 7 = 0.

Let's select a full square on the left side.

To do this, we write the expression x 2 + 6x in the following form:

x 2 + 6x = x 2 + 2 x 3.

In the resulting expression, the first term is the square of the number x, and the second is the double product of x by 3. Therefore, to get the full square, you need to add 3 2, since

x 2+ 2 x 3 + 3 2 \u003d (x + 3) 2.

We now transform the left side of the equation

x 2 + 6x - 7 = 0,

adding to it and subtracting 3 2 . We have:

x 2 + 6x - 7 = x 2+ 2 x 3 + 3 2 - 3 2 - 7 = (x + 3) 2 - 9 - 7 = (x + 3) 2 - 16.

Thus, this equation can be written as follows:

(x + 3) 2 - 16 = 0, (x + 3) 2 = 16.

Hence, x + 3 - 4 = 0, x 1 = 1, or x + 3 = -4, x 2 = -7.

3. METHOD :Solution of quadratic equations by formula.

Multiply both sides of the equation

ah 2+bx + c = 0, a ≠ 0

on 4a and successively we have:

4a 2 x 2 + 4abx + 4ac = 0,

((2ax) 2 + 2axb + b 2 ) - b 2 + 4 ac = 0,

(2ax + b) 2 = b 2 - 4ac,

2ax + b \u003d ± √ b 2 - 4ac,

2ax \u003d - b ± √ b 2 - 4ac,

Examples.

a) Let's solve the equation: 4x2 + 7x + 3 = 0.

a = 4,b= 7, c = 3,D = b 2 - 4 ac = 7 2 - 4 4 3 = 49 - 48 = 1,

D > 0, two different roots;

Thus, in the case of a positive discriminant, i.e. at

b 2 - 4 ac >0 , the equation ah 2+bx + c = 0 has two different roots.

b) Let's solve the equation: 4x 2 - 4x + 1 = 0,

a = 4,b= - 4, c = 1,D = b 2 - 4 ac = (-4) 2 - 4 4 1= 16 - 16 = 0,

D = 0, one root;

So, if the discriminant is zero, i.e. b 2 - 4 ac = 0 , then the equation

ah 2+bx + c = 0 has a single root

in) Let's solve the equation: 2x 2 + 3x + 4 = 0,

a = 2,b= 3, c = 4,D = b 2 - 4 ac = 3 2 - 4 2 4 = 9 - 32 = - 13 , D < 0.

This equation has no roots.

So, if the discriminant is negative, i.e. b 2 - 4 ac < 0 ,

the equation ah 2+bx + c = 0 has no roots.

Formula (1) of the roots of the quadratic equation ah 2+bx + c = 0 allows you to find the roots any quadratic equation (if any), including reduced and incomplete. Formula (1) is expressed verbally as follows: the roots of a quadratic equation are equal to a fraction whose numerator is equal to the second coefficient, taken with the opposite sign, plus minus the square root of the square of this coefficient without quadruple the product of the first coefficient by the free term, and the denominator is twice the first coefficient.

4. METHOD: Solution of equations using Vieta's theorem.

As is known, the given quadratic equation has the form

x 2+px + c = 0. (1)

Its roots satisfy the Vieta theorem, which, when a =1 has the form

x 1 x 2 = q,

x 1 + x 2 = - p

From this we can draw the following conclusions (the signs of the roots can be predicted from the coefficients p and q).

a) If the summary term q of the reduced equation (1) is positive ( q > 0 ), then the equation has two roots of the same sign and this is the envy of the second coefficient p. If a R< 0 , then both roots are negative if R< 0 , then both roots are positive.

For example,

x 2 – 3 x + 2 = 0; x 1 = 2 and x 2 = 1, as q = 2 > 0 and p = - 3 < 0;

x 2 + 8 x + 7 = 0; x 1 = - 7 and x 2 = - 1, as q = 7 > 0 and p= 8 > 0.

b) If a free member q of the reduced equation (1) is negative ( q < 0 ), then the equation has two roots of different sign, and the larger root in absolute value will be positive if p < 0 , or negative if p > 0 .

For example,

x 2 + 4 x – 5 = 0; x 1 = - 5 and x 2 = 1, as q= - 5 < 0 and p = 4 > 0;

x 2 – 8 x – 9 = 0; x 1 = 9 and x 2 = - 1, as q = - 9 < 0 and p = - 8 < 0.

5. METHOD: Solving equations using the "transfer" method.

Consider the quadratic equation

ah 2+bx + c = 0, where a ≠ 0.

Multiplying both its parts by a, we obtain the equation

a 2 x 2 + abx + ac = 0.

Let be ah = y, where x = y/a; then we come to the equation

y 2+by+ ac = 0,

equivalent to this one. its roots 1 and at 2 can be found using Vieta's theorem.

Finally we get

x 1 \u003d y 1 / a and x 1 \u003d y 2 / a.

Example.

Let's solve the equation 2x 2 - 11x + 15 = 0.

Decision. Let's "transfer" the coefficient 2 to the free term, as a result we get the equation

y 2 - 11y + 30 = 0.

According to Vieta's theorem

y 1 = 5 x 1 = 5/2x 1 = 2,5

y 2 = 6x 2 = 6/2 x 2 = 3.

Answer: 2.5; 3.

6. METHOD: Properties of the coefficients of a quadratic equation.

BUT. Let the quadratic equation

ah 2+bx + c = 0, where a ≠ 0.

1) If, a+b+ c \u003d 0 (i.e. the sum of the coefficients is zero), then x 1 \u003d 1,

x 2 \u003d s / a.

Proof. We divide both sides of the equation by a ≠ 0, we get the reduced quadratic equation

x 2 + b/ a x + c/ a = 0.

According to Vieta's theorem

x 1 + x 2 = - b/ a,

x 1 x 2 = 1 c/ a.

By condition a -b+ c = 0, where b= a + c. Thus,

x 1 + x 2 = -a+ b / a \u003d -1 - c / a,

x 1 x 2 \u003d - 1 (- c / a),

those. x 1 = -1 and x 2 =c/ a, which we needed to prove.

Examples.

1) Solve the equation 345x 2 - 137x - 208 = 0.

Decision. As a +b+ c \u003d 0 (345 - 137 - 208 \u003d 0), then

x 1 = 1, x 2 =c/ a = -208/345.

Answer: 1; -208/345.

2) Solve the equation 132x 2 - 247x + 115 = 0.

Decision. As a +b+ c \u003d 0 (132 - 247 + 115 \u003d 0), then

x 1 = 1, x 2 =c/ a = 115/132.

Answer: 1; 115/132.

B. If the second coefficient b = 2 k is an even number, then the formula of the roots

Example.

Let's solve the equation 3x2 - 14x + 16 = 0.

Decision. We have: a = 3,b= - 14, c = 16,k = - 7 ;

D = k 2 – ac = (- 7) 2 – 3 16 = 49 – 48 = 1, D > 0, two different roots;