В этой статье собрана начальная информация о системах неравенств. Здесь дано определение системы неравенств и определение решения системы неравенств. А также перечислены основные виды систем, с которыми наиболее часто приходится работать на уроках алгебры в школе, и приведены примеры.
Навигация по странице.
Что такое система неравенств?
Системы неравенств удобно определить аналогично тому, как мы вводили определение системы уравнений , то есть, по виду записи и смыслу, вложенному в нее.
Определение.
Система неравенств – это запись, представляющая собой некоторое число записанных друг под другом неравенств, объединенных слева фигурной скобкой, и обозначающая множество всех решений, являющихся одновременно решениями каждого неравенства системы.
Приведем пример системы неравенств. Возьмем два произвольных , например, 2·x−3>0
и 5−x≥4·x−11
, запишем их одно под другим
2·x−3>0
,
5−x≥4·x−11
и объединим знаком системы – фигурной скобкой, в результате получим систему неравенств такого вида:
Аналогично дается представление о системах неравенств в школьных учебниках. Стоит отметить, что в них определения даются более узко: для неравенств с одной переменной или с двумя переменными .
Основные виды систем неравенств
Понятно, что можно составить бесконечно много различных систем неравенств. Чтобы не заблудиться в этом многообразии, их целесообразно рассматривать по группам, имеющим свои отличительные признаки. Все системы неравенств можно разбить на группы по следующим критериям:
- по числу неравенств в системе;
- по числу переменных, участвующих в записи;
- по виду самих неравенств.
По числу неравенств, входящих в запись, различают системы двух, трех, четырех и т.д. неравенств. В предыдущем пункте мы привели пример системы , которая является системой двух неравенств. Покажем еще пример системы четырех неравенств  .
.
Отдельно скажем, что нет смысла говорить о системе одного неравенства, в этом случае по сути речь идет о самом неравенстве, а не о системе.
Если смотреть на число переменных, то имеют место системы неравенств с одной, двумя, тремя и т.д. переменными (или, как еще говорят, неизвестными). Посмотрите на последнюю систему неравенств, записанную двумя абзацами выше. Это система с тремя переменными x , y и z . Обратите внимание, что ее два первых неравенства содержат не все три переменные, а лишь по одной из них. В контексте этой системы их стоит понимать как неравенства с тремя переменными вида x+0·y+0·z≥−2 и 0·x+y+0·z≤5 соответственно. Заметим, что в школе основное внимание уделяется неравенствам с одной переменной.
Осталось обговорить, какие виды неравенств участвуют в записи систем. В школе в основном рассматривают системы двух неравенств (реже – трех, еще реже - четырех и более) с одной или двумя переменными, причем сами неравенства обычно являются целыми неравенствами
первой или второй степени (реже – более высоких степеней или дробно рациональными). Но не удивляйтесь, если в материалах по подготовке к ОГЭ столкнетесь с системами неравенств, содержащими иррациональные, логарифмические, показательные и другие неравенства. В качестве примера приведем систему неравенств  , она взята из
.
, она взята из
.
Что называется решением системы неравенств?
Введем еще одно определение, связанное с системами неравенств, - определение решения системы неравенств :
Определение.
Решением системы неравенств с одной переменной называется такое значение переменной, обращающее каждое из неравенств системы в верное , другими словами, являющееся решением каждого неравенства системы.
Поясним на примере. Возьмем систему двух неравенств с одной переменной . Возьмем значение переменной x , равное 8 , оно является решением нашей системы неравенств по определению, так как его подстановка в неравенства системы дает два верных числовых неравенства 8>7 и 2−3·8≤0 . Напротив, единица не является решением системы, так как при ее подстановке вместо переменной x первое неравенство обратится в неверное числовое неравенство 1>7 .
Аналогично можно ввести определение решения системы неравенств с двумя, тремя и большим числом переменных:
Определение.
Решением системы неравенств с двумя, тремя и т.д. переменными называется пара, тройка и т.д. значений этих переменных, которая одновременно является решением каждого неравенства системы, то есть, обращает каждое неравенство системы в верное числовое неравенство.
К примеру, пара значений x=1 , y=2 или в другой записи (1, 2) является решением системы неравенств с двумя переменными , так как 1+2<7 и 1−2<0 - верные числовые неравенства. А пара (3,5, 3) не является решением этой системы, так как второе неравенство при этих значениях переменных дает неверное числовое неравенство 3,5−3<0 .
Системы неравенств могут не иметь решений, могут иметь конечное число решений, а могут иметь и бесконечно много решений. Часто говорят о множестве решений системы неравенств. Когда система не имеет решений, то имеет место пустое множество ее решений. Когда решений конечное число, то множество решений содержит конечное число элементов, а когда решений бесконечно много, то и множество решений состоит из бесконечного числа элементов.
В некоторых источниках вводятся определения частного и общего решения системы неравенств, как, например, в учебниках Мордковича . Под частным решением системы неравенств понимают ее одно отдельно взятое решение. В свою очередь общее решение системы неравенств - это все ее частные решения. Однако в этих терминах есть смысл лишь тогда, когда требуется особо подчеркнуть, о каком решении идет речь, но обычно это и так понятно из контекста, поэтому намного чаще говорят просто «решение системы неравенств».
Из введенных в этой статье определений системы неравенств и ее решений следует, что решение системы неравенств представляет собой пересечение множеств решений всех неравенств этой системы.
Список литературы.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2008. - 271 с. : ил. - ISBN 978-5-09-019243-9.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2009. - 271 с. : ил. - ISBN 978-5-09-021134-5.
- Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. - 13-е изд., стер. - М.: Мнемозина, 2011. - 222 с.: ил. ISBN 978-5-346-01752-3.
- Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. - 2-е изд., стер. - М.: Мнемозина, 2008. - 287 с.: ил. ISBN 978-5-346-01027-2.
- ЕГЭ -2013. Математика: типовые экзаменационные варианты: 30 вариантов / под ред. А. Л. Семенова, И. В. Ященко. – М.: Издательство «Национальное образование», 2012. – 192 с. – (ЕГЭ-2013. ФИПИ – школе).
Неравенства и системы неравенств - это одна из тем, которая проходится в средней школе по алгебре. По уровню сложности она является не самой трудной, т. к. имеет незамысловатые правила (о них немного позже). Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано ещё и с тем, что учителя попросту "натаскивают" своих учеников по данной теме. И они не могут этого не делать, ведь она изучается и в дальнейшем с применением иных математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках тема, посвящённая неравенствам и системам неравенств, раскрыта очень подробно, поэтому если вы собираетесь её изучить, то лучше всего прибегнуть именно к ним. Данная статья лишь пересказывает большие материалы, и в ней могут быть некоторые опущения.
Понятие системы неравенств
Если обратиться к научному языку, то можно дать определение понятию "система неравенств". Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: "Решите систему неравенств 4 x + 1 > 2 и 30 - x > 6... "). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.

Системы неравенств и системы уравнений
В процессе изучения новой темы очень часто возникают недопонимания. С одной стороны, всё ясно и скорее хочется приступить к решению заданий, а с другой - какие-то моменты остаются в "тени", не совсем хорошо осмысливаются. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. В результате такого "наложения" зачастую случаются ошибки.

Поэтому перед тем как приступить к разбору нашей темы, следует вспомнить про отличия уравнений и неравенств, их систем. Для этого нужно ещё раз пояснить, что представляют собой данные математические понятия. Уравнение - это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком "="). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Виды неравенств
Выделяют два вида неравенств: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные величины (цифры), неравные друг другу, например, 8 > 10. Второй - это неравенства, содержащие в себе неизвестную переменную (обозначается какой-либо буквой латинского алфавита, чаще всего X). Данная переменная требует своего нахождения. В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).

Два последних вида по степени своего построения и уровню сложности решения делятся на простые и сложные. Простые называют ещё линейными неравенствами. Они, в свою очередь, подразделяются на строгие и нестрогие. Строгие конкретно "говорят", что одна величина обязательно должна быть либо меньше, либо больше, поэтому это в чистом виде неравенство. Можно привести несколько примеров: 8 x + 9 > 2, 100 - 3 x > 5 и т. д. Нестрогие включают в себя ещё и равенство. То есть одна величина может быть больше или равна другой величине (знак "≥") либо меньше или равна другой величине (знак "≤"). Ещё в линейных неравенствах переменная не стоит в корне, квадрате, не делится на что-либо, из-за чего они называются "простыми". Сложные включают в себя неизвестные переменные, нахождение которых требует выполнения большего количества математических операций. Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Свойства неравенств
К свойствам неравенств относятся следующие положения:
- Знак неравенства меняется на обратный, если применяется операция по перемене следования сторон (например, если t 1 ≤ t 2 , то t 2 ≥ t 1).
- Обе части неравенства позволяют прибавить к себе одно и то же число (например, если t 1 ≤ t 2 , то t 1 + число ≤ t 2 + число).
- Два и более неравенств, имеющие знак одного направления, позволяют складывать их левые и правые части (например, если t 1 ≥ t 2 , t 3 ≥ t 4 , то t 1 + t 3 ≥ t 2 + t 4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же положительное число (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
- Два и более неравенств, имеющие положительные члены и знак одного направления, позволяют умножать себя друг на друга (например, если t 1 ≤ t 2 , t 3 ≤ t 4 , t 1 , t 2 , t 3 , t 4 ≥ 0 то t 1 · t 3 ≤ t 2 · t 4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же отрицательное число, но при этом знак неравенства меняется (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
- Все неравенства обладают свойством транзитивности (например, если t 1 ≤ t 2 и t 2 ≤ t 3 , то t 1 ≤ t 3).

Теперь после изучения основных положений теории, относящейся к неравенствам, можно приступить непосредственно к рассмотрению правил решения их систем.
Решение систем неравенств. Общие сведения. Способы решения
Как уже говорилось выше, решением выступают значения переменной, подходящие ко всем неравенствам данной системы. Решение систем неравенств - это осуществление математических действий, которые в итоге приводят к решению всей системы или доказывают, что у неё решений не имеется. В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак "принадлежит") ø (знак "пустое множество"), например, x ∈ ø (читается так: "Переменная "икс" принадлежит пустому множеству"). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
Графический способ
Позволяет решить систему неравенств с несколькими неизвестными величинами (от двух и выше). Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.

Чтобы выполнить решение системы неравенств с помощью графического способа, необходимо все члены каждого неравенства перенести в их левую часть. Знаки поменяются на противоположные, справа следует записать ноль, затем нужно записать каждое неравенство отдельно. В итоге из неравенств получатся функции. После этого можно доставать карандаш и линейку: теперь потребуется нарисовать график каждой полученной функции. Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.
Алгебраический способ
Позволяет решить систему неравенств с двумя неизвестными переменными. Также неравенства должны обладать одинаковым знаком неравенства (т. е. обязаны содержать либо только знак "больше", либо только знак "меньше" и пр.) Несмотря на свою ограниченность, этот способ к тому же и более сложный. Он применяется в двух этапах.
Первый включает себя действия по избавлению от одной из неизвестных переменных. Сначала нужно её выбрать, затем проверить на наличие чисел перед этой переменной. Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким - 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго - на 3. Получится 15y и 15y соответственно.
Второй этап решения. Нужно левую часть каждого неравенства перенести в их правые части с изменением знака каждого члена на противоположный, справа записать нуль. Затем наступает самое интересное: избавление от выбранной переменной (по-другому это называется "сокращение") во время складывания неравенств. Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Способ подстановки
Позволяет решить систему неравенств при наличии возможности ввести новую переменную. Обычно этот способ применяется, когда неизвестная переменная в одном члене неравенства возведена в четвёртую степень, а в другом члене имеет квадрат. Таким образом, данный метод направлен на понижение степени неравенств в системе. Неравенство образца х 4 - х 2 - 1 ≤ 0 данным способом решается так. Вводится новая переменная, например, t. Пишут: "Пусть t = х 2 ", далее модель переписывают в новом виде. В нашем случае получится t 2 - t - 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.
Метод интервалов
Это самый простой способ решения систем неравенств, и в то же время он является универсальным и распространённым. Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
- Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (справа пишется ноль).
- Неравенства выписываются отдельно, определяется решение каждого из них.
- Находятся пересечения неравенств на числовой прямой. Все числа, находящиеся на этих пересечениях, будут являться решением.
Какой способ использовать?
Очевидно тот, который кажется наиболее лёгким и удобным, но бывают такие случаи, когда задания требуют определённого метода. Чаще всего в них написано, что нужно решать либо с помощью графика, либо методом интервалов. Алгебраический способ и подстановка используются крайне редко или не используются вообще, поскольку они достаточно сложные и запутанные, да и к тому же больше применяемы для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов. Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Если что-то не получается
Во время изучения той или иной темы по алгебре, естественно, могут возникнуть проблемы с её пониманием. И это нормально, ведь наш мозг устроен так, что он не способен уяснить сложный материал за один раз. Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: "Решите систему неравенств 3 x + 1 ≥ 0 и 2 x - 1 > 3". Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.

Решебник?
А ещё очень хорошо подойдёт решебник, только не для списывания домашних заданий, а для самопомощи. В них можно найти системы неравенств с решением, посмотреть на них (как на шаблоны), попытаться понять, как именно автор решения справился с поставленной задачей, а затем попытаться выполнить подобное в самостоятельном порядке.
Выводы
Алгебра - это один из самых сложных предметов в школе. Ну что же тут поделать? Математика всегда была такой: кому-то она даётся легко, а кому-то с затруднением. Но в любом случае следует помнить, что общеобразовательная программа построена так, что с ней может справиться любой ученик. К тому же, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.
Неравенство - это два числа или математических выражения, соединённых одним из знаков: > (больше, в случае строгих неравенств), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Неравенство является линейным при тех же условиях, что и уравнение: оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение линейных неравенств и систем линейных неравенств неразрывно связано с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость, на которые всю плоскость делит прямая, уравнением которой задано линейное неравенство. Эту полуплоскость, а в случае системы линейных неравенств - часть плоскости, ограниченную несколькими прямыми, требуется найти на чертеже.
К решению систем линейных неравенств с большим числом переменных сводятся многие экономические задачи, в частности, задачи линейного программирования , в которых требуется найти максимум или минимум функции.
Решение систем линейных неравенств с любым числом неизвестных
Сначала разберём линейные неравенства на плоскости. Рассмотрим одно неравенство с двумя переменными и :
![]() ,
,
где - коэффициенты при переменных (некоторые числа), - свободный член (также некоторое число).
Одно неравенство с двумя неизвестными, так же как и уравнение, имеет бесчисленное множество решений. Решением данного неравенства назовём пару чисел , удовлетворяющих этому неравенству. Геометрически множество решений неравенства изображается в виде полуплоскости, ограниченной прямой
![]() ,
,
которую назовём граничной прямой.
Шаг 1. Построить прямую, ограничивающую множество решений линейного неравенства
Для этого надо знать какие-либо две точки этой прямой. Найдём точки пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1). Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу после этого теретического экскурса.

Абсциссу найдём, решая как систему уравнение прямой с уравнением оси .
Найдём пересечение с осью :

Подставляя значение в первое уравнение, получаем
Откуда .
Таким образом, нашли абсциссу точки A .
Найдём координаты точки пересечения с осью .
Абсцисса точки B равна нулю. Решим уравнение граничной прямой с уравнением оси координат:
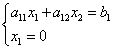
![]() ,
,
следовательно, координаты точки B : .
Шаг 2. Начертить прямую, ограничивающую множество решений неравенства. Зная точки A и B пересечения граничной прямой с осями координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две части, лежащие справа и слева (выше и ниже) от этой прямой.
Шаг 3. Установить, которая из полуплоскостей является решением данного неравенства. Для этого нужно в это неравенство подставить начало координат (0; 0). Если координаты начала удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой находится начало координат. Если же координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, которая не содержит начала координат. Полуплоскость решения неравенства будем обозначать штрихами от прямой внутрь полуплоскости, как на рисунке 1.
Если решаем систему линейных неравенств , то каждый шаг выполняется для каждого из неравенств системы.
Пример 1. Решить неравенство
Решение. Начертим прямую
Подставив в уравнение прямой , получим , а подставив , получим . Следовательно, координаты точек пересечения с осями будут A (3; 0) , B (0; 2) . Через эти точки проведём прямую (опять рисунок 1).

Выберем полуплоскость решений неравенства. Для этого в неравенство подставим координаты начала (0; 0) :
получим , т. е. координаты начала удовлетворяют данному неравенству. Следовательно, решением неравенства является полуплоскость, содержащая в себе начало координат, т. е. левая (она же нижняя) полуплоскость.
Если бы данное неравенство было строгим, то есть имело бы вид
то точки граничной прямой не являлись бы решением, так как они не удовлетворяют неравенству.
Теперь рассмотрим систему линейных неравенств с двумя неизвестными:

Каждое из неравенств этой системы на плоскости определяет полуплоскость. Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Решением системы линейных неравенств называется любая пара чисел (), удовлетворяющая всем неравенствам данной системы.
Геометрически решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам системы, то есть, общая часть получаемых полуплоскостей. Поэтому геометрически в общем случае решение может быть изображено в виде некоторого многоугольника, в частном случае - может быть линия, отрезок и даже точка. Если система линейных неравенств несовместна, то на плоскости не существует ни одной точки, удовлетворяющей всем неравенствам системы.
Пример 2.
Решение. Итак, требуется найти многоугольник решений этой системы неравенств. Построим граничную прямую для первого неравенства, то есть прямую , и граничную прямую для второго неравенства, то есть прямую .
Делаем это пошагово, как было показано в теоретической справке и в примере 1, тем более, что в примере 1 строили граничную прямую для неравенства, которое является первым в данной системе.

Полуплоскости решений, соответствующие неравенствам данной системы, на рисунке 2 заштрихованы вовнутрь. Общая часть полуплоскостей решений представляет собой открытый угол ABC . Это означает, что множество точек плоскости, составляющих открытый угол ABC , является решением как первого, так и второго неравенства системы, то есть, является решением системы двух линейных неравенств. Иначе говоря, кординаты любой точки из этого множества удовлетворяют обоим неравенствам системы.
Пример 3. Решить систему линейных неравенств
Решение. Построим граничные прямые, соответствующие неравенствам системы. Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь определим полуплоскости решений для каждого неравенства (рисунок 3).

Полуплоскости решений, соответствующие неравенствам данной системы, заштрихованы вовнутрь. Пересечение полуплоскостей решений изображается, как показано на рисунке, в виде четырёхугольника ABCE . Получили, что многоугольник решений системы линейных неравенств с двумя переменными является четырёхугольником ABCE .
Всё описанное выше о системах линейных неравенств с двумя неизвестными относится и к системе неравенств с любым числом неизвестных, с той лишь разницей, что решением неравенства с n неизвестными будет совокупность n чисел (), удовлетворяющих всем неравенствам, а вместо граничной прямой будет граничная гиперплоскость n -мерного пространства. Решением будет многогранник решений (симплекс), ограниченный гиперплоскостями.
Свяжем с каждой точкой (x 1 ,x 2 ,…x n) n-мерного пространства R n n-мерный вектор x =(x 1 ,x 2 ,…x n) с началом в начале координат и концом в точке (x 1 ,x 2 ,…x n). Множество векторов х =(х 1 ,х 2 ,...х n) в R n , компоненты которых удовлетворяют m линейным неравенствам:
A 11 х 1 +a 12 х 2 +...+a 1 n x n ≤ b 1
a 21 х 1 +a 22 х 2 +...+a 2 n x n ≤ b 2
. . . . . . . . . . . . (2)
a m 1 х 1 +a m 2 х 2 +...+a m n x n ≤ b m
называется множеством решений системы линейных неравенств.
В определении все неравенства записаны со знаком ≤. Умножая на
(-1) любое из неравенств, можно изменить его знак на противоположный. Множество решений определено для систем линейных неравенств как со знаком ³ так и ≤.
Вопросы моделирования
Предмет теории моделирования
Моделирование - это замещение одного объекта (оригинала) другим (моделью) и фиксация и изучение свойств модели. Замещение производится с целью упрощения, удешевления, ускорения изучения свойств оригинала.
В общем случае объектом-оригиналом может быть естественная или искусственная, реальная или воображаемая система. Она имеет множество параметров и характеризуется определенными свойствами. Количественной мерой свойств системы служит множество характеристик , система проявляет свои свойства под влиянием внешних воздействий .
Множество параметров и их значений отражает ее внутреннее содержание- структуру и принципы функционирования. Характеристики -это в основном ее внешний признаки, которые важны при взаимодействии с другими .
Моделирование целесообразно, когда у модели отсутствуют те признаки оригинала, которые препятствуют его исследованию.
Теория моделирования - взаимосвязанная совокупность положений, определений, методов и средств создания моделей. Сами модели являются предметом теории моделирования.
Теория моделирования является основной составляющей общей теории систем - системологии, где в качестве главного принципа постулируются осуществимые модели: система представима конечным множеством моделей, каждая из которых отражает определенную грань ее сущности.
Роль и место моделирования в исследовании систем.
Познание любой системы () сводится по существу к созданию ее модели. Перед изготовлением каждого устройства или сооружения разрабатывается его модель- проект. Любое произведение искусства является моделью, фиксирующее действительность.
Достижения математики привели к распространению математических моделей различных объектов и процессов. Помечено, что динамика функционирования разных по физической природе систем однотипными зависимостями, что позволяет моделировать их на ПК.
Классификация моделей
Физические модели. В основу классификации положена степень абстрагирования модели от оригинала. Предварительно все модели можно подразделить на 2 группы - физические и абстрактные (математические).
Ф.М. обычно называют систему, эквивалентную или подобную оригиналу, но возможно имеющую другую физическую природу. Виды Ф.М.:
Натуральные;
Квазинатуральные;
Масштабные;
Аналоговые;
Натуральные модели - это реальные исследуемые системы (макеты, опытные образцы). Имеют полную адекватность (соответствия) с системой оригинала, но дороги.
Квазинатуральные модели - совокупность натуральных и математических моделей. Этот вид используется тогда, когда модель части системы не может быть математической из-за сложности ее описания (модель человека оператора) или когда часть системы должна быть исследована во взаимодействии с другими частями, но их еще не существует или их включение очень дорого (вычислительные полигоны, АСУ).
Масштабная модель - это система той же физической природы, что и оригинал, но отличается от него масштабами. Методологической основой масштабного моделирования является теория подобия. При проектировании ВС масштабные модели могут использоваться для анализа вариантов компоновочных решений.
Аналоговыми моделями называются системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей используются механические, гидравлические, пневматические и электрических системы. Аналоговое моделирование используют при исследовании средства ВТ на уровне логических элементов и электрических цепей, а так же на системном уровне, когда функционирование системы описывается например, дифференциальными или алгебраическими уравнениями.
Математические модели. Математические модели представляют собой формализованное представление системы с помощью абстрактного языка, с помощью математических соотношений, отражающих процесс функционирования системы. Для составления математической модели можно использовать любые математические средства - алгебраическое, дифференциальное, интегральное исчисления, теорию множеств, теорию алгоритмов и т.д. По существу вся математика создана для составления и исследования моделей объектов и процессов.
К средствам абстрактного описания систем относятся также языки химических формул, схем, чертежей, карт, диаграмм и т.п. Выбор вида модели определяется особенностями изучаемой системы и целями моделирования, т.к. исследование модели позволяет получить ответы на определенную группу вопросов. Для получения другой информации другой информации может потребоваться модель другого вида. Математические модели можно классифицировать на детерминированные и вероятностные, аналитические, численные и имитационные.
Аналитической моделью называется такое формализованное описание системы, которое позволяет решить уравнение в явном виде, используя известный математический аппарат.
Численная модель характеризуется зависимостью такого вида, который допускает только частные решения для конкретных начальных условий и количественных параметров моделей.
Имитационная модель - это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила не дают возможности использования имеющихся математических методов аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить вычисления интересующих характеристик. Имитационные модели могут быть созданы для гораздо более широкого класса объектов и процессов, чем аналитические и численные. Поскольку для реализации имитационных моделей служат ВС, средствами формализованного описания им служат универсальные и специальные алгоритмические языки. Им в наибольшей степени подходят для исследования ВС на системном уровне.
Рассмотрим ряд задач, в которых необходимо найти область решения системы линейных неравенств.
Пример 1 :
X 1 + 3х 2 ≤ 6
х 1 - х 2 ≤ 2

Искомое множество решений соответствует заштрихованной области. Вершинами множества решений служат три точки (0,2), (0,-2) и (3,1). Ониявляются точками пересечения прямых, ограничивающих множество решений.
В этом примере множество решений - многогранное выпуклое множество.
Пример 2: Изобразить множество решений следующей системы линейных неравенств в R².
X 1 + 2х 2 ≤ 4
3х 1 + 2х 2 ≤ 6

Вершинами искомого множества являются две точки с координатами: (0,2) и (1/2, 9/4). Точка с координатой (0,3) вершиной не является, так как не удовлетворяет первому неравенству. Это множество решений - неограниченно.
РешениеПример 3: Изобразить множество решений следующей системы линейных неравенств в R².
Х 1 - х 2 ³ 1
х 1 + х 2 ≤ 1

Решением первого и второго неравенств являются точки заштрихо-ванного нижнего сектора. Решением третьего неравенства являются точки заштрихованной верхней полуплоскости. Поскольку общих точек у этих двух областей нет, то нет решения и у всей системы неравенств, т.е решением является Æ.
Основная задача линейного программирования.
В общем виде задача линейного программирования (ЗЛП) ставится следующим образом.
Найти вектор х =(х 1 ,х 2 , ... x n) в R n , который максимизирует (или минимизирует) целевую функцию
F(x)=с 1 х 1 +с 2 x 2 +... +с n x n (3)
и удовлетворяет m+n линейным неравенствам:
A 11 х 1 +a 12 x 2 +...+a 1n x n ≤ b 1
a 21 x 1 +a 22 x 2 +...+a 2n x n ≤ b 2
. . . . . . . . . . . . (4)
a m1 x 1 +a m2 x 2 +...+a mn x n ≤ b m
x 1 ³0, x 2 ³0, ... x n ³0
В терминологии программирования линейная функция F(х) называется целевой функцией задачи. Множество решений системы линейных неравенств (4) называют множеством допустимых решений, а любой вектор х из этого множества называется допустимым решением. Оптимальным решением называется вектор х *, при котором целевая функция принимает своё максимальное (или минимальное) значение на допустимом множестве решений.
Графический метод решения задач линейного программирования. Покажем, как решается указанная задача графическим (геометрическим) методом. Для этого ограничимся рассмотрением системы линейных неравенств с двумя неизвестными.
Пусть задана целевая функция F=с 1 х 1 +с 2 х 2 +с 0 . Найдём среди множества точек (х 1 ,х 2) из области допустимых решений совместной системы неравенств (4) (содержащей только переменные x 1 и x 2) такие, которые придают линейной функции F наименьшее (наибольшее) значения. Для каждой i – ой точки плоскости функция F принимает фиксированное значение F=F i . Множество всех таких точек на которых функция F принимает одно и то же значение F i есть прямая с 1 х 1 +c 2 х 2 +c 0 =F i = const, перпендикулярная к некоторому вектору, называемому градиентом F (grad F). Этот вектор выходит из начала координат и имеет координаты grad F =(с 1 ,с 2). По свойству вектора grad F если указанную прямую передвигать параллельно самой себе в положительном направлении вектора grad F, то значение целевой функции F=с 1 х 1 +с 2 х 2 +с 0 на этой прямой будет возрастать, а в противоположном направлении - убывать.
Пусть при движении прямой F=const в положительном направлении вектора grad F эта прямая впервые встретится с многоугольником допустимых решений в его вершине. Тогда в этом положении F 1 прямая F=const называется опорной, и на этой прямой функция F принимает наименьшее значение. При дальнейшем движении в том же направлении (положительном) прямая F=const пройдёт через другую вершину многоугольника допустимых решений и выходя из области решений также станет опорной прямой F 2 . На ней функция F принимает наибольшее значение среди всех значений, принимаемых на многоугольнике допустимых решений. Таким образом, минимизация и максимизация целевой функции F=с 1 х 1 +с 2 х 2 +с 0 на многоугольнике допустимых решений достигается в точках пересечения этого многоугольника с опорными прямыми F=с 1 х 1 +с 2 х 2 +с 0 = const, нормальными к вектору grad F=(с 1 , с 2). Это пересечение опорной прямой с множеством допустимых решений может быть либо в одной точке (вершине многоугольника), либо в бесконечном множестве точек (если это множество сторона многоугольника).
Задание по первой, второй, третьей задаче выбирается по фамилии имени отчеству студента, а по четвертой задаче выбирается по фамилии и отчеству.
Задача №1
Таблица 1
| Первая буква | Фамилия | Имя | Отчество | ||||||||||||
| a 11 | a 12 | a 21 | a 2 2 | a 31 | a 32 | a 41 | a 4 2 | b 1 | b 2 | b 3 | C0 | C1 | C2 | ||
| А | |||||||||||||||
| Б | |||||||||||||||
| В | |||||||||||||||
| Г | |||||||||||||||
| Д | |||||||||||||||
| Е | |||||||||||||||
| Ж | |||||||||||||||
| З | |||||||||||||||
| И | |||||||||||||||
| К | |||||||||||||||
| Л | |||||||||||||||
| М | |||||||||||||||
| Н | |||||||||||||||
| О | |||||||||||||||
| П | |||||||||||||||
| Р | |||||||||||||||
| С | |||||||||||||||
| Т | |||||||||||||||
| У | |||||||||||||||
| Ф | |||||||||||||||
| Х | |||||||||||||||
| Ц | |||||||||||||||
| Ч | |||||||||||||||
| ШЭ | |||||||||||||||
| ЮЯ | |||||||||||||||
Пример 4: Минимизировать линейную форму F=14x 1 +4x 2 при ограничениях:
7х 1 + 2х 2 ³ 14
4 х 1 –7x 2 ≤ 14
Заменив знаки неравенств на знаки точных равенств, получим уравнения границ области допустимых решений. По уравнениям, полученных прямых построим искомую область:
7х 1 +2х 2 =14
4 х 1 – 7x 2 = 14
Областью допустимых решений системы неравенств является многоугольник ABCDE.
 рис 5.
рис 5.
Для нахождения точек экстремума построим прямую F=14x 1 +4x 2 =0 и вектор gradF = (14, 4). Будем передвигать прямую F=0 параллельно самой себе в направлении вектора grad F. С многоугольником ABCDE эта прямая впервые встретиться в точках Е(2,0) и А(10/9, 28/9), где целевая функция принимает одно и то же минимальное значение F(E) = F(A) =14·2+4∙0=28-min, (т.к. вектор grad F перпендикулярен прямой АЕ). Таким образом, минимальное значение целевая функция принимает в любой точке отрезка AE.
Из плана ![]() основной задачи линейного программирования следует, что число его положительных компонент не превышает .
основной задачи линейного программирования следует, что число его положительных компонент не превышает .
Опорный план называется невырожденным, если он содержит ровно положительных компонент; в противном случае план является вырожденным.
Любые переменных системы линейных уравнений с переменными (при условии ) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные переменных называются не основными.
Базисным решением системы m линейных уравнений с переменными называется всякое ее решение, в котором все не основные переменные имеют нулевые значения.
Теорема 1 . Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.
Теорема 2 . Если задача линейного программирования имеет оптимальное решение, то оно совпадает с угловой точкой множества допустимых решений.
Следствие. Если оптимальное решение не единственное, то таких решений будет множество (например, все точки отрезка, соединяющего соответствующие угловые точки).
Теорема 3 . Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых значений, и наоборот.
Понятие о симплекс-методе .
Решение основной задачи линейного программирования геометрическим методом достигает большой наглядности в случае 2-х и 3-х переменных. Для случая же большего числа переменных геометрический метод становится невозможным. Так называемый симплекс-метод принадлежит к числу аналитических методов решения основной задачи линейного программирования. При этом ограничения, используемые при реализации симплекс-метода, обычно задаются системой линейных уравнений
A 11 х 1 +a 12 х 2 +...+a 1n x n = b 1
a 21 х 1 +a 22 х 2 +...+a 2n x n = b 2
. . . . . . . . . . . . (5)
a m 1 х 1 +a m 2 х 2 +...+a mn x n = b m
среди неотрицательных решений которой ищутся такие, которые максими-зировали бы линейную (целевую) функцию
F=с 1 х 1 +с 2 х 2 +…+с n х n +с 0
Симплексный метод основан на теоремах:
Теорема 1. Если ЗЛП имеет оптимальное решение, то целевая функция принимает экстремальное значение в одной из угловых точек выпуклого многоугольника допустимых решений.
Теорема 2. Каждому опорному решению ЗЛП соответствует угловая точка многоугольника допустимых решений и наоборот.
Исходя из этих теорем, при реализации симплекс-метода осуществляется целенаправленный перебор всех вершин так, чтобы в каждой следующей вершине значение целевой функции было бы не меньше (не больше) чем в предыдущей вершине. При этом за конечное число шагов достигается искомое оптимальное решение, или устанавливается, что ЗЛП неразрешима.
Для осуществления указанного алгоритма выберем в системе (5) max набор линейно независимых переменных (тех, для которых определитель составленный из коэффициентов перед этими переменными отличен от 0). Пусть для определенности это будут переменные х 1 , х 2 ,... х r (r ≤ m). Выразим эти переменные через остальные переменные
Х 1 = а" 1, r +1 х г+1 + ... + a" 1 n х n + b 1 "
х 2 = а" 2, r +1 х г+1 + ... + a" 2 n х n + b 2 " (6)
. . . . . . . . . . . . . . . .
х r = a" r , r +1 х г+1 + ... + a" r n x n + b r "
причем будем предполагать, что все b 1 "³0, b 2 "³0, b r "³0. Если исходные ограничительные условия заданы неравенствами, то их можно преобразовать к виду (5) путём введения новых неотрицательных переменных, так называемых балансовых (выравнивающих). Так, например,в неравенствеа 1 х 1 +а 2 х 2 +…+а n х n ≤ b достаточно добавить к левой части неравенства некоторую величину х n +1 ³ 0 равную разности между правой и левой частями неравенства и мы получим равенство a 1 x 1 + а 2 х 2 +…+а n х n + x n +1 = b. Если ограничительные условия заданы смешанным образом, то есть неравенствами и уравнениями, тогда указанным путём их так же можно свести только к уравнениям.
В полученной системе (6) переменные (неизвестные) х 1 ,х 2 ... х г называются базисными, а весь набор {х 1 , х 2 ... х г } - базисом, остальные переменные называются свободными. Система ограничений (6) называется системой, приведённой к единичному базису. Подставляя в целевую функцию F вместо базисных переменных их выражения через свободные из системы (6) получим
F = C 0 + C г+1 х г+1 + … + C n х n
Теперь, полагая все свободные переменные равными нулю, найдём значения базисных переменных:
х 1 =b 1 " , х 2 = b 2 " , ... x r =b r "
Полученное таким образом допустимое решение системы (6)
(b 1 " ,b 2 " , ... b r " , 0, ... 0) называется базисным. Для этого базисного решения значение целевой функции будет равно F Б = C 0.
Решение задачи при помощи симплекс-метода распадается на ряд шагов, заключающихся в том, что от данного базиса Б мы переходим к другому базису Б" с таким расчётом, чтобы значение F Б на новом базисе увеличивалось или, по крайней мере, не уменьшалось, то есть выполнялось F Б " ≥ F Б. При этом если все b 1 ">0, b 2 ">0,…., b r ">0 , то данное решение называется опорным и соответствует какой-нибудь угловой точке области допустимых решений определяемой исходной системой ограничений. Тогда переход от одного базисного (опорного) решения к другому соответствует переходу от одной вершины многоугольника допустимых решений к другой вершине.
ЗАДАЧА№2
Для реализации трех групп товаров коммерческое предприятие располагает тремя видами органических материально-денежных ресурсов в количестве , , единиц. При этом для продажи 1 группы товаров на 1 тыс.руб. товарооборота расход утерся в количестве единиц, ресурса второго вида в количестве единиц, ресурса третьего вида в количестве единиц. Для продажи 2 и 3 групп товара на 1 тыс.руб. товарооборота расходуется соответственно ресурса первого вида в количестве , единиц, ресурсов второго вида в количестве , единиц, ресурсов третьего вида в количестве , единиц. Прибыль от одах трех групп товаров на 1тыс.руб. товарооборота составляет соответственно , , (тыс.руб.).
Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.
| Первая буква | Фамилия | Имя | Отчество | ||||||||||||
| А | |||||||||||||||
| Б | |||||||||||||||
| В | 1 0 | ||||||||||||||
| Г | |||||||||||||||
| Д | |||||||||||||||
| Е | |||||||||||||||
| Ж | |||||||||||||||
| З | |||||||||||||||
| И | |||||||||||||||
| К | |||||||||||||||
| Л | |||||||||||||||
| М | |||||||||||||||
| Н | |||||||||||||||
| О | |||||||||||||||
| П | |||||||||||||||
| Р | |||||||||||||||
| С | |||||||||||||||
| Т | |||||||||||||||
| У | |||||||||||||||
| Ф | |||||||||||||||
| Х | |||||||||||||||
| Ц | |||||||||||||||
| Ч | |||||||||||||||
| Ш Э | |||||||||||||||
| Ю Я |
Пример 5: Максимизировать целевую функцию F=-х 4 +х 5 при ограничениях:

Данная система уравнений совместна, так как ранги матрицы системы
 и расширенной матрицы
и расширенной матрицы 
совпадают и равны 3. Выражая базисные переменные (стоящие в единичных столбцах) х 1 , х 2 , х 3 , через свободные переменные х 4 и х 5 , приходим к системе
 (7)
(7)
Помимо системы (7) базисные переменные выразим через свободные переменные и в целевой функции (в нашем примере F = -x 4 + x 5 уже выражена через свободные переменные x 4 и x 5). Полагая теперь х 4 = 0, х 5 =0 находим базисные переменные: х 1 =1, х 2 =2, х 3 =3. Таким образом, первое допустимое базисное решение системы уравнений есть (1, 2, 3, 0, 0) . При найденном допустимом решении целевая функция F имеет значение 0, то есть F 1 =0.
Теперь попытаемся увеличить значение F 1 . Увеличение х 4 уменьшит F 1 , так как перед х 4 в выражении F = -x 4 + x 5 стоит отрицательный коэффициент, а увеличение x 5 даёт увеличение F 1 . Увеличим поэтому x 5 так, чтобы х 1 , х 2 , х 3 , не стали отрицательными, оставив х 4 =0. Из второго уравнения (7) видим, что х 5 можно увеличить до 2 (так, чтобы x 2 оставалось бы 0, при x 4 = 0). Тогда значение переменных будут (5, 0, 1, 0, 2), а значение F 2 = 2. Как видно величина F на втором шаге увеличилась.
Поскольку x 2 и x 4 оказались равными 0, то далее примем за свободные неизвестные х 2 и х 4 , тогда х 5 = 2-х 2 +2х 4
и от системы (7) переходим к эквивалентной ей системе (8)
 (8)
(8)
Причем и F в этом случае будет равной
F = 2-х 2 +х 4
Для увеличения F будем увеличивать х 4 (так как перед x 2 стоитотрицательный коэффициент) Из второго уравнения системы (8) видно, что при условии неотрицательного х 3 значение х 4 можно довести до х 4 =1/5, тогда имеем (28/5, 0, 0, 1/5, 12/5), F 3 =11/5.
Поскольку в решении получено x 2 = x 3 = 0, то примем x 2 и x 3 за свободные переменные и выразим х 1 , х 4 , х 5 , через х 2 и х 3 .Получим
X 1 = 28/5 - 7/5 x 2 - 3/5 x 3
x 4 = 1/5 + 1/5 x 2 – 1/5 x 3
x 5 = 12/5 – 3/5 x 2 – 2/5 x 3
причем F = 11/5 – 4/5 x 2 – 1/5 x 3
Так как коэффициенты при x 2 и при x 3 в выражении для F отрицательны, то увеличить значение F уже невозможно. Поэтому полагая х 2 = х 3 =0 получаем наибольшее значение F = 11/5 при решении (28/5, 0, 0, 1/5, 12/5)
Ответ: F max = 11/5 при X * = (28/5, 0, 0, 1/5, 12/5)
Симплексные таблицы.
Поскольку решать ЗЛП, используя такие рассуждения, как это делалось в предыдущем примере, явно неудобно для компактной записи решения, а так же для возможности программирования алгоритма решения на ЭВМ используются так называемые симплекс-таблицы. Для этого систему ограничений сведем к единичному базису
х 1 + а 1, r +1 х г+1 + ... + a 1 n х n = b 1
х i + а i,r+1 х г+1 + .... + a i n х n = b i (9)
х r + а r,r+1 х г+1 + ... + a r n х n = b r
а целевую функцию F - к виду:
F = C г+1 x r +1 + ... + C j х j +…+ C n x n + C 0 (10)
Равенство (10) будем называть приведённым (к свободным переменным) выражением для функции F а коэффициенты C j – оценками (индексами) соответствующих свободных переменных х j .
Коэффициенты приведенной выше системы ограничений (9), а так же различные вспомогательные переменные заносятся в симплексную таблицу (Таблица 1)
Таблица 1
| Базисные перемен-ные | Свободные члены | х 1 | ... | х i | ... | x r | х г+1 | ... | x j | ... | х n | |
| х 1 | b 1 | ... | ... | а 1,r+1 | ... | a 1j | ... | a 1n | ||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ||
| х i | b i | ... | ... | а i,r+1 | ... | a ij | ... | a in | ||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| x r | b r | ... | ... | а r,r+1 | ... | a rj | ... | a rn | ||||
| F= | C 0 | ... | ... | - C г+1 | ... | - C j | ... | - C n |
Первые r столбцов с неизвестными x i - это единичные столбцы при базисных переменных x 1 ,…,x r . Следующие n-r столбцов – это столбцы при свободных переменных x r +1 ,…,x n . Полагая свободные переменные x r +1 = …=
X n = 0, находим базисные переменные x 1 = b 1 ,…, x r = b r . При этом значение целевой функции F = C 0 .
Найденный вектор-план X 1 = и значение целевой функции F = C 0 соответствуют некоторой вершине многоугольника допустимых решений. Переход к другой вершине и, следовательно, к другому вектор-плану и другому значению целевой функции осуществляется с помощью пересчета данной симплексной таблицы.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
