Площадь криволинейной трапеции
Криволинейной трапецией называется фигура, ограниченная графиком заданной на сегменте [a , b ] непрерывной и неотрицательной фукнции f (x ), ординатами, проведенными в точках a и b , и отрезком оси Ox между точками a и b (см. Рис. 2).
Докажем следующее утверждение.
Криволинейная трапеция представляет собой квадрируемую фигуру, площадь P
Доказательство . Так как непрерывная на сегменте [a , b ] функция интегрируема, то для любого положительного числа ε можно указать такое разбиение T сегмента [a , b ], что разность S - s < ε , где S и s - соответственно верхняя и нижняя суммы разбиения T . Но S и s равны соответственно S d и S i , где S d и S i - площади ступенчатых фигур (многоугольников), первая из которых содержит криволинейную трапецию, а вторая содержится в криволинейной трапеции (на Рис. 2 изображены также и указанные ступенчатые фигуры). Так как S d - S i < ε , то, в силу теоремы 1, криволинейная трапеция квадрируема. Поскольку предел при Δ → 0 верхних и нижних сумм равен и s ≤ P ≤ S , то площадь P криволинейной трапеции может быть найдена по формуле (1).
Замечание . Если функция f (x ) непрерывна и неположительна на сегменте [a , b ], то значение интеграла равно взятой с отрицательным знаком площади криволинейной трапеции, ограниченной графиком функции f (x ), ординатами в точках a и b и отрезком оси Ox между точками a и b . Поэтому, еслиf (x ) меняет знак, то равен сумме взятых с определенным знаком площадей криволинейных трапеций, расположенных выше и ниже оси Ox , причем площади первых берутся со знаком +, а вторых со знаком -.
Площадь криволинейного сектора
Пусть кривая L задана в полярной системе координат уравнением r = r (θ ), α ≤ θ ≤ β (см. Рис. 3), причем функция r (θ ) непрерывна и неотрицательна на сегменте [α , β ]. Плоскую фигуру, ограниченную кривой L и двумя лучами, составляющими с полярной осью углы α и β , будем называть криволинейным сектором .
Докажем следующее утверждение. Криволинейный сектор представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле
Доказательство . Рассмотрим разбиение T сегмента [α , β ] точками α = θ 0 < θ 1 < ... < θ n = β и для каждого частичного сегмента [θ i -1 , θ i ] построим круговые секторы, радиусы которых равны минимальному r i и максимальному R i значениям r (θ ) на сегменте [θ i -1 , θ i ]. В результате получим две веерообразные фигуры, первая из которых содержится в криволинейном секторе, а вторая содержит криволинейный сектор (эти веерообразные фигуры изображены на Рис. 3). Площади и указанных веерообразных фигур равны соответственно и . Отметим, что первая из этих сумм является нижней суммойs для функции для указанного разбиения T сегмента [α , β ], а вторая сумма является верхней суммой S для этой же функции и этого же разбиения. Так как функция интегрируема на сегменте [α , β ], то разность может быть как угодно малой. Например, для любого фиксированного ε > 0 эта разность может быть сделана меньше ε /2. Впишем теперь во внутреннюю веерообразную фигуру многоугольник Q i с площадью S i , для которого , и опишем вокруг внешней веерообразной фигуры многоугольник Q d площадью S d , для которого * . Очевидно, первый из этих многоугольников вписан в криволинейный сектор, а второй описан вокруг него. Так как справедливы неравенства
№____ Дата________
Тема: Криволинейная трапеция и ее площад ь
Цели урока : Дать определения криволинейной трапеции и ее площади, научиться вычислять площадь криволинейной трапеции.
ХОД УРОКА
1. Организационный момент.
Приветствие учащихся, проверка готовности класса к уроку, организация внимания учащихся, раскрытие общих целей урока и плана его проведения.
2. Этап проверки домашнего задания.
Задачи: Установить правильность, полноту и осознанность выполнения д/з всеми учащимися, выявить пробелы в знаниях и способах деятельности учащихся. Определить причины возникновения затруднений, устранить обнаруженные пробелы.
3.Этап актуализации.
Задачи: обеспечение мотивации учения школьников, включение в совместную деятельность по определению целей урока. Актуализировать субъективный опыт учащихся.
Вспомним основные понятия и формулы.
Определение. Функция y= f (x), x (a,b), называется первообразной для функции y=f(x), x (a,b), если для каждого x (a,b) выполняется равенство
F (x)=f(x) .
Замечание. Если f (x) есть первообразная для функции f(x) , то при любой константе С , F(x)+C также является первообразной для f(x).
Задача нахождения всех первообразных функции f(x) называется интегрированием, а множество всех первообразных называется неопределенным интегралом для функции f(x) по dx и обозначается
Имеют место свойства:
1 . ;
2
. Если С=
Const, то 
;
3
. 
.
Замечание. В школьном курсе математики не употребляется термин «неопределенный интеграл», вместо этого говорят «множество всех первообразных».
Приведем таблицу неопределенных интегралов.
Пример 1.
Найти первообразную для функции 
, проходящую через точку М
(2;4).
Решение.
Множество всех первообразных функции есть неопределенный интеграл 
. Вычислим его, используя свойства интеграла 1
и 2
. Имеем:
Получили, что множество всех первообразных задается семейством функций y=F(x)+C , то есть y=x 3 – 2x+C , где С – произвольная постоянная.
Зная, что первообразная проходит через точку М (2;4), подставим ее координаты в предыдущее выражение и найдем С .
4=2 3 –2 2+С С =4–8+4; С =0.
Ответ: F(x)=x 3 - 2x – искомая первообразная.
4. Формирование новых понятий и способов действия.
Задачи: Обеспечить восприятие, осмысление и запоминание учащимися изучаемого материала. Обеспечить усвоение учащимися методики воспроизведения изученного материала, содействовать философскому осмыслению усваиваемых понятий, законов, правил, формул. Установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления, провести коррекцию. Обеспечить соотнесение учащимися своего субъективного опыта с признаками научного знания.
Нахождение площадей плоских фигур
Задача нахождения площади плоской фигуры тесно связана с задачей нахождения первообразных (интегрированием). А именно: площадь криволинейной трапеции ограниченной графиком функции y=f(x) (f(x)> 0) прямыми x=a; x=b; y= 0, равна разности значений первообразной для функции y=f(x) в точках b и a :
S=F(b)–F(a)
Дадим определение определенного интеграла.
О
пределение.
Пусть функция y=f(x)
определена и интегрируема на отрезке [a,b
] и пусть F(x)
– некоторая ее первообразная. Тогда число F(b)–F(a)
называется интегралом от а
до b
функции f(x)
и обозначается
.
Равенство 
называется формулой Ньютона–Лейбница.
Эта формула связывает задачу нахождения площади плоской фигуры с интегралом.
В общем случае, если фигура ограничена графиками функций y=f(x) ; y=g(x) (f(x)>g(x) ) и прямыми x=a ; x=b , то ее площадь равна:
.
Пример2. В какой точке графика функции y=x 2 + 1 надо провести касательную, чтобы она отсекала от фигуры, образованной графиком этой функции и прямыми y= 0, x= 0, x= 1 трапецию наибольшей площади?
Решение. Пусть M 0 (x 0 ,y 0 ) – точка графика функции y=x 2 + 1, в которой проведена искомая касательная.
Найдем уравнение касательной y=y 0 +f (x 0 )(x–x 0 ) .
Имеем: 
Поэтому 
.
Найдем площадь трапеции ОАВС .
.
B – точка пересечения касательной с прямой x= 1
Задача свелась к нахождению наибольшего значения функции
S (x )=–x 2 +x+ 1 на отрезке . Найдем S (x )=– 2x+ 1. Найдем критическую точку из условия S (x )= 0 x= .
Видим, что функция достигает наибольшего значения при x=
. Найдем 
.
Ответ:
касательную надо провести в точке 
.
Отметим, что часто встречается задача нахождения интеграла, исходя из его геометрического смысла. Покажем на примере, как решается такая задача.
Пример 4. Используя геометрический смысл интеграла вычислить
а
) 
; б) 
.
Решение.
а) – равен площади криволинейной трапеции, ограниченной линиями .
П
реобразуем
– верхняя половина окружности с центром Р
(1;0) и радиусом R=
1.
Поэтому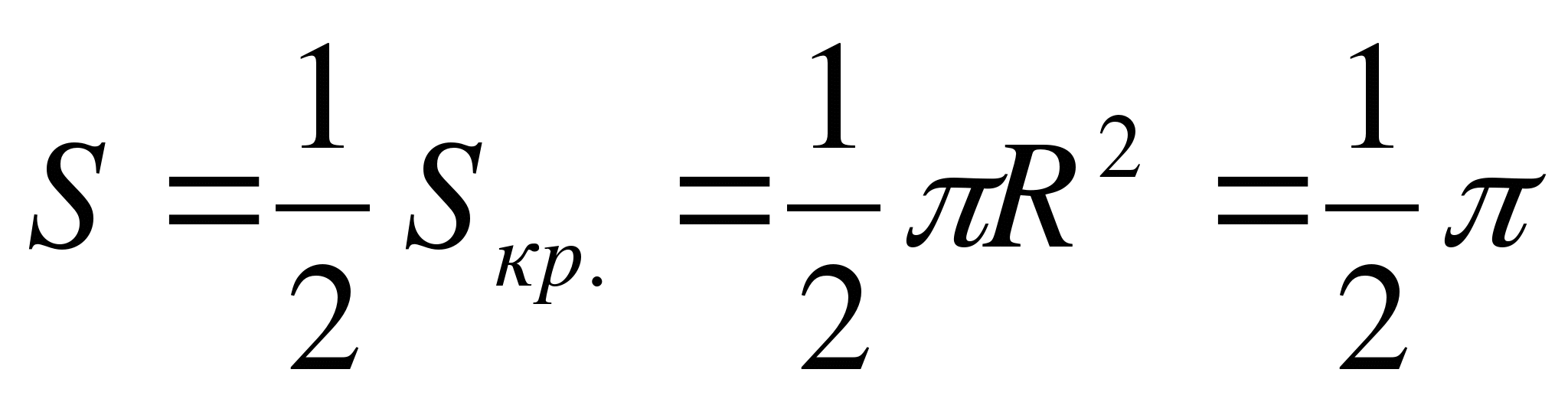 
.
Ответ:
.
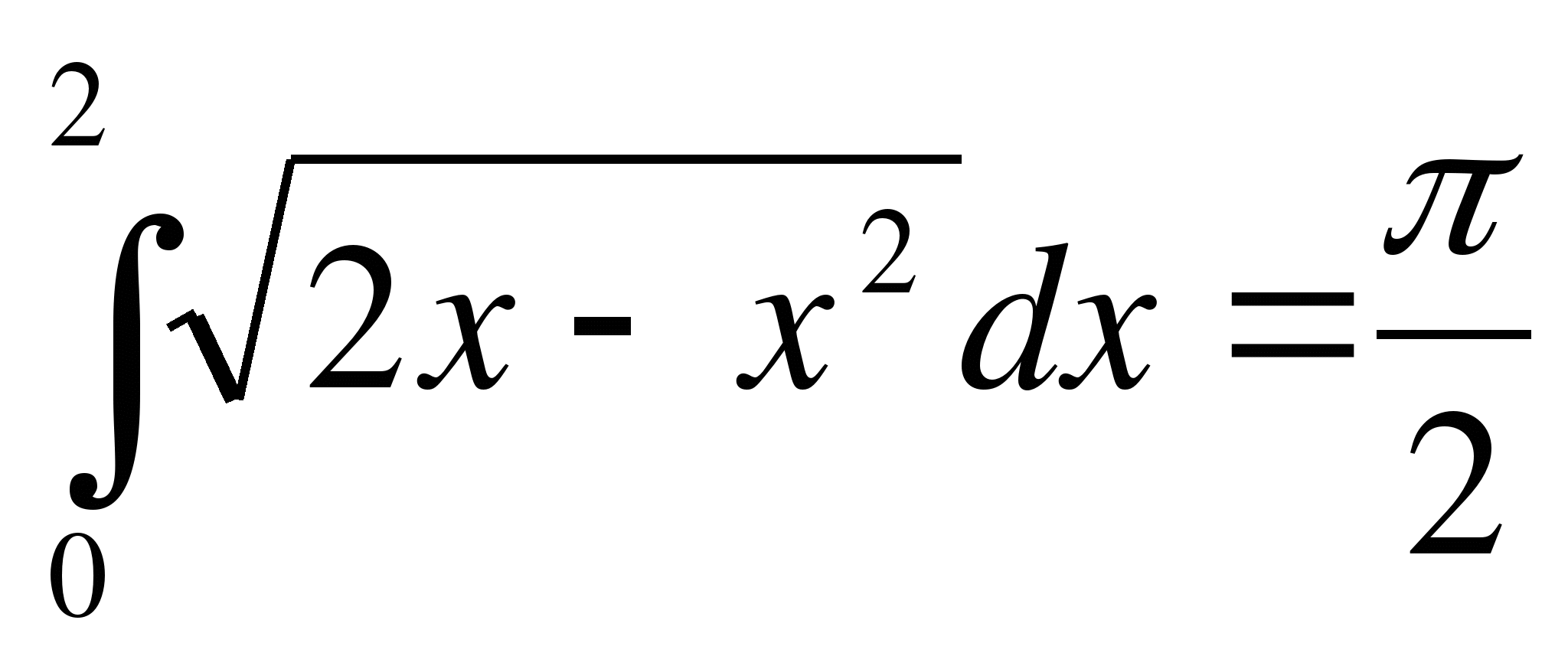б) Рассуждая аналогично, построим область, ограниченную графиками .2
–
2x+
2, касательными к ней в точках A
, B
(4;2)
y= –9x– 59, параболой y= 3x 2 +ax+ 1, если известно, что касательная к параболе в точке x=– 2 составляет с осью Ox угол величиной arctg 6.
Найти а , если известно, что площадь криволинейной трапеции, ограниченной линиями y= 3x 3 + 2x, x=a, y= 0, равна единице.
Найти наименьшее значение площади фигуры, ограниченной параболой y=x 2 + 2x– 3 и прямой y=kx+ 1.
6.Этап информации о домашнем задании.
Задачи: Обеспечить понимание учащимися цели, содержания и способов выполнения домашнего задания.№18, 19,20,21 нечетные
7.Подведение итогов урока.
Задача: Дать качественную оценку работы класса и отдельных учащихся.
У этого термина существуют и другие значения, см. Трапеция (значения). Трапеция (от др. греч. τραπέζιον «столик»; … Википедия
I Площадь одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П.… …
Методы получения численных решений различных задач путём графических построений. Г. в. (графическое умножение, графическое решение уравнений, графическое интегрирование и т. д.) представляют систему построений, повторяющих или заменяющих… … Большая советская энциклопедия
Площадь, одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П. было уже в древности… … Большая советская энциклопедия
Теорема Грина устанавливает связь между криволинейным интегралом по замкнутому контуру C и двойным интегралом по области D, ограниченной этим контуром. Фактически, эта теорема является частным случаем более общей теоремы Стокса. Теорема названа в … Википедия
Определение. Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абцисс и прямыми x=a, x=b, называется криволинейной трапецией.
Способы нахождения площади криволинейной трапеции
Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке , то площадь соответствующей криволинейной трапеции равна приращению первообразных.
Дано: f(x)- непрерывная неопр. функция, xО.
Доказать: S = F(b) - F(a), где F(x) - первообразная f(x).
Доказательство:
1) Рассмотрим вспомогательную функцию S(x). Каждому xО поставим в соответствие ту часть криволинейной трапеции, которая лежит левее прямой (рис. 2), проходящей через точку с этой абциссой и параллельно оси ординат.
Следовательно S(a)=0 и S(b)=Sтр
Докажем, что S(a) - первообразная f(x).
D(f) = D(S) =
S"(x0)= lim(S(x0+Dx) - S(x0) / Dx), при Dx®0 DS - прямоугольник
Dx®0 со сторонами Dx и f(x0)
S"(x0) = lim(Dx f(x0) /Dx) = lim f(x0)=f(x0): т.к. x0 точка, то S(x) -
Dx®0 Dx®0 первообразная f(x).
Следовательно по теореме об общем виде первообразной S(x)=F(x)+C.
Т.к. S(a)=0, то S(a) = F(a)+C
S = S(b)=F(b)+C = F(b)-F(a)
1). Разобьем отрезок на n равных частей. Шаг разбиения (рис. 3)
Dx=(b-a)/n. При этом Sтр=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx=n®Ґ = lim Dx(f(x0)+f(x1)+...+f(xn))
При n®Ґ получим, что Sтр= Dx(f(x0)+f(x1)+...+f(xn))
Предел этой суммы называют определенным интегралом.
Сумма стоящая под пределом, называется интегральной суммой.
Определенный интеграл это предел интегральной суммы на отрезке при n®Ґ. Интегральная сумма получается как предел суммы произведений длины отрезка, полученного при разбиении области определения функции в какой либо точке этого интервала.
a - нижний предел интегрирования;
b - верхний.
Формула Ньютона-Лейбница.
Сравнивая формулы площади криволинейной трапеции делаем вывод:
если F - первообразная для b на , то
т f(x)dx = F(b)-F(a)
т f(x)dx = F(x) ф = F(b) - F(a)
Свойства определенного интеграла.
т f(x)dx = т f(z)dz
т f(x)dx = F(a) - F(a) = 0
т f(x)dx = - т f(x)dx
т f(x)dx = F(a) - F(b) т f(x)dx = F(b) - F(a) = - (F(a) - F(b))
Если a, b и c любые точки промежутка I, на котором непрерывная функция f(x) имеет первообразную, то
т f(x)dx = т f(x)dx + т f(x)dx
F(b) - F(a) = F(c) - F(a) + F(b) - F(c) = F(b) - F(a)
(это свойство аддитивности определенного интеграла)
Если l и m постоянные величины, то
т (lf(x) +m j(x))dx = l т f(x)dx + m тj(x))dx -
Это свойство линейности определенного интеграла.
т (f(x)+g(x)+...+h(x))dx = т f(x)dx+ т g(x)dx+...+ т h(x)dx
т (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) - (F(a) + G(a) +...+ H(a)) +C = F(b)-F(a)+C1 +G(b)-G(a)+C2+...+H(b)-H(a)+Cn=b b b = т f(x)dx+ т g(x)dx+...+ т h(x)dx
Набор стандартных картинок (рис. 4, 5, 6, 7, 8)
Рис. 4
Рис. 6 Рис. 7
Т.к. f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)і0.
Надо: рассмотреть симметрию функции относительно оси OX. ABCD®A"B"CD b
S(ABCD)=S(A"B"CD) = т -f(x)dx
S= т f(x)dx = т g(x)dx
S = т (f(x)-g(x))dx+т(g(x)-f(x))dx
S= т (f(x)+m-g(x)-m)dx =
т (f(x)- g(x))dx
т ((f(x)-g(x))dx
S= т (f(x)+m-g(x)-m)dx =
Т (f(x)- g(x))dx
Если на отрезке f(x)іg(x), то площадь между этими графиками равна
т ((f(x)-g(x))dx
Функции f(x) и g(x) произвольные и неотрицательные
S=т f(x)dx - т g(x)dx = т (f(x)-g(x))dx
Определение. Разность F (b)– F (a) называется интегралом от функции f (x) на отрезке [ a ; b ] и обозначается так: = F (b)– F (a) – формула Ньютона-Лейбница.
Геометрический смысл интеграла.
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b:
Вычисление площадей с помощью интеграла.
1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b:
2.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и прямыми х=а, х= b:
3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и :
4.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и осью Ох:
Задачи и тесты по теме "Интеграл. Вычисление площадей с помощью интеграла"
- Интеграл
Уроков: 4 Заданий: 13 Тестов: 1
- Вычисление площадей с помощью интегралов - Первообразная и интеграл 11 класс
Уроков: 1 Заданий: 10 Тестов: 1
- Первообразная - Первообразная и интеграл 11 класс
Уроков: 1 Заданий: 11 Тестов: 1
- Планиметрия: вычисление длин и площадей
Заданий: 7
- Вычисления и преобразования - Подготовка к ЕГЭ по математике ЕГЭ по математике
Заданий: 10
Прежде чем начать вычислять площадь фигуры, ограниченной заданными линиями, постарайтесь изобразить эту фигуру в системе координат. Это существенно облегчит решение задачи.
Изучение теоретических материалов по данной теме дает Вам возможность овладеть понятиями первообразной и интеграла, усвоить связь между ними, овладеть простейшей техникой интегрального исчисления, научится применять интеграл к вычислению площадей фигур, ограниченных графиками функций.
Примеры.
1. Вычислить интеграл
Решение:
Ответ: 0.
2. Найти площадь фигуры, ограниченной линиями
a) f ( x ) = 2 х – х 2 и осью абсцисс
Решение: График функции f(x) = 2x - х 2 парабола. Вершина: (1; 1).
Ответ: (кв. ед.).