Bir geometrik ilerleme örneğinin ilk n sayısının toplamı. Sonsuz bir geometrik ilerlemenin toplamı. Geometrik ilerlemeye neden ihtiyaç duyulur ve tarihi?

Anna Malkova

Geometrik ilerleme ikinciden başlayarak her bir terimi bir önceki terim ile sabit bir q sayısının çarpımına eşit olan bir dizidir:

Sabit numara Q geometrik ilerlemenin paydası denir.

Geometrik ilerlemenin n'inci terimi için formül:

İlkinin toplamı için formül Geometrik ilerlemenin üyeleri aşağıdaki formülle hesaplanır:

İkinciden başlayarak geometrik ilerlemenin her teriminin karesi, komşularının çarpımına eşittir:

1. Gölün yüzeyinde yosun yetişir. Bir gün içinde her alg ikiye bölünür ve bir alg yerine iki alg ortaya çıkar. Bir gün sonra ortaya çıkan alglerin her biri ikiye bölünür ve bu böyle devam eder. 30 gün sonra göl tamamen yosunlarla kaplandı. Gölün yarıya dolması ne kadar sürdü?

Cevap paradoksaldır: 29 gün sonra.

Bu sorun en iyi şekilde “sondan” çözülür. Burada önünüzde yosunlarla dolu bir göl var. Bir gün önce ne oldu? Açıkçası, yarısı kadar yosun vardı, yani göl yarı onlarla kaplıydı.

Gölde her gün iki kat daha fazla yosun vardı, yani sayıları arttı geometrik ilerlemede.

2. Birleşik Devlet Sınavı) İşadamı Bublikov, 2000 yılında 5.000 ruble kar elde etti. Sonraki her yıl, karı bir önceki yıla göre %300 arttı. Bublikov 2003'te kaç ruble kazandı?

Bublikov'un 2000 yılındaki karı küçüktü. Ancak her yıl kâr bir önceki yıla göre %300 yani 4 kat arttı. Geometrik ilerleme! Dördüncü üyesini arıyoruz:

3. (Birleşik Devlet Sınavı görevi) Alpha Company, gelecek vaat eden sektöre 2001 yılında 3.000 $ sermayeyle yatırım yapmaya başladı. 2002 yılından bu yana her yıl bir önceki yılın sermayesinin %100'ü oranında kâr elde etmektedir. Beta Şirketi ise 2003 yılında 6.000 $ sermaye ile başka bir sektöre yatırım yapmaya başladı ve 2004'ten bu yana bir önceki yılın sermayesinin %200'ü kadar yıllık kar elde etti. Karlar dolaşımdan çekilmeseydi, 2006 yılı sonunda bir şirketin sermayesi diğerinin sermayesinden kaç dolar daha fazlaydı?

Problemin temel kavramlarını tanımlayalım.

Şirket sermayesi– Şirketin kullanabileceği tüm fonların toplamı.

Kâr– gelir ve giderler (maliyetler) arasındaki fark.

Eğer 2002 yılında Alpha şirketinin karı bir önceki yılın sermayesinin %100'ü ise bu, Alpha şirketinin sermayesinin yıl içinde iki katına çıktığı anlamına gelir. Aynı şekilde Alpha'nın sermayesi de 2003, 2004, 2005 ve 2006'da ikiye katlandı, yani 2006'da binlerce dolar oldu.

Beta şirketinin sermayesi yılda 3 kez artıyor. 2006 yılında 2003 yılına göre birkaç kat artarak dolara ulaştı.

Bu, Alpha şirketinin sermayesinden 66 bin dolar daha fazla.

Sonsuz azalan geometrik ilerleme

Paydası |q| olan geometrik bir ilerleme<1, называется бесконечно убывающей.

Sonsuz azalan geometrik ilerlemeye bir örnek.

Miktarı nedir?

Alanı 1 olan bir dikdörtgen çizelim. Alanı olan alanları buna ekleyin

Ortaya çıkan şeklin alanı n'deki sonsuz artışla, yani giderek daha küçük alanların eklenmesiyle ne eğilimi gösterir? Açıkçası, ikiye kadar.

Sonsuz azalan geometrik ilerlemenin toplamı, aşağıdaki formülle bulunan bir sayıdır:

Matematiksel bir şaka var, şimdi anlayacaksınız.

Sonsuz sayıda matematikçi bir bara girer. İlki şöyle diyor: "Bir bardak bira içeceğim!" İkincisi: "Yarım bardak bira alacağım!" Üçüncüsü: "Çeyrek bardak bira içeceğim!" Dördüncüsü: "Bir bardak bira içeceğim!" Barmen: "Durun bir dakika... Numaralarınızı biliyorum; herkese iki bardak biranız var!"

Bağımsız çözüm için Birleşik Devlet Sınavı sorunları

1. İşadamı Korovin, 2000 yılında 1.400.000 ruble kar elde etti. Sonraki her yıl karı bir önceki yıla göre %20 arttı. Korovin 2004'te kaç ruble kazandı?

2. Alpha Company, 2001 yılında gelecek vaat eden bir sektöre 4.000 $ sermayeyle yatırım yapmaya başladı. 2002 yılından bu yana her yıl bir önceki yılın sermayesinin %100'ü oranında kâr elde etmektedir. Beta Şirketi ise 2004 yılında 4.500 $ sermaye ile başka bir sektöre yatırım yapmaya başladı ve 2005'ten bu yana bir önceki yılın sermayesinin %200'ü kadar yıllık kar elde etti. Karlar dolaşımdan çekilmeseydi, 2007 yılı sonunda bir şirketin sermayesi diğerinin sermayesinden kaç dolar daha fazlaydı?

1. Cevap: 2 903 040
2. Cevap: 134500

SAYISAL DİZİLER VI

§ l48. Sonsuz azalan geometrik ilerlemenin toplamı

Şimdiye kadar toplamlardan bahsederken, bu toplamlardaki terim sayısının sonlu olduğunu (örneğin 2, 15, 1000 vb.) varsayıyorduk. Ancak bazı problemleri (özellikle yüksek matematik) çözerken sonsuz sayıda terimin toplamlarıyla uğraşmak gerekir.

S= A 1 + A 2 + ... + A N + ... . (1)

Bu miktarlar nedir? A-tarikatı sonsuz sayıda terimin toplamı A 1 , A 2 , ..., A N , ... S toplamının limiti olarak adlandırılır N Birinci P sayılar ne zaman P -> ∞ :

S=S N = (A 1 + A 2 + ... + A N ). (2)

Limit (2) elbette mevcut olabilir veya olmayabilir. Buna göre (1) toplamının var ya da yok olduğunu söylüyorlar.

Her özel durumda toplam (1)'in mevcut olup olmadığını nasıl öğrenebiliriz? Ortak karar Bu konu programımızın kapsamını çok aşıyor. Ancak önemli bir şey var özel durumşimdi bunu dikkate almamız gerekiyor. Sonsuz azalan bir geometrik ilerlemenin terimlerinin toplanmasından bahsedeceğiz.

İzin vermek A 1 , A 1 Q , A 1 Q 2, ... sonsuz azalan bir geometrik ilerlemedir. Bu şu anlama gelir: | Q |< 1. Сумма первых P bu ilerlemenin şartları eşittir

Değişkenlerin limitlerine ilişkin temel teoremlerden (bkz. § 136) şunu elde ederiz:

Fakat 1 = 1, a qn = 0. Bu nedenle

Yani sonsuz azalan bir geometrik ilerlemenin toplamı, bu ilerlemenin ilk teriminin bir eksi bu ilerlemenin paydasına bölünmesine eşittir.

1) 1, 1/3, 1/9, 1/27, ... geometrik ilerlemesinin toplamı şuna eşittir:

ve geometrik ilerlemenin toplamı 12'dir; -6; 3; - 3/2 , ... eşit

2) Basit bir periyodik kesir olan 0,454545'i sıradan bir kesire dönüştürün.

Bu sorunu çözmek için bu kesri sonsuz bir toplam olarak hayal edin:

Bu eşitliğin sağ tarafı, ilk terimi 45/100, paydası 1/100 olan sonsuz azalan geometrik ilerlemenin toplamıdır. Bu yüzden

Açıklanan yöntemi kullanarak aynı zamanda elde edilebilir. Genel kural basit periyodik kesirlerin sıradan kesirlere dönüştürülmesi (bkz. Bölüm II, § 38):

Basit bir periyodik kesiri sıradan bir kesire dönüştürmek için aşağıdakileri yapmanız gerekir: payda ondalık kesrin periyodunu ve paydaya - dönemdeki basamak sayısı kadar alınan dokuzdan oluşan bir sayı ondalık kesir.

3) Karışık periyodik kesir 0,58333 ....'yi sıradan bir kesire dönüştürün.

Bu kesri sonsuz bir toplam olarak düşünelim:

Bu eşitliğin sağ tarafında 3/1000'den başlayarak tüm terimler, ilk terimi 3/1000, paydası 1/10 olan sonsuz azalan geometrik dizi oluşturur. Bu yüzden

Açıklanan yöntemi kullanarak, karışık periyodik kesirleri sıradan kesirlere dönüştürmek için genel bir kural elde edilebilir (bkz. Bölüm II, § 38). Burada bilinçli olarak sunmuyoruz. Bu hantal kuralı hatırlamanıza gerek yok. Herhangi bir karışık periyodik kesirin, sonsuz azalan geometrik ilerlemenin ve belirli bir sayının toplamı olarak temsil edilebileceğini bilmek çok daha faydalıdır. Ve formül

Sonsuza kadar azalan geometrik ilerlemenin toplamı için elbette şunu hatırlamanız gerekir.

Bir alıştırma olarak, aşağıda verilen 995-1000 numaralı problemlere ek olarak, bir kez daha 301 § 38 numaralı probleme dönmenizi öneriyoruz.

Egzersizler

995. Sonsuza kadar azalan geometrik ilerlemenin toplamına ne denir?

996. Sonsuz azalan geometrik ilerlemelerin toplamlarını bulun:

997. Hangi değerlerde X ilerleme

sonsuz mu azalıyor? Böyle bir ilerlemenin toplamını bulun.

998. Kenarları olan bir eşkenar üçgende A kenarlarının orta noktaları birleştirilerek yeni bir üçgen yazılır; bu üçgenin içine aynı şekilde yeni bir üçgen yazılır ve bu böyle sonsuza kadar devam eder.

a) tüm bu üçgenlerin çevrelerinin toplamı;

b) alanlarının toplamı.

999. Kenarlı kare A kenarlarının orta noktaları birleştirilerek yeni bir kare yazılır; Bu karenin içine de aynı şekilde bir kare yazılır ve bu böyle sonsuza kadar devam eder. Bu karelerin çevrelerinin toplamını ve alanlarının toplamını bulun.

1000. Toplamı 25/4 ve terimlerinin kareleri toplamı 625/24 olacak şekilde sonsuz azalan bir geometrik dizi oluşturun.

Geometrik ilerleme, ilk terimi sıfırdan farklı olan ve sonraki her terimin bir önceki terimin aynı değerle çarpımına eşit olduğu sayısal bir dizidir. sıfıra eşit sayı.

Geometrik ilerleme gösterilir b1,b2,b3, …, bn, … .

Geometrik hatanın herhangi bir teriminin bir önceki terimine oranı aynı sayıya eşittir, yani b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( n+1)/bn = … . Bu doğrudan tanımdan kaynaklanmaktadır aritmetik ilerleme. Bu sayıya geometrik ilerlemenin paydası denir. Genellikle geometrik ilerlemenin paydası q harfiyle gösterilir.

Monoton ve sabit dizi

Geometrik ilerlemeyi belirtmenin bir yolu, onun ilk terimini b1 ve geometrik hata q'nun paydasını belirtmektir. Örneğin b1=4, q=-2. Bu iki koşul 4, -8, 16, -32,… geometrik ilerlemesini tanımlar.

Eğer q>0 ise (q, 1'e eşit değildir), o zaman ilerleme şu şekildedir: monoton dizi.Örneğin 2, 4,8,16,32, ... dizisi monoton olarak artan bir dizidir (b1=2, q=2).

Geometrik hatanın paydası q=1 ise geometrik ilerlemenin tüm terimleri birbirine eşit olacaktır. Bu gibi durumlarda ilerlemenin olduğunu söylüyorlar sabit sıra.

Geometrik ilerlemenin n'inci terimi için formül

Bir sayı dizisinin (bn) geometrik dizi olabilmesi için ikinciden başlayarak her bir üyesinin komşu üyelerin geometrik ortalaması olması gerekir. Yani aşağıdaki denklemin yerine getirilmesi gerekir
(b(n+1))^2 = bn * b(n+2), herhangi bir n>0 için; burada n, N doğal sayılar kümesine aittir.

Geometrik ilerlemenin n'inci teriminin formülü:

bn=b1*q^(n-1),

burada n, N doğal sayılar kümesine aittir.

Geometrik ilerlemenin ilk n teriminin toplamı için formül

Geometrik ilerlemenin ilk n teriminin toplamına ilişkin formül şu şekildedir:

Sn = (bn*q - b1)/(q-1), burada q, 1'e eşit değildir.

Basit bir örneğe bakalım:

Geometrik ilerlemede b1=6, q=3, n=8 Sn'yi bulun.

S8'i bulmak için geometrik ilerlemenin ilk n teriminin toplamı formülünü kullanırız.

S8= (6*(3^8 -1))/(3-1) = 19.680.

Konuyla ilgili ders “Sonsuzca azalan geometrik ilerleme”

Dersin amacı:Öğrencileri yeni bir dizi türüyle tanıştırıyoruz - sonsuz azalan geometrik ilerleme.

Görevler:

sayısal bir dizinin limitine ilişkin başlangıç ​​fikrinin formüle edilmesi; sonsuz azalan geometrik ilerlemenin toplamı formülünü kullanarak sonsuz periyodik kesirleri sıradan kesirlere dönüştürmenin başka bir yolunu bilmek;

okul çocuklarının kişiliğinin entelektüel niteliklerinin geliştirilmesi mantıksal düşünme, değerlendirici eylemler yeteneği, genelleme;

faaliyeti, karşılıklı yardımlaşmayı, kolektivizmi ve konuya ilgiyi teşvik etmek.

Teçhizat: bilgisayar sınıfı, projektör, ekran.

Ders türü: ders - öğrenme yeni Konu.

Dersler sırasında

BEN . Organizasyon an. Dersin konusunu ve amacını belirtin.

II . Öğrencilerin bilgilerinin güncellenmesi.1. Ödevleri kontrol etmek.

1) Aritmetik ve geometrik ilerlemelerle ilgili temel formüllerin kontrol edilmesi. İki öğrenci tahtada formüllerle ilgili notlar hazırlıyor.

2) Öğrencilerin geri kalanı bunu yapar “Toplam Formülleri” konusunda matematiksel dikte.

Görevler:

№1. Bir aritmetik ilerlemenin ilk terimi 6 (1. seçenek), -20 (2. seçenek) ve beşinci terimi -6 (1. seçenek), 20 (2. seçenek) ise, ilk beş teriminin toplamını bulun.

№2. Bir aritmetik ilerlemenin ilk terimi -20 (1. seçenek), 6 (2. seçenek) ve fark 10 (1. seçenek), -3 (2. seçenek) ise, ilk beş teriminin toplamını bulun.

№3. İlk terimi 1 (1. seçenek), -1 (2. seçenek) ve paydası -2 (1. seçenek), 2 (2. seçenek) ise, geometrik ilerlemenin ilk beş teriminin toplamını bulun.

Diktenin sonunda, seçici olarak iki öğrencinin çalışması değerlendirme için kontrol edilir, geri kalanı kendi kendine test yapar. hazır çözümler, tahtanın kanatlarına yazılmıştır.

Çözümler:

Görevler

1. Aritmetik ilerleme formülle verilir A N = 7 – 4 N. Bulmak A 10 . (-33)

2. Aritmetik ilerlemede A 3 = 7 Ve A 5 = 1 . Bulmak A 4 . (4)

3. Aritmetik ilerlemede A 3 = 7 Ve A 5 = 1 . Bulmak A 17 . (-35)

4. Aritmetik ilerlemede A 3 = 7 Ve A 5 = 1 . Bulmak S 17 . (-187)

5. Geometrik ilerleme için
beşinci terimi bulunuz.

6. Geometrik ilerleme için
bulmak Nüye.

7. Üstel olarak B 3 = 8 Ve B 5 = 2 . Bulmak B 4 . (4)

8. Üstel olarak B 3 = 8 Ve B 5 = 2 . Bulmak B 1 Ve Q .

9. Üstel olarak B 3 = 8 Ve B 5 = 2 . Bulmak S 5 . (62)

III . Yeni bir konu öğrenmek(sunumun gösterimi).

Bir kenarı 1'e eşit olan bir kare düşünün. Kenarı ilk karenin yarısı kadar olan başka bir kare, sonra kenarı ikinci karenin yarısı kadar olan başka bir kare, sonra bir sonrakini vb. çizelim. Her seferinde yeni karenin kenarı bir öncekinin yarısına eşittir.

Sonuç olarak, bir dizi kare kenar elde ettik paydayla geometrik bir ilerleme oluşturuyoruz.

Ve çok önemli olan, bu tür kareleri ne kadar çok inşa edersek, karenin kenarı da o kadar küçük olacaktır. Örneğin,

Onlar. N sayısı arttıkça ilerlemenin terimleri sıfıra yaklaşır.

Bu şekli kullanarak başka bir diziyi düşünebilirsiniz.

Örneğin karelerin alanlarının sırası:

. Ve yine eğer N süresiz olarak artarsa ​​alan sıfıra istediğiniz kadar yaklaşır.

Başka bir örneğe bakalım. Kenarları 1 cm'ye eşit olan eşkenar üçgen. Aşağıdaki teoreme göre, köşeleri 1. üçgenin kenarlarının orta noktalarında olan bir sonraki üçgeni oluşturalım. orta çizgiüçgen - 2.'nin kenarı birincinin kenarının yarısına eşittir, 3.'nün kenarı 2.'nin kenarının yarısına eşittir, vb. Yine üçgenlerin kenarlarının uzunluklarının bir dizisini elde ediyoruz.

en
.

Negatif paydalı bir geometrik ilerlemeyi düşünürsek.

Daha sonra sayıları giderek artan Nİlerleme açısından sıfıra yaklaşıyor.

Bu dizilerin paydalarına dikkat edelim. Her yerde paydaların mutlak değeri 1'den küçüktü.

Şu sonuca varabiliriz: eğer paydasının modülü 1'den küçükse geometrik ilerleme sonsuza kadar azalacaktır.

Ön çalışma.

Tanım:

Paydanın modülü birden küçükse geometrik ilerlemenin sonsuz azalan olduğu söylenir.
.

Tanımı kullanarak geometrik ilerlemenin sonsuz azalıp azalmadığına karar verebilirsiniz.

Görev

Aşağıdaki formülle verilirse dizi sonsuz azalan bir geometrik ilerleme midir?

;
.

Çözüm:

. Bulacağız Q .

;
;
;
.

bu geometrik ilerleme sonsuz biçimde azalmaktadır.

B) bu dizi sonsuz derecede azalan bir geometrik ilerleme değildir.

Bir kenarı 1'e eşit olan bir kare düşünün. Onu ikiye bölün, yarımlardan birini ikiye bölün, vb. Ortaya çıkan tüm dikdörtgenlerin alanları sonsuz derecede azalan bir geometrik ilerleme oluşturur:

Bu şekilde elde edilen tüm dikdörtgenlerin alanlarının toplamı 1. karenin alanına eşit ve 1'e eşit olacaktır.

Ancak bu eşitliğin sol tarafında sonsuz sayıda terimin toplamı bulunmaktadır.

İlk n terimin toplamını ele alalım.

Geometrik ilerlemenin ilk n teriminin toplamına ilişkin formüle göre, şuna eşittir: .

Eğer N sınırsız artarsa

veya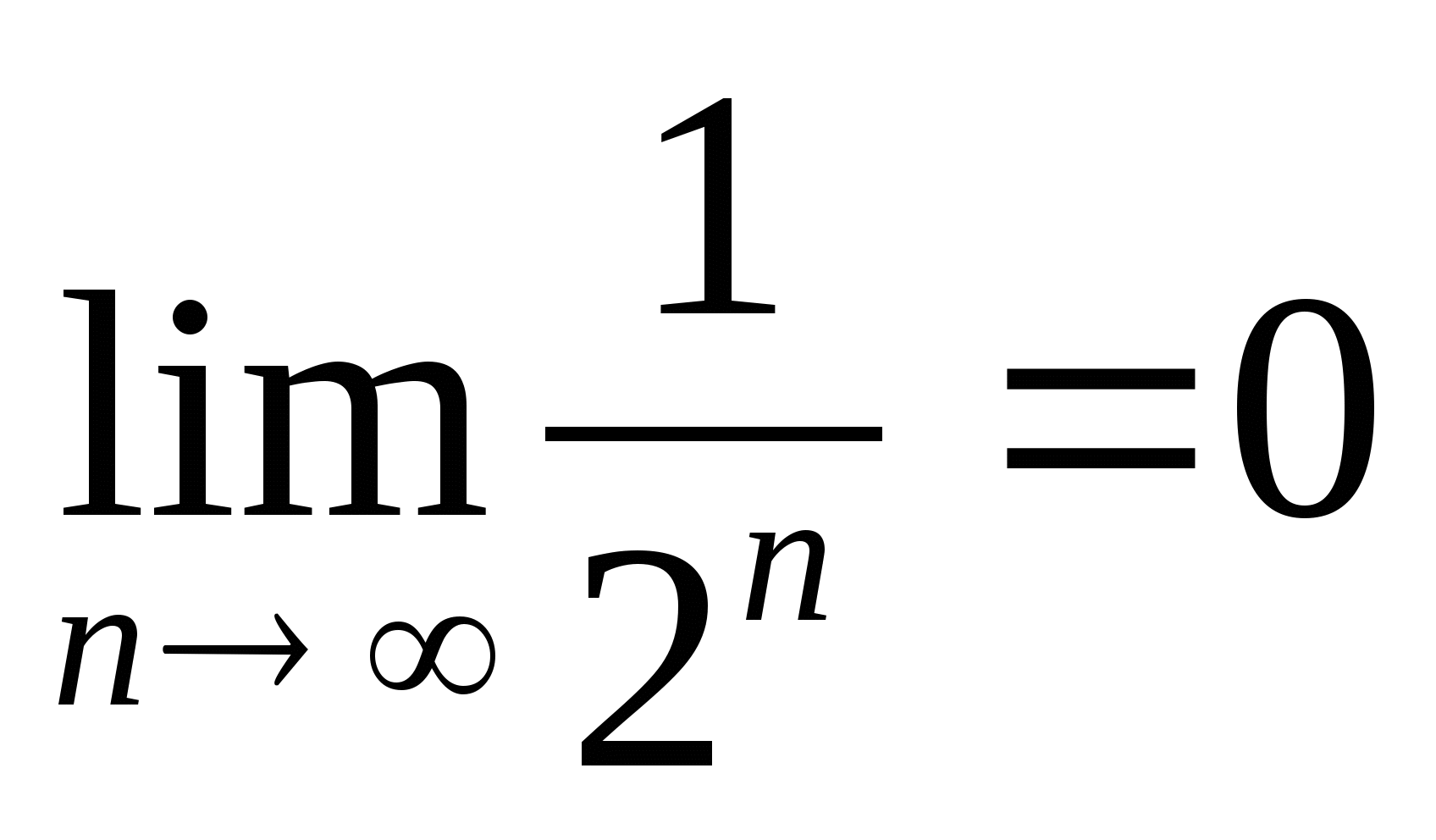
. Bu yüzden
, yani
.

Sonsuz azalan geometrik ilerlemenin toplamı bir dizi sınırı var S 1 , S 2 , S 3 , …, S N , … .

Örneğin, ilerleme için
,

Çünkü

Sonsuz azalan geometrik ilerlemenin toplamı formül kullanılarak bulunabilir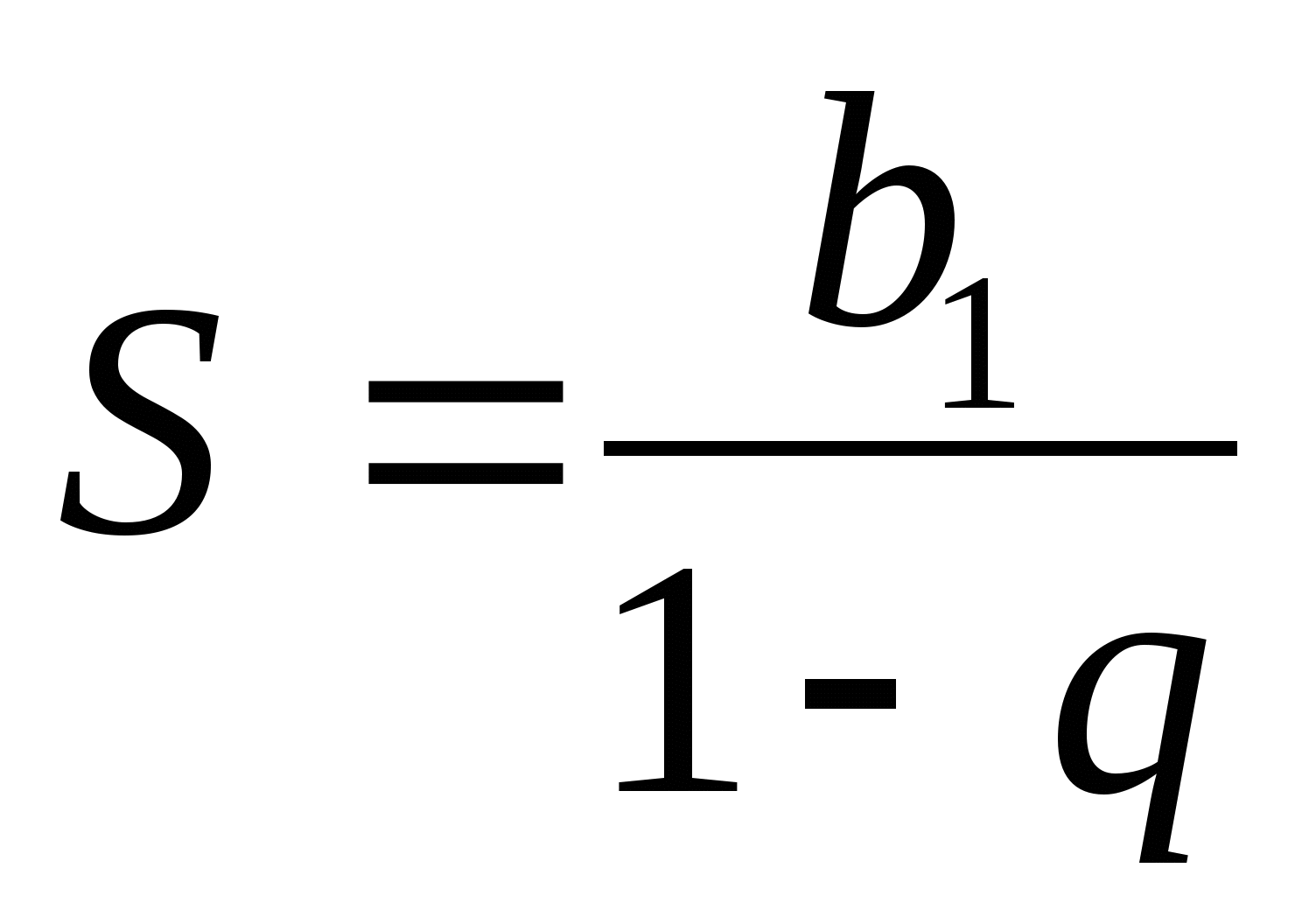
.

III . Anlama ve birleştirme(görevleri tamamlamak).

Görev No.2. İlk terimi 3 ve ikinci terimi 0,3 olan sonsuz azalan geometrik ilerlemenin toplamını bulun.

Çözüm:

Görev No.3. ders kitabı, s. 160, Sayı 433(1)

Sonsuz azalan geometrik ilerlemenin toplamını bulun:

Çözüm:

Görev No.4. Sonsuz periyodik ondalık kesir 0,(5)'i ortak kesir olarak yazın.

1. yöntem. x=0,(5)= 0,555… / 10 2. yöntem olsun. 0,(5)=0,555…=

Görev No.5. ders kitabı, s. 162, No. 445(3) (bağımsız çözüm)

Sonsuz periyodik ondalık kesir 0,(12)'yi ortak kesir olarak yazın.

Cevap: 0,(12)= 4/33.

IV . Özetleme.

Bugün hangi diziyle tanıştınız?

Sonsuz azalan geometrik ilerlemeyi tanımlayın.

Geometrik ilerlemenin sonsuza kadar azaldığı nasıl kanıtlanır?

Sonsuz azalan geometrik ilerlemenin toplamının formülünü verin.

V . Ev ödevi.

Örneğin, dizi \(3\); \(6\); \(12\); \(24\); \(48\)... geometrik bir ilerlemedir, çünkü sonraki her öğe öncekinden iki kat farklıdır (başka bir deyişle, öncekinden ikiyle çarpılarak elde edilebilir):

Herhangi bir dizi gibi, geometrik ilerleme de küçük bir Latin harfiyle gösterilir. Bir dizi oluşturan sayılara denir üyeler(veya öğeler). Geometrik ilerlemeyle aynı harfle gösterilirler, ancak sırayla öğenin numarasına eşit bir sayısal indeksle gösterilirler.

Örneğin, geometrik ilerleme \(b_n = \(3; 6; 12; 24; 48…\)\) \(b_1=3\); elemanlarından oluşur \(b_2=6\); \(b_3=12\) vb. Başka bir deyişle:

Yukarıdaki bilgileri anlarsanız, bu konudaki sorunların çoğunu zaten çözebileceksiniz.

Örnek (OGE):
Çözüm:

Cevap : \(-686\).

Örnek (OGE): Progresyonun ilk üç terimi \(324\) verilmiştir; \(-108\); \(36\)…. \(b_5\) bulun.
Çözüm:

	Diziye devam etmek için paydayı bilmemiz gerekiyor. Bunu iki komşu elemandan bulalım: \(-108\) elde etmek için \(324\)'ü neyle çarpmamız gerekiyor?
\(324·q=-108\)	Buradan paydayı kolayca hesaplayabiliriz.
\(q=-\) \(\frac(108)(324)\) \(=-\) \(\frac(1)(3)\)	Artık ihtiyacımız olan öğeyi kolayca bulabiliriz.
	Cevap hazır.

Cevap : \(4\).

Örnek: İlerleme \(b_n=0.8·5^n\) koşuluyla belirtilir. Hangi sayı bu ilerlemenin üyesidir:

a) \(-5\) b) \(100\) c) \(25\) d) \(0,8\) ?

Çözüm: Görevin ifadesinden bu rakamlardan birinin kesinlikle ilerlememizde olduğu açıktır. Bu nedenle ihtiyacımız olan değeri bulana kadar terimlerini tek tek hesaplayabiliriz. İlerlememiz formülle verildiğinden, elemanların değerlerini farklı \(n\) yerine koyarak hesaplıyoruz:
\(n=1\); \(b_1=0.8·5^1=0.8·5=4\) – listede böyle bir sayı yok. Devam edelim.
\(n=2\); \(b_2=0.8·5^2=0.8·25=20\) - ve bu da orada değil.
\(n=3\); \(b_3=0.8·5^3=0.8·125=100\) – ve işte şampiyonumuz!

Cevap: \(100\).

Örnek (OGE): Geometrik ilerlemenin birkaç ardışık terimi verilmiştir...\(8\); \(X\); \(50\); \(-125\)…. \(x\) etiketli elemanın değerini bulun.

Çözüm:

Cevap: \(-20\).

Örnek (OGE): İlerleme \(b_1=7\), \(b_(n+1)=2b_n\) koşullarıyla belirtilir. Bu ilerlemenin ilk \(4\) teriminin toplamını bulun.

Çözüm:

Cevap: \(105\).

Örnek (OGE): Geometrik ilerlemede \(b_6=-11\), \(b_9=704\) olduğu bilinmektedir. Paydayı \(q\) bulun.

Çözüm:

	Soldaki şemada \(b_6\)'dan \(b_9\)'a "ulaşmak" için üç "adım" attığımızı, yani \(b_6\)'yı paydayla üç kez çarptığımızı görebilirsiniz. ilerlemenin. Başka bir deyişle, \(b_9=b_6·q·q·q=b_6·q^3\).
\(b_9=b_6·q^3\)	Bildiğimiz değerleri yerine koyalım.
\(704=(-11)q^3\)	Denklemi ters çevirelim ve \((-11)\)'e bölelim.
\(q^3=\) \(\frac(704)(-11)\) \(\:\:\: ⇔ \:\:\: \)\(q^3=-\) \(64 \)	Hangi sayının küpü \(-64\) verir? Elbette \(-4\)!
	Cevap bulundu. Sayı zincirini \(-11\)'den \(704\)'e geri yükleyerek kontrol edilebilir.
	Her şey bir araya geldi - cevap doğru.

Cevap: \(-4\).

En önemli formüller

Gördüğünüz gibi, geometrik ilerleme problemlerinin çoğu saf mantık kullanılarak, yalnızca özün anlaşılmasıyla çözülebilir (bu genellikle matematik için tipiktir). Ancak bazen belirli formüllerin ve kalıpların bilinmesi çözümü hızlandırır ve önemli ölçüde kolaylaştırır. Bu tür iki formülü inceleyeceğiz.

\(n\)'inci terimin formülü: \(b_n=b_1·q^(n-1)\), burada \(b_1\) ilerlemenin ilk terimidir; \(n\) – gerekli öğenin numarası; \(q\) – ilerleme paydası; \(b_n\) – \(n\) sayısıyla ilerlemenin terimi.

Bu formülü kullanarak, örneğin ilk örnekteki sorunu tam anlamıyla tek bir eylemle çözebilirsiniz.

Örnek (OGE): Geometrik ilerleme \(b_1=-2\) koşullarıyla belirtilir; \(q=7\). \(b_4\) bulun.
Çözüm:

Cevap: \(-686\).

Bu örnek basitti, dolayısıyla formül hesaplamaları bizim için çok fazla kolaylaştırmadı. Soruna biraz daha karmaşık bakalım.

Örnek: Geometrik ilerleme \(b_1=20480\) koşullarıyla belirtilir; \(q=\frac(1)(2)\). \(b_(12)\)'yi bulun.
Çözüm:

Cevap: \(10\).

Elbette, \(\frac(1)(2)\)'i \(11\)'inci kuvvete yükseltmek pek keyifli değil, ama yine de \(11\)'in \(20480\)'i ikiye bölmesinden daha kolaydır.

İlk terimlerin toplamı \(n\): \(S_n=\)\(\frac(b_1·(q^n-1))(q-1)\) , burada \(b_1\) ilk terimdir ilerlemenin; \(n\) – toplanan öğelerin sayısı; \(q\) – ilerleme paydası; \(S_n\) – ilerlemenin \(n\) ilk terimlerinin toplamı.

Örnek (OGE): Paydası \(5\) ve ilk terimi \(b_1=\frac(2)(5)\) olan geometrik bir ilerleme \(b_n\) verildiğinde. Bu ilerlemenin ilk altı teriminin toplamını bulun.
Çözüm:

Cevap: \(1562,4\).

Ve yine, sorunu doğrudan çözebiliriz; altı öğenin tümünü sırayla bulabilir ve ardından sonuçları ekleyebiliriz. Ancak hesaplamaların sayısı ve dolayısıyla rastgele hata olasılığı keskin bir şekilde artacaktır.

Geometrik ilerleme için, pratik kullanımlarının düşük olması nedeniyle burada dikkate almadığımız birkaç formül daha vardır. Bu formülleri bulabilirsiniz.

Geometrik ilerlemelerin arttırılması ve azaltılması

Makalenin başında ele alınan \(b_n = \(3; 6; 12; 24; 48...\)\) ilerlemesi için payda \(q\) birden büyüktür ve dolayısıyla her sonraki terim öncekinden daha büyüktür. Bu tür ilerlemelere denir artan.

Eğer \(q\) birden küçükse ancak pozitifse (yani sıfırdan bire kadar olan aralıkta yer alıyorsa), o zaman sonraki her öğe bir öncekinden daha küçük olacaktır. Örneğin ilerlemede \(4\); \(2\); \(1\); \(0,5\); \(0,25\)... \(q\)'nin paydası \(\frac(1)(2)\)'a eşittir.

Bu ilerlemelere denir azalan. Böyle bir ilerlemenin hiçbir unsurunun olumsuz olmayacağını, yalnızca her adımda küçüldüklerini unutmayın. Yani yavaş yavaş sıfıra yaklaşacağız ama asla ulaşamayacağız ve ötesine geçemeyeceğiz. Bu gibi durumlarda matematikçiler “sıfıra eğilim gösterir” derler.

Negatif bir payda ile geometrik ilerlemenin elemanlarının mutlaka işaret değiştireceğini unutmayın. Örneğin, y ilerlemesi \(5\); \(-15\); \(45\); \(-135\); \(675\)... \(q\)'nın paydası \(-3\)'tir ve bu nedenle elementlerin işaretleri “yanıp söner”.